Перечислите способы задания дискретной случайной величины

Перечислите способы задания дискретной случайной величины

Случайной называется величина, которая в результате испытания может принять то или иное числовое значение, причем заранее неизвестно, какое именно.

Если для какой- либо величины ее измерение повторять многократно в практически одинаковых условиях, то обнаружится, что всякий раз получаются несколько отличные друг от друга результаты. Это складывается влияние причин двух видов: 1) основных, определяющих главное значение результата; 2) второстепенных, обуславливающих их расхождение.

При совместном действии этих причин понятия необходимости и случайности оказываются тесно связанными между собой, но необходимое преобладает над случайным.

Таким образом, возможные значения случайных величин принадлежат некоторым числовым множествам.

Случайным является то, что на этих множествах величины могут принять любое значение, но какое именно, заранее сказать нельзя.

Случайная величина связана со случайным событием.

Если случайное событие — качественная характеристика испытаний, то случайная величина — его количественная характеристика.

Законы распределения могут быть заданы тремя способами: табличным, графическим, аналитическим. Способ задания зависит от типа случайной величины.

Различают два основных типа случайных величин: дискретные и непрерывно распределенные случайные величины.

Источник

Закон распределения вероятностей дискретной случайной величины

Дата добавления: 2013-12-23 ; просмотров: 7594 ; Нарушение авторских прав

Определение2.1:Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями.

Способы задания дискретной случайной величины

1) Для задания дискретной случайной величины достаточно задать семейство вероятностей p_i = P(X = x_i), где или .

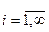
2) Табличный способ задания дискретной случайной величины: первая строка таблицы содержит возможные значения случайной величины, расположенные в порядке возрастания, а вторая – их вероятности:

X	x1	x2	x3	…..	xn
P	p1	p2	p3	…..	pn

Сумма вероятностей второй строки таблицы равна единице:

(условие нормировки).

Замечание1: В одном испытании случайная величина X принимает одно и только одно возможное значение, следовательно, события (X = x_i), где образуют полную группу.

Замечание2: Если множество возможных значений бесконечно (счетно), то ряд 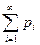сходится и его сумма равна единице.

3) Многоугольник распределения или графический способ задания дискретной случайной величины.

В прямоугольной системе координат строят точки ( x_i , p_i ), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

4) Задать закон распределения дискретной случайной величины можно в виде функции распределения вероятностей (интегральной функции распределения) F(x).

Пример.В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 10000 рублей и десять выигрышей по 1000 рублей. Найти ряд распределения, функцию распределения случайной величины X – стоимости возможного выигрыша для владельца одного лотерейного билета. Построить многоугольник распределения.

Решение: Случайная величина X принимает значения 0,1000,10000с вероятностями:

, , .Таким образом, ряд распределения имеет следующий вид:

X
P	0,89	0,1	0,01

Условие нормировки выполняется: .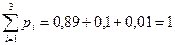

Источник

Способы задания случайных величин

Основные распределения

Случайных величин

Методические указания для самостоятельной работы студентов

всех форм обучения

Составитель В.А. Бобкова

Составитель В.А. Бобкова

Основные распределения случайных величин: Методические указания для самостоятельной работы студентов всех форм обучения/ Сост. В. А. Бобкова; ГОУВПО Иван. гос. хим.-технол. ун-т. – Иваново, 2005. 32 с.

Методические указания посвящены одному из важных разделов курса «Теория вероятностей и математическая статистика», а именно: основным распределениям случайных величин. Дано понятие случайной величины, описаны способы задания дискретных и непрерывных случайных величин, приведены определения математического ожидания, дисперсии, среднеквадратического отклонения. Далее рассмотрены основные распределения дискретных случайных величин: распределение Бернулли, биномиальное распределение, распределение Пуассона, геометрическое и гипергеометрическое распределения, а также основные распределения непрерывных случайных величин: равномерное, показательное, нормальное распределения. Выведены формулы для числовых характеристик рассмотренных распределений, приведены графические иллюстрации и примеры решения задач. Даны задачи для самостоятельного решения.

Методические указания предназначены для самостоятельной работы студентов всех специальностей вуза.

Библиогр.: 4 назв.

Рецензент доктор технических наук, профессор А. Н. Лабутин

(Ивановский государственный химико-технологический университет)

Основные сведения о случайных величинах

Понятие случайной величины

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, заранее не известное и зависящее от случайных причин, которые не могут быть учтены.

Случайные величины обозначаются прописными латинскими буквами X,Y, Z, …, а их возможные значения – соответствующими строчными буквами x, y, z, … .

Примеры случайных величин:

1) число вызовов, поступивших от абонентов на телефонную станцию в течение определённого времени;

2) вес наугад взятого зерна пшеницы;

3) число отличных оценок у студентов одной группы на экзамене;

4) расстояние от точки метания диска до точки падения;

5) число опечаток в книге.

Разнообразие случайных величин велико. Число принимаемых ими значений может быть конечным, счётным или несчетным; эти значения могут быть расположены дискретно или заполнять интервалы (конечные или бесконечные).

Дискретные случайные величины – это случайные величины, которые могут принимать только конечное или счетное множество значений. Например, число появлений герба при пяти подбрасываниях монеты (возможные значения 0, 1, 2, 3, 4, 5); число выстрелов до первого попадания в цель (возможные значения 1, 2, … , n, где n – число имеющихся в наличии патронов); число отказавших элементов в приборе, состоящем из трех элементов (возможные значения 0, 1, 2, 3) – это дискретные случайные величины.

Непрерывные случайные величины – это случайные величины, возможные значения которых образуют некоторый конечный или бесконечный интервал. Например, время безотказной работы прибора, дальность полёта снаряда, время ожидания автобуса – это непрерывные случайные величины.

Способы задания случайных величин

Для того, чтобы задать случайную величину, надо знать те значения, которые она может принимать, и вероятности, с которыми случайная величина принимает свои значения. Любое правило (таблица, функция, график), позволяющее находить вероятности отдельных значений случайной величины или множества этих значений, называется законом распределения случайной величины (или просто распределением). Про случайную величину говорят, что «она подчиняется данному закону распределения».

Пусть X –дискретная случайная величина, которая принимает значения (множество этих значений конечно или счетно) с некоторыми вероятностями . Закон распределения дискретной случайной величины удобно задавать с помощью формулы i = 1, 2, 3, … , n, … , определяющей вероятность того, что в результате опыта случайная величина X примет значение . Для дискретной случайной величины закон распределения может быть задан в виде таблицы распределения:

X			…		…
P			…	pn	…

Здесь первая строка содержит все возможные значения (обычно в порядке возрастания) случайной величины, а вторая – их вероятности. Такую таблицу называют рядом распределения.

Так как события несовместны и образуют полную группу событий, то сумма их вероятностей равна единице.

Закон распределения дискретной случайной величины можно задать графически, если на оси абсцисс отложить возможные значения случайной величины, а на оси ординат – их вероятности. Ломаную, соединяющую последовательно полученные точки, называют многоугольником распределения.

Очевидно, что ряд распределения можно построить только для дискретных случайных величин. Для непрерывных случайных величин нельзя даже перечислить все возможные значения.

Универсальным способом задания закона распределения вероятностей, пригодным как для дискретных, так и для непрерывных случайных величин, является её функция распределения.

Пусть Х – случайная величина, х — действительное число. Функцией распределения вероятностей случайной величины Х называют вероятность того, что эта случайная величина примет значение, меньшее, чем х:

(1)

Геометрически это равенство можно истолковать так: F(x) есть вероятность того, что случайная величина X примет значение, которое изображается на числовой оси точкой, лежащей левее точки x, то есть что случайная точка X попадёт в интервал .

Свойства функции распределения:

1. Значения функции распределения принадлежат отрезку [0,1]:

(2)

2. F(x) – неубывающая функция, то есть если .

Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале [a,b), равна приращению функции распределения на этом интервале:

(3)

Следствие 2. Вероятность того, что непрерывная случайная величина примет одно определенное значение, равна нулю.

3. Если возможные значения случайной величины принадлежат интервалу (a,b), то при и при .

Следствие. Если возможные значения непрерывной случайной величины расположены на всей оси x, то справедливы следующие предельные соотношения:

(4)

Непрерывную случайную величину можно также задать, используя другую функцию, которую называют плотностью распределения или плотностью вероятности.

Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f(x) – первую производную от функции распределения F(x):

. (5)

Из этого определения следует, что функция распределения является первообразной для плотности распределения.

Заметим, что для описания распределения вероятностей дискретной случайной величины плотность распределения неприменима.

Свойства плотности распределения:

1. Плотность распределения является неотрицательной функцией: для любого x. Это свойство следует из того, что функция распределения F(x) – неубывающая функция.

2. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a,b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b:

. (6)

Геометрически это можно истолковать так: вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a,b), равна площади криволинейной трапеции, ограниченной осью Ox, кривой распределения f(x) и прямыми x = a и x = b (см. рис.1).

Рис. 1. График плотности распределения непрерывной случайной величины. Площадь S равна вероятности попадания случайной величины в интервал (a,b).

Следствие 1. Несобственный интеграл от плотности распределения в пределах от до равен единице:

(7)

Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью Ox и кривой распределения, равна единице (см. рис. 2).

Рис. 2. Площадь под графиком интегральной кривой равна единице.

Следствие 2. Зная плотность распределения f(x), можно найти функцию распределения F(x) по формуле:

. (8)

Действительно, если в формуле (6) перейти к пределу при ; то . Следовательно, . Отсюда получается выражение (8) для F(x).

Итак, для того, чтобы некоторая функция была плотностью вероятностей, должны выполняться следующие условия:

а) функция должна быть неотрицательной;

б) должно выполняться равенство ;

в) функция должна стремиться к 0 при .

Источник