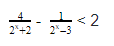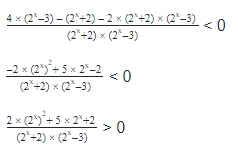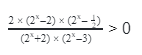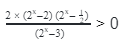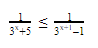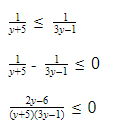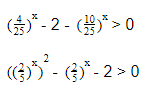- Методы решения показательных неравенств
- Показательные неравенства (ЕГЭ 2022)
- Показательные неравенства — коротко о главном
- Метод интервалов
- Читать далее…
- Показательные неравенства
- Определение показательных неравенств
- Как решать показательные неравенства
- Показательные неравенства, сводящиеся к простейшим
- Пример 1
- Показательные неравенства, сводящиеся к квадратным
- Пример 1
- Показательные неравенства, сводящиеся к рациональным
- Пример 1
- Пример 2
- Однородные показательные неравенства
- Пример 1
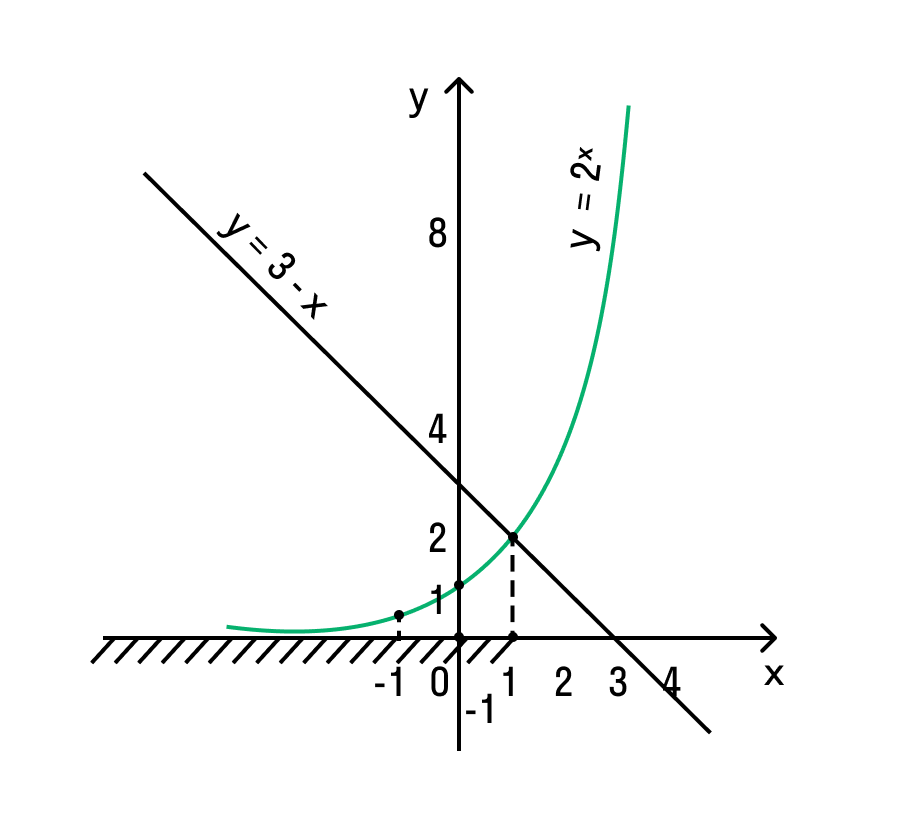
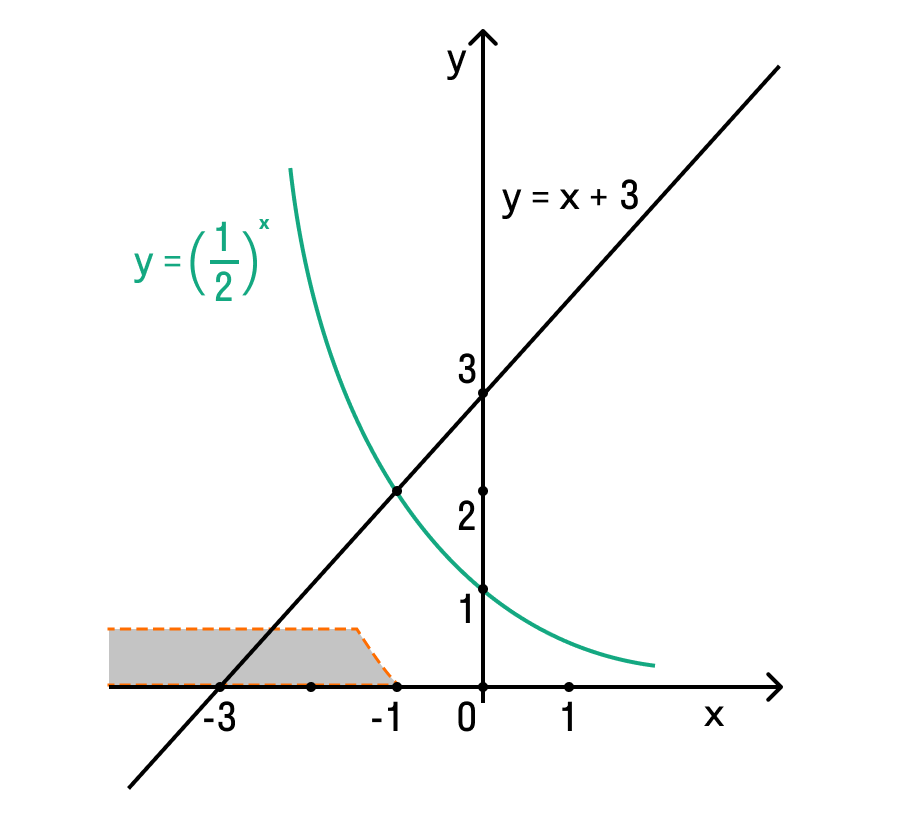
- Неравенства, решаемые графическим методом
- Пример 1
- Пример 2
Методы решения показательных неравенств
Разделы: Математика
В работе изложены методы решения показательных неравенств, как простейших, так и более сложных, решение которых сводится к решению простейших неравенств. Среди предложенных методов – метод уравнивания оснований, метод разложения на множители, метод введения новой переменной, графический метод и другие. К каждому методу дано краткое описание и решение 1-2 примеров, иллюстрирующих данный метод. Имеются задания двух уровней А и В для самоконтроля по вышеуказанной теме.
Показательным неравенством называется неравенство, в котором переменная содержится в показателе степени.
Решение простейших показательных неравенств основано на свойстве возрастания (убывания) показательной функции: если основание показательной функции больше единицы, то показательная функция возрастает на R , то есть большему значению функции соответствует большее значение аргумента, а меньшему значению функции соответствует меньшее значение аргумента.
Если основание показательной функции больше нуля, но меньше единицы, то показательная функция убывает на R, то есть большему значению функции соответствует меньшее значение аргумента, а меньшему значению функции соответствует большее значение аргумента.
- Простейшие неравенства (Приложение 1).
- Методы решения произвольных показательных неравенств (Приложение 2).
- Практические задания для самоконтроля (Приложение 3).
Источник
Показательные неравенства (ЕГЭ 2022)
В этой статье есть все о показательных неравенствах.
Для тех, кто ничего не знает, мы начнем с самых азов, с самых простейших примеров. И постепенно научим вам решать любые показательные неравенства, которые могут встретиться вам на ЕГЭ.
Если вы продвинутый школьник, вы можете пропустить азы и переходить сразу… к методу декомпозиции или к анализу монотонности функций. 🙂
А если серьезно, даже если вы уже хорошо знаете тему, вы точно найдете для себя что-то новое!
Или же хорошо потренируетесь, если решите все 44 неравенства этой статьи самостоятельно.
Показательные неравенства — коротко о главном
Определение:
Простейшими показательными неравенствами являются неравенства следующего вида:
\(<^
f\left( x \right)>g\left( x \right)\) \(\left(при\
f\left( x \right) 25\), каким же должен быть \(\displaystyle x\)?
Я думаю, что ты без труда понял, что \(\displaystyle x>5\).
А если \(\displaystyle <<5>^
Так как \(\displaystyle 25=<<5>^<2>>\), то ты вполне резонно можешь предположить, что \(\displaystyle x>2\).
А вот пример позабористее: \(\displaystyle <<0,1>^
Опять таки, легко сосчитать, что \(\displaystyle 0,01=<<0,1>^<2>>\). И у нас получится \(\displaystyle <<0,1>^
И какой можно из этого сделать вывод? Может быть, как и в предыдущем примере, \(\displaystyle x>2\)?
На первый взгляд, это кажется вполне очевидным. Но, увы, это не правильно.
Потому что, как ни парадоксально, из \(\displaystyle <<0,1>^
><<0,1>^<2>>\) следует, что \(\displaystyle x
Кратко это правило можно записать так:
Такие же правила ты можешь получить для трех оставшихся знаков неравенств: \(\displaystyle -2\)?
- во-первых, не принято и не умеют решать показательные неравенства в которых \(\displaystyle a=1\) потому, что сколько единицу не умножай саму на себя (а именно это и делает степень), ничего кроме самой единицы ты все равно не получишь.
- То же самое касается и неравенств, в которых основание меньше нуля — просто забудь о них.
- Отдельного разговора (и абзаца) заслуживает последний случай.
Давай вместо основания возьмем число \(\displaystyle 2\) и будем возводить его во всевозможные степени:
| \(\displaystyle n\) | \(\displaystyle 0\) | \(\displaystyle 1\) | \(\displaystyle -1\) | \(\displaystyle 2\) | \(\displaystyle -2\) | \(\displaystyle 3\) | \(\displaystyle -3\) | \(\displaystyle 4\) | \(\displaystyle -4\) |
| \(\displaystyle <<2>^ | \(\displaystyle 1\) | \(\displaystyle 2\) | \(\displaystyle \frac<1><2>\) | \(\displaystyle 4\) | \(\displaystyle \frac<1><4>\) | \(\displaystyle 8\) | \(\displaystyle \frac<1><8>\) | \(\displaystyle 16\) | \(\displaystyle \frac<1><16>\) |
Ты понял, как я заполнил эту таблицу? Нет!?
Стыд и позор, я же просил повторить свойства степени. Вернись и перечитай, а потом возвращайся к нам.
Итак, все стало понятно? Ну что же, продолжим.
Что мы видим в этой таблице?
Чем больше степень, тем больше значение выражения \(\displaystyle <<2>^
>\), и наоборот: чем меньше степень, тем это значение меньше.
Но, тем не менее, видно что, \(\displaystyle <<2>^
>\) всегда больше нуля.
ВСЕГДА. Это же свойство справедливо ДЛЯ ЛЮБОГО ОСНОВАНИЯ С ЛЮБЫМ ПОКАЗАТЕЛЕМ!!
Решил? Честно? Ну хорошо, давай проверять вместе:
Пример 1. \(\displaystyle <<2>^
\(\displaystyle x+2\le 3\), откуда \(\displaystyle x\le 1\),
\(\displaystyle x\in \left( -\infty ;1 \right]\).
Пример 3. \(\displaystyle <<27>^
Продолжаем нагромождать: в третьем примере нас ждет беда: так получилось, что \(\displaystyle 81\) это не целая степень числа \(\displaystyle 27\), (в чем несложно убедиться, возводя число \(\displaystyle 81\) в различные целые степени \(\displaystyle 0\), \(\displaystyle 1\), \(\displaystyle -1\)…).
И что же теперь делать? Бросать решение примера?
Нет! Этого не одобрю ни я, ни твой школьный учитель по математике.
Давай немного напряжемся и заметим, что и \(\displaystyle 27\) и \(\displaystyle 81\) это степени одного и того же числа. Какого? Конечно, это степени тройки (\(\displaystyle 27=<<3>^<3>>,
Тогда все становится сразу понятным:
\(\displaystyle <<27>^
\(\displaystyle <<3>^<3\left( x+2 \right)>>\le <<3>^<4>>\) (напомню, что при такой «замене» степени умножаются!).
Так как \(\displaystyle 3>1\), то знак неравенства не меняется и мы получаем:
\(\displaystyle 3\left( x+2 \right)\le 4\).
\(\displaystyle 3x+6\le 4,
Отсюда, ответ:
\(\displaystyle x\in \left( -\infty ;
Пример 4. Теперь мы решим еще более «навороченный» пример:
На самом деле, у нас есть аж два способа решить данное неравенство:
Во-первых, представить \(\displaystyle \frac<1><3>\) как \(\displaystyle <<3>^<-1>>\)
(Если для тебя это «превращение» показалось магическим, перечитай свойства степени с отрицательным показателем)
Либо представить \(\displaystyle 9\) как \(\displaystyle <<\left( \frac<1> <3>\right)>^<-2>>\).
Мне хочется сейчас пойти именно вторым путем, ну а ты сам можешь применить первый. Как ты понимаешь, ответы должны совпасть.
Теперь слева и справа в неравенстве мы имеем одинаковые основания, значит мы можем перейти к неравенству относительно их показателей.
Однако, можно (и нужно!) заметить, что \(\displaystyle \frac<1> <3>9\)
Ну что же, здесь все нам тоже более-менее знакомо, единственно, что нужно вспомнить, так это то, что \(\displaystyle \frac<1><\sqrt<5>>=\sqrt<\frac<1><5>>=<<\left( \frac<1> <5>\right)>^<\frac<1><2>>>\).
Теперь окончательно получим:
Опять-таки \(\displaystyle \left( \frac<1> <5>\right) \frac<1><2>:\left( -4 \right)\)
\(\displaystyle x>-\frac<1><8>\)
Нам осталось лишь записать полученный правильный ответ:
\(\displaystyle x\in \left( -\frac<1><8>;
Задачки для совсем самостоятельного решения:
\(\displaystyle <<3>^<-2x>> ты умеешь решать почти все показательные неравенства из первой части профильного ЕГЭ!
Но мы ведь с тобой хотим стать еще лучше и уметь решать еще более сложные неравенства?
Как ты без труда (или почти без труда) заметил, каждый раз, когда мы решали показательное неравенство, оно сводилось к некоторому линейному неравенству для показателей. Более того, каждая из частей (правая и левая) неравенства состояла ровно из одного выражения.
Что же запрещает природе вмешаться и сделать, например, с каждой стороны неравенства, скажем, не по одному выражению, а по три или даже четыре? Или же что ей запрещает составить такое неравенство, которое сводится уже не к линейному, а к квадратичному?
Правильно, ничего не запрещает. Поэтому мы должны быть готовы к решению и таких неравенств тоже. Давай вначале посмотрим на некоторые примеры:
Применим к нему уже знакомую не понаслышке технику. Что же мы получим в итоге?
Кто знает, что это такое? Конечно это квадратное неравенство! А теперь быстренько вспоминаем, как они решаются!
Да почти что как квадратные уравнения. А вот уж их ты точно умеешь решать, я не сомневаюсь.
Вычисляем дискриминант: \(\displaystyle D=<<\left( -5 \right)>^<2>>-4\cdot 1\cdot 6=1\)
Так как дискриминант больше нуля, то уравнение имеет два корня:
Если бы мы решали уравнение, то на этом можно было бы и остановиться. Но у нас с тобой более «высокая цель» – решение неравенства.
Поэтому далее нам нужен метод интервалов.
Метод интервалов
Метод интервалов — самый универсальный способ решения неравенств. Но он особенно эффективен при решении квадратных неравенств.
В этом разделе разберем алгоритм решения квадратных неравенств с помощью метода интервалов. И конечно же решим пару-тройку примеров.
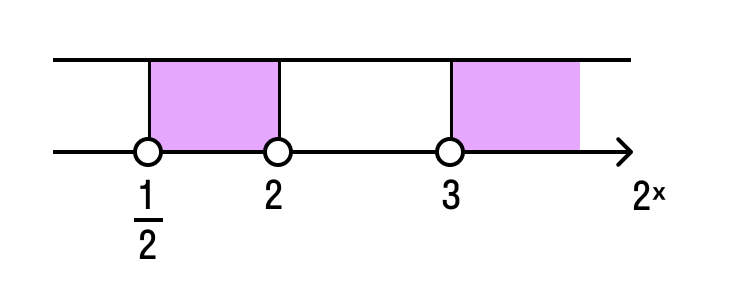
Отметим эти точки на координатной прямой и разделим эту прямую на три интервала, затем выберем какое-нибудь число в любом из интервалов и вычислим, чему равно наше исходное выражение \(\displaystyle <
Мне нравится брать такое число, чтобы нужно было как можно меньше считать. Догадался, какое же это число? Верно, это ноль.
Ноль принадлежит самому левому интервалу.
Наше выражение, если подставить в него ноль вместо икса, будет равно \(\displaystyle 6\), \(\displaystyle 6>0\).
Поэтому в левом интервале я ставлю знак \(\displaystyle +\). Далее чередую.
Поскольку мы решаем неравенство \(\displaystyle <
Таким образом, наш ответ будет:
\(\displaystyle x\in \left( -\infty ;2 \right)\mathop<\cup >^<>\left( 3;+\infty \right)\).
Теперь мне кажется, что ты без особого труда решишь следующие примеры:
Давай сверяться вместе:
Пример 1. \(\displaystyle <<\left( \frac<13> <11>\right)>^<<
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Источник
Показательные неравенства
О чем эта статья:
10 класс, 11 класс, ЕГЭ/ОГЭ
Определение показательных неравенств
Показательными считаются неравенства, которые включают в себя показательную функцию. Другими словами, это неравенства с переменной в показателе степени: a f(x) > a g(x) , a f(x) g(x) .
Из них показательно-степенными неравенствами являются те, в которых есть переменные и в показателе степени, и в основании.
Для изучения этой темы стоит повторить:
И, конечно, для решения тригонометрических и логарифмических показательных неравенств также придется вспомнить формулы соответствующих разделов алгебры.
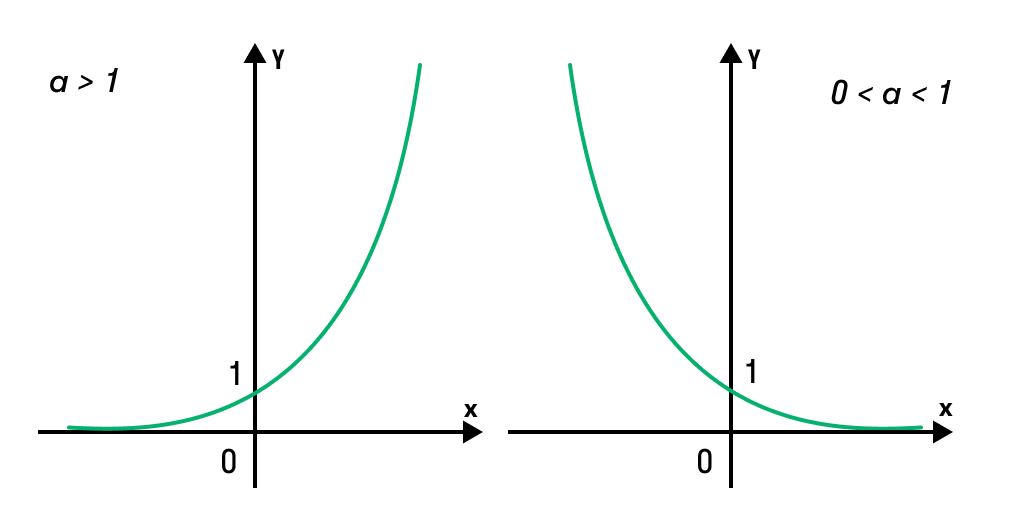
Если все это еще свежо в памяти, давайте приступим. Как и к показательным уравнениям, к неравенствам стоит подходить, помня о свойствах показательной функции. Напомним, что она выглядит так: y = a x , где a > 0 и a ≠ 1. Два графика ниже дают представление о том, на что похожа такая функция, когда основание степени а больше и меньше единицы. Наверняка вы уже догадались, каково главное свойство этой функции. Да, она монотонна.
При этом заметьте — значения а всегда больше нуля. На практике в этом несложно убедиться, если возводить какое-либо число во всевозможные степени, включая отрицательные. Например: 2 -2 = 4, 2 -4 = 1/16 и т. д. Значение функции будет уменьшаться, но никогда не достигнет нуля.
Для любых а и х верно неравенство a x > 0, т. е. показательная функция не принимает отрицательных значений.
Запишем следствие монотонности показательной функции в виде формул:
- a f(x) > a g(x) f(x) > g (x), когда функция возрастает, т. е. а > 1;
- a f(x) > a g(x) f(x)
Как решать показательные неравенства
Как мы уже говорили, для успешного освоения этой темы нужно хорошенько повторить все, что касается показательных уравнений. Способы решения показательных неравенств выглядят примерно так же — мы будем пытаться упростить выражение, получить одинаковые степени или одинаковые основания, по возможности свести все к квадратному или рациональному уравнению. Но есть и свои тонкости.
Допустим, у нас есть простейшее показательное неравенство:
Если вы помните, как решались показательные уравнения, не придется долго думать, что делать с таким неравенством — приведем его к одинаковому основанию:
Казалось бы, все логично, но всегда ли можно смело вычеркивать одинаковые основания степеней? А что, если вместо 3 у нас основание степени будет 0,5? Посмотрим:
Проверим, верно ли в таком случае х > 2.
0,5 3 = 0, 125 и т. д.
Как видите, на самом деле в этом случае х