Булевы функции

Содержание

1 Понятие булевой функции

В курсе математического анализа изучаются функции, определённые на числовой прямой или на отрезке числовой прямой или на (гипер-) плоскости и т.п. Так или иначе область определения – непрерывное множество. В курсе дискретной математики изучаться должны функции, область определения которых – дискретное множество * . Простейшим (но нетривиальным) таким множеством является множество, состоящее из двух элементов. * Так мы и приходим к понятию булевой функции.

Определение 1 (Булева функция). Булевой функцией от n аргументов называется функция f из n -ой степени множества < 0, 1 >в множество < 0, 1 >.

Иначе говоря, булева функция – это функция, и аргументы и значение которой принадлежит множеству < 0, 1 >. Множество < 0, 1 >мы будем в дальнейшем обозначать через B .

Булеву функцию от n аргументов можно рассматривать как n -местную алгебраическую операцию на множестве B . При этом алгебра W >, где W – множество всевозможных булевых функций, называется алгеброй логики .

Конечность области определения функции имеет важное преимущество – такие функции можно задавать перечислением значений при различных значениях аргументов. Для того, чтобы задать значение функции от n переменных, надо определить значения для каждого из 2 n наборов. Эти значения записывают в таблицу в порядке соответствующих двоичных чисел. В результате получается таблица следующего вида:

x 1	x 2	.	x n- 1	x n	f
0	0	.	0	0	f(0,0. 0,0)
0	0	.	0	1	f(0,0. 0,1)
0	0	.	1	0	f(0,0. 1,0)
0	0	.	1	1	f(0,0. 1,1)
.	.	.	.	.	.
1	1	.	0	0	f(1,1. 0,0)
1	1	.	0	1	f(1,1. 0,1)
1	1	.	1	0	f(1,1. 1,0)
1	1	.	1	1	f(1,1. 1,1)

Раз у нас есть стандартный порядок записывания наборов, то для того, чтобы задать функцию, нам достаточно выписать значения f (0,0. 0,0) , f (0,0. 0,1) , f (0,0. 1,0) , f (0,0. 1,1). f (1,1. 0,0) , f (1,1. 0,1) , f (1,1. 1,0) , f (1,1. 1,1). Этот набор называют вектором значений функции .

Таким образом, различных функций n переменных столько, сколько различных двоичных наборов длины 2 n * . А их 2 в степени 2 n .

Множество B содержит два элемента – их можно рассматривать как булевы функции от нуля (пустого множества) переменных – константу 0 и константу 1 .

Функций от одной переменной четыре: это константа 0, константа 1, тождественная функция , т.е. функция, значение которой совпадает с аргументом и так называемая функция « отрицание ». Отрицание будем обозначать символом ¬ как унарную операцию. Приведём таблицы этих четырёх функций:

x	0	x	¬ x	1
0	0	0	1	1
1	0	1	0	1

Как видим, функции от некоторого числа переменных можно рассматривать как функции от большего числа переменных. При этом значения функции не меняется при изменении этих «добавочных» переменных. Такие переменные называются фиктивными , в отличие от остальных – существенных .

Определение 2 (Фиктивные и существенные переменные). Переменная x i называется фиктивной (несущественной) переменной функции f ( x 1 ,···,x n ), если f ( x 1 ,···,x i- 1 ,0 ,x i+ 1 ,···,x n ) = f ( x 1 ,···,x i- 1 ,1 ,x i+ 1 ,···,x n ) для любых значений x 1 ,···,x i- 1 ,x i+ 1 ,···,x n . Иначе переменная x i называется существенной .

Функций от двух аргументов шестнадцать. Наиболее употребимые из этих функций (только те, которые существенно зависят от обеих переменных) мы приводим в следующей таблице:

x 1	x 2	x 1 & x 2	x 1 Ъ x 2	x 1 Й x 2	x 1 Е x 2	x 1 є x 2	x 1 | x 2
0	0	0	0	1	0	1	0
0	1	0	1	1	1	0	1
1	0	0	1	0	1	0	1
1	1	1	1	1	0	1	1

Эти функции записываются как бинарные операции в инфиксной нотации. x 1 & x 2 называется конъюнкцией , x 1 Ъ x 2 – дизъюнкцией , x 1 Й x 2 – импликацией , x 1 є x 2 – эквивалентностью , x 1 Е x 2 – суммой по модулю 2 , x 1 | x 2 – штрихом Шеффера .

Значения 0 и 1 часто интерпретируют как «ложь» и «истину». Тогда понятным становится название функции «отрицание» – она меняет «ложь» на «истину», а «истину» на «ложь». Отрицание читается как «не». Конъюнкция читается обычно как «и» – действительно, конъюнкция равна 1 тогда и только тогда, когда равны 1 и первая и вторая переменная. * Кроме x 1 & x 2 часто используют обозначение x 1 Щ x 2 или x 1 · x 2 или x 1 x 2 или min( x 1 ,x 2 ). Дизъюнкция читается «или» – дизъюнкция равна 1 тогда и только тогда, когда равны 1 первая или вторая переменная. * Импликация выражает факт, что из x 1 следует x 2 . * Импликацию часто также обозначают x 1 ® x 2 .

2 Суперпозиция функций

Определение 3 (Суперпозиция функций). Суперпозицией булевых функций f 0 и f 1 . f n называется функция f ( x 1 . x m ) = f 0 ( g 1 ( x 1 . x m ) . g k ( x 1 . x m )), где каждая из функций g i ( x 1 , . x m ) либо совпадает с одной из переменных (тождественная функция), либо – с одной из функций f 1 . f n .

Пример 1 (суперпозиция функций).

Функция f ( x,y ) = ¬ ( x & y ) является суперпозицией функций ¬ и &. Функция g ( x,y ) = x Е ( x Ъ y ) является суперпозицией функций Е и Ъ . Функция h ( x,y,z ) = ( x & y ) Е z является суперпозицией функций Е и &. Построим таблицы этих функций.

Суперпозицию ( x & y ) Е ( ¬x Ъ ¬y ) можно прочитать как « x и y плюс не x или не y ».

Следующие соотношения могут быть проверены прямым сравнением значений функций в левой и правой части соотношения на всевозможных наборах аргументов.

1. x & y = y & x
2. x Ъ y = y Ъ x
3. x Е y = y Е x
4. x & ( y & z ) = ( x & y ) & z
5. x Ъ ( y Ъ z ) = ( x Ъ y ) Ъ z
6. x Е ( y Е z ) = ( x Е y ) Е z
7. x Ъ ( y & z ) = ( x Ъ y ) & ( x Ъ z )
8. x & ( y Ъ z ) = ( x & y ) Ъ ( x & z )
9. ¬¬x = x
10. ¬ ( x & y ) = ¬x Ъ ¬y
11. ¬ ( x Ъ y ) = ¬x & ¬y
12. x & x = x
13. x & ¬x = 0
14. x & 0 = 0
15. x & 1 = x
16. x Ъ x = x
17. x Ъ ¬x = 1
18. x Ъ 0 = x
19. x Ъ 1 = 1
20. x Е y = ( x & ¬y ) Ъ ( ¬x & y )
21. x Й y = ¬x Ъ y
22. x є y = ( x & y ) Ъ ( ¬x & ¬y )

3 Двойственные функции

Определение 4 (Двойственная функция). Функция g ( x 1 . x n ) = ¬f ( ¬x 1 . ¬x n ) называется двойственной функцией к функции f и обозначается f * .

Пример 2 (двойственные функции).

( x & y ) * = ¬ ( ¬x & ¬y ) = x Ъ y .

Предложение 1 (Двойственная к двойственной функции). Функция, двойственная к двойственной функции f равна самой функции f.

Доказательство. f * ( x 1 . x n ) * = ( ¬f ( ¬x 1 . ¬x n )) * = *
= ¬¬f ( ¬¬x 1 . ¬¬x n ) = *
= f ( x 1 . x n ) *

Рассмотрим, что происходит с таблицей двойственной функции. Замена набора ( x 1 . x n ) на ( ¬x 1 . ¬x n ) соответствует «переворачиванию» таблицы. Действительно, наборы ( x 1 . x n ) и ( ¬x 1 . ¬x n ) расположены симметрично относительно середины таблицы. Теперь остаётся применить операцию ¬ к результату функции, т.е. поменять 0 на 1 и 1 на 0. Т.о. вектор значений функции, двойственной к исходной, получается из вектора исходной функции переворачиванием и заменой 0 на 1, а 1 на 0.

Пример 3 (вектор двойственной функции).

Функции x & y и x Ъ y , задаваемые векторами значений (0,0,0,1) и (0,1,1,1) двойственны друг к другу. Также двойственными являются x Е y и x є y , задаваемые векторами (0,1,1,0) и (1,0,0,1). Каждая из функций x и ¬x (векторы (0,1) и (1,0) соответственно) двойственна сама себе.

Теорема 1 (Принцип двойственности). Функция, двойственная к суперпозиции функций, равна суперпозиции двойственных функций. Точнее: f 0 ( f 1 . f m ) * = f 0 * ( f 1 * . f m * )

Доказательство. f 0 ( f 1 ( x 1 . x n ) . f m ( x 1 . x n )) * =

= ¬f 0 ( f 1 ( ¬x 1 . ¬x n ) . f m ( ¬x 1 . ¬x n )) =	*
= ¬f 0 ( ¬¬f 1 ( ¬x 1 . ¬x n ) . ¬¬f m ( ¬x 1 . ¬x n )) =	*
= ¬f 0 ( ¬f 1 * ( x 1 . x n ) . ¬f m * ( x 1 . x n )) =	*
= f 0 * ( f 1 * ( x 1 . x n ) . f m * ( x 1 . x n ))	*

4 Разложение функции по переменным

x s =

м ¬x, если s =0 н о x, если s =1

.

Теорема 2 (Разложение в дизъюнкцию). Любую функцию f ( x 1 . x m ) для любого n (1 Ј n Ј m ) можно представить в виде f ( x 1 . x m ) = x 1 s 1 & . & x n s n & f ( s 1 . s n ,x n+ 1 . x m )

Доказательство. Покажем, что для любого набора значений переменных ( x 1 . x n ,x n+ 1 . x m ) значения левой и правой частей совпадают. Возьмём фиксированный набор ( x 1 . x n ,x n+ 1 . x m ). Рассмотрим выражение x 1 s 1 & . & x n s n . Если одно из значений x i s i равно 0, то и всё выражение равно 0. Тогда и выражение x 1 s 1 & . & x n s n & f ( s 1 . s n ,x n+ 1 . x m ) равно 0. Единице же выражение x 1 s 1 & . & x n s n равно только в том случае, если s 1 = x 1 , . s n = x n . При этом f ( s 1 . s n ,x n+ 1 . x m ) = f ( x 1 . x n ,x n+ 1 . x m ) Таким образом, значение правой части всегда равно равно f ( x 1 . x m ), то есть значению левой части.

Теорема 3 (Разложение в конъюнкцию). Любую функцию f ( x 1 . x m ) для любого n (1 Ј n Ј m ) можно представить в виде f ( x 1 . x m ) = x 1 ¬ s 1 Ъ . Ъ x n ¬ s n Ъ f ( s 1 . s n ,x n+ 1 . x m )

Разложения по всем переменным дают суперпозицию конъюнкции, дизъюнкции и отрицания.

Следствие 1 (Совершенная дизъюнктивная нормальная форма).

Любая функция f может быть представлена в следующей форме: *

f ( x 1 . x m ) = x 1 s 1 & . & x m s m & f ( s 1 . s m ) = *

= x 1 s 1 & . & x m s m

Следствие 2 (Совершенная конъюнктивная нормальная форма).

Любая функция f может быть представлена в следующей форме: * f ( x 1 . x m ) = x 1 ¬ s 1 Ъ . Ъ x m ¬ s m

Таким образом, любая булева функция может быть представлена суперпозицией конъюнкции, дизъюнкции и отрицания. Разложение по всем переменным в дизъюнкцию называется совершенной дизъюнктивной нормальной формой функции, а в конъюнкцию – совершенной конъюнктивной нормальной формой . *

Совершенная дизъюнктивная и конъюнктивная нормальная формы дают способ представления булевой функции через суперпозицию конъюнкции, дизъюнкции и отрицания если у нас есть таблица значений функции.

Чтобы получить совершенную дизъюнктивную нормальную форму, надо взять все наборы, на которых значение функции равно 1 и записать для каждого из них конъюнкцию переменных и их отрицаний. Если в наборе значение переменной 0 – то переменную надо взять с отрицанием, если 1 – без отрицания. Из получившихся конъюнкций надо построить дизъюнкцию.

Чтобы получить совершенную конъюнктивную нормальную форму, надо взять все наборы, на которых значение функции равно 0 и записать для каждого из них дизъюнкцию переменных и их отрицаний. Если в наборе значение переменной 0 – то переменную надо взять без отрицания, если 1 – с отрицанием. Из получившихся дизъюнкций надо построить конъюнкцию.

Пример 4 (совершенная дизъюнктивная нормальная форма).

Построим совершенную дизъюнктивную нормальную форму функции, заданной следующей таблицей.

x	y	z	f
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Наборы, на которых функция равна 1 – это (0,1,1), (1,0,1), (1,1,0), (1,1,1). Первый набор даёт конъюнкцию ¬x & y & z , второй – x & ¬y & z , третий – x & y & ¬z , четвёртый – x & y & z . В результате получаем ( ¬x & y & z ) Ъ ( x & ¬y & z ) Ъ ( x & y & ¬z ) Ъ ( x & y & z ).

Источник

Способы представления булевых функций

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ, МОЛОДЕЖИ И СПОРТА УКРАИНЫ

ЧЕРНИГОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ИНФОРМАЦИОННЫХ И КОМПЬЮТЕРНЫХ СИСТЕМ

ПРОЕКТИРОВАНИЕ ЭЛЕКТРОННЫХ УСТРОЙСТВ

Методические указания к расчетно-графическим работам

Компьютерная логика»

для студентов направлений подготовки
6.050102 «Компьютерные инженерия» и
6.050103 «Программная инженерия»

Обсуждено и рекомендовано

на заседании кафедры

информационных и компьютерных систем.

Чернигов ЧГТУ 2012

Проектування електронних пристроїв. Методичні вказівки до розрахунково-графічних робіт з дисципліни “Комп’ютерна логіка” для студентів напрямів підготовки 6.050102 «Комп’ютерна інженерія» та 6.050103 «Програмна інженерія» / Укладачі: Соломаха В.В., Гора Н.О. – Чернігів: ЧДТУ, 2012. — 97 с. Рос. мовою.

Составители: Соломаха Валерий Владимирович, старший преподаватель,

Гора Наталья Олеговна, старший преподаватель

Ответственный за выпуск:	Казимир В.В., зав. кафедрой информационных и компьютерных систем, доктор техн. наук, профессор
Рецензент:	Нестеренко С.О., канд. техн. наук, доцент

1 РГР №2. РЕАЛИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ НА ЛОГИЧЕСКИХ ЭЛЕМЕНТАХ. 6

1.1 Цель работы. 6

1.2 Теоретические сведения. 6

1.3 Способы представления булевых функций. 7

1.3.1 Табличный способ представления. 7

1.3.2 Матричный способ представления. 7

1.3.3 Графический способ представления. 8

1.3.4 Аналитический способ представления. 9

1.4 Логические функции. 9

1.4.1 Логические функции одной переменной. 9

1.4.2 Логические функции двух переменных. 9

1.5 Алгебра Буля. 10

1.6 Законы алгебры логики. 11

1.7 Переход от табличной формы представления. 12

1.8 Импликанты и имплициенты булевых функций. 13

1.9 Сокращенные, минимальные и тупиковые формы. 14

1.10 Метод карт Карно (диаграммы Вейча). 15

1.10.1 Минимизация функции трех переменных. 15

1.10.2 Минимизация функции четырех переменных. 16

1.10.3 Минимизация функции пяти переменных. 17

1.10.4 Минимизация систем булевых функций по картам Карно. 17

1.10 Алгебра Жегалкина. 19

1.11.1 Определение алгебры Жегалкина. 19

1.11.2 Преобразование функций в алгебре Жегалкина. 19

1.11.3 Переход от булевой алгебры к алгебре Жегалкина. 20

1.11 Задания, выполняемые в расчетно-графической работе. 21

1.12 Пример выполнения работы № 2. 23

1.13.1 Выполнение задания 1. 23

1.13.2 Выполнение задания 2. 27

1.13.3 Выполнение задания 3. 33

1.14 Содержание отчета. 34

2 РГР№3. ПРОЕКТИРОВАНИЕ И ИССЛЕДОВАНИЕ ТРИГГЕРОВ 35

2.1 Цель работы. 35

2.2 Теоретические сведения. 35

2.3 Запоминающие элементы триггеров. 38

3.3.1 Запоминающие элементы триггеров, управляемые уровнем тактирующего сигнала. 38

3.3.2 Запоминающие элементы триггеров, управляемые перепадом тактирующего сигнала. 43

— ЗЭЗЭ триггеров, собранные по MS схеме. 43

— ЗЭЗЭ по схеме трёх триггеров. 44

2.4 Задания, выполняемые в расчетно-графической работе. 46

2.5 Пример выполнения работы № 3. 47

3.5.1 Пример построения DV-триггеров по MS схеме на элементах И-НЕ 47

3.5.2 Пример реализации Т-триггера по MS схеме на элементах ИЛИ-НЕ 49

3.5.3 Пример реализации JK-триггера по схеме трех триггеров на И-НЕ 51

2.7 Содержание отчета. 53

3 РГР №4. ПРОЕКТИРОВАНИЕ И ИССЛЕДОВАНИЕ СИНХРОННЫХ АВТОМАТОВ. 54

3.1 Цель работы. 54

3.2 Теоретические сведения. 54

3.3 Абстрактный синтез автомата. 55

4.3.1 Минимизация числа состояний автомата 56

4.3.2 Кодирование состояний автомата. 59

4.3.3 Получение функций возбуждения блока памяти и функций выхода.. 61

3.4 Задания выполняемые в расчетно-графической работе. 61

3.5 Пример выполнения работы № 4. 63

3.7 Содержание отчета. 66

4 РЕКОМЕНДОВАННАЯ ЛИТЕРАТУРА. 67

ВВЕДЕНИЕ

Методические указания разработаны помощь в помощь для выполнения расчетно-графических работ по дисциплине «Компьютерная логика».

При изучении дисциплины выполняется три лабораторные работы

2.Реализация комбинационных схем на логических элементах.

3.Проектирование и исследование триггеров.

4.Проектирование синхронных цифровых автоматов.

При выполнении данных работ необходимо производить определенные расчеты, производить построение схем.

Все это и оформляется в виде соответствующих трех расчетно-графических работ по которым пишется и защищается отбельный отчет.

РГР №2. РЕАЛИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ НА ЛОГИЧЕСКИХ ЭЛЕМЕНТАХ

Цель работы

Изучить методы проектирования комбинационных схем на логических элементах типа И — НЕ, ИЛИ — НЕ, исключающее ИЛИ

Теоретические сведения

Функция F (x₁,x₂,…,x_n) называется логической или

булевой, если она принимает два значения: ложь или истина (0 или 1).

Аргументы x₁,x₂,…,x_n принимают так же значения ложь или истина (0 или 1) и называются также булевыми или логическими переменными.

ДЖОРДЖ БУЛЬ (George Boole)

2 ноября 1815 (Линкольн, Англия) –

8 декабря 1864 (Баллинтемпл,

Математика, Логика, Философия математики.

Один из основоположников математической логики.

Королевский колледж в Корке (Ирландия).

Упорядоченная совокупность переменных (x₁,x₂,…,x_n) называется булевым набором длины n.

Наборы, на которых функция F(x₁,x₂,…,x_n) = 0, называются нулевыми наборами, а на которых функция F(x₁,x₂,…,x_n) = 1, называются единичными наборами переменных.

Множество всех возможных двоичных наборов длины n называется областью определения булевой функции.

Множество значений функции на всех наборах называется областью значения логической функции

Булевая функция, определенная на всех двоичных наборах, называется полностью определенной, в противном случае – частично определенной логической функцией.

Способы представления булевых функций

1.3.1 Табличный способ представления

Таблица 1.1 – Функция четырех переменных

х1	х2	х3	х4	F
0	0	0	0	0
0	0	0	1	1
0	0	1	0	0
0	0	1	1	1
0	1	0	0	1
0	1	0	1	0
0	1	1	0	0
0	1	1	1	0
1	0	0	0	1
1	0	0	1	0
1	0	1	0	0
1	0	1	1	1
1	1	0	0	0
1	1	0	1	0
1	1	1	0	0
1	1	1	1	1

Такая таблица называется таблицей истинности.

Число двоичных наборов равно 2 n , где n – число переменных.

Наборы обозначаются десятичными или шестнадцатиричными числами: 2,4,7,8,9,10,15 или 2,4,7,8,9,A,F.

Недостаток: при увеличении числа переменных размер таблицы резко возрастает.

1.3.2 Матричный способ представления

Это — частный способ табличного представления логических функций. В частности – карты Карно.

Изобретены в 1952 Эдвардом В. Вейчем (диаграммы Вейча) и усовершенствованы в 1953 Морисом Карно(карты Карно).

Таблица 1.2 – Карта Карно четырех переменных

х3х4 х1х2	00	01	11	10
00	0	1	1	0
01	1	0	0	0
11	0	0	1	0
10	1	0	1	0

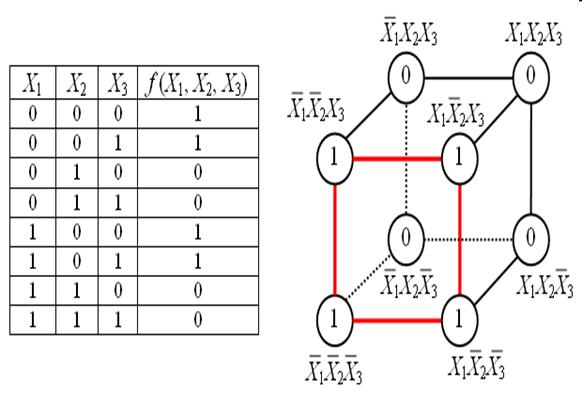
1.3.3 Графический способ представления

Логическая функция n переменных представляется n – мерным кубом, где каждый двоичный набор это n – мерный вектор, определяющий точку n – мерного пространства.

Рисунок 1.1 – Графическое представление функции трех переменных

1.3.4 Аналитический способ представления

Для этого вводится множество функций, а также правила зависимости функций от набора переменных, т.е. формулы – аналитические выражения на основе операций булевой алгебры.

Логические функции

1.4.1 Логические функции одной переменной

Количество логических функций в зависимости от числа переменных определяется следующим соотношением:

2 2 , т.к. функция и n аргументов принимают по 2 значения, т.е.

для одной переменной будет 4 функции:

Таблица 1.3 – Функции одной переменной

х	F0	F1	F2	F3
0	0	0	1	1
1	0	1	0	1

F₂ (х) = х – инверсия (отрицание);

1.4.2 Логические функции двух переменных

Таблица 1.4 – Функции двух переменных

х1	х2	F0	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	F12	F13	F14	F15
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
ù х2	х2®х1	ù х1	х1®х2	½	1

F₁ = х₁ Ù х₂ конъюнкция (логическое умножение), может обозначаться

F₂ = х₁ х₂ отрицание импликации (следования), может обозначаться

F₃ = х₁ тождественная функция первой переменной;

F₅ = х₂ тождественная функция второй переменной;;

F₁₀ = ù х₂ – отрицание (инверсия) х₂, может обозначаться ;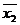

F₁₅ = 1 – константа единицы.

Алгебра Буля

Использует операции: дизъюнкцию, конъюнкцию, отрицание.

1. Ú—дизъюнкция — логическое сложение (операция „или”(or)):

Таблица 1.5 – Дизъюнкция

a	b	a Ú b
0	0	0
0	1	1
1	0	1
1	1	1

2. Ù — конъюнкция — логическое умножение (операция „и” (and)):

Таблица 1.6 – Конъюнкция

a	b	a Ù b
0	0	0
0	1	0
1	0	0
1	1	1

3.инверсия – отрицание (операция „не”)

Таблица 1.7 – Операция отрицание

а	ù а
0	1
1	0

Законы алгебры логики

1. Законы коммутативности:

2. Законы ассоциативности:

3. Законы дистрибутивности:

4. Законы идемпотентности:

5. Законы нуля и единицы:

6. Законы де Моргана:

7. Законы поглощения:

8. Законы склеивания:

9. Закон двойного отрицания:

Дата добавления: 2018-05-12 ; просмотров: 1040 ; Мы поможем в написании вашей работы!

Источник

Читайте также:  Способы сохранения здоровья населения