Способы описания алгоритмов



Правила оформления схем алгоритмов
Условные обозначения и правила выполнения схем алгоритмов регламентируются требованиями Единой системы программной документации в соответствии с ГОСТ 19.701-90 [6].
Схема алгоритма состоит из символов, краткого пояснительного текста и соединяющих линий (см. Приложение). Символы предназначены для графического обозначения отдельных операций, суть которых выражается текстом внутри символов. Символы должны быть по возможности одного размера и располагаться в схеме равномерно, в любой ориентации, но предпочтительным является их горизонтальное расположение.
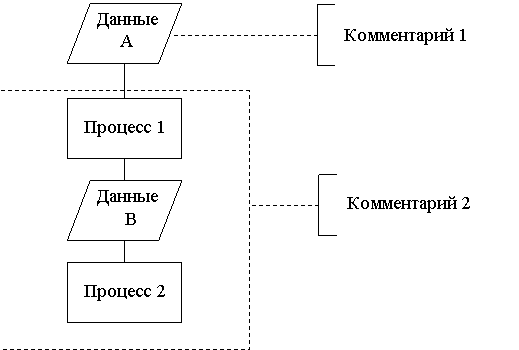
Внутри символа помещается минимальное количество текста, необходимого для понимания функции данного символа. Если такой текст требует значительного увеличения размера символа, то для размещения текста следует использовать символ «комментарий». Пунктирная линия символа «комментарий» связывается с соответствующим символом или может обводить группу символов (рис. 2).
Рис. 2.
Символы в схеме соединяются линиями, которые указывают потоки управления. Направление потока слева направо и сверху вниз считается стандартным. Направление потока, отличное от стандартного, должно быть отмечено стрелкой на конце линии (при вхождении потока в символ или в другую линию потока). Линии должны быть направлены к центру символа. Следует избегать пересечения линий, если потоки в данном месте не входят друг в друга. При необходимости линии в схемах следует разрывать во избежание лишних пересечений или слишком длинных линий, а также, если схема состоит из нескольких страниц. Соединитель в начале разрыва является внешним, а в конце разрыва — внутренним. В комментариях к соединителям могут быть приведены ссылки к страницам (рис.3).
Рис. 3.
Как правило, каждый символ имеет один вход и один выход. Исключение составляют символы:
- «терминатор» (у операции «начало» нет входа, у операции «конец» нет выхода),
- «решение» (один вход и несколько выходов),
- «подготовка» (организация цикла, пример см. на с.33).
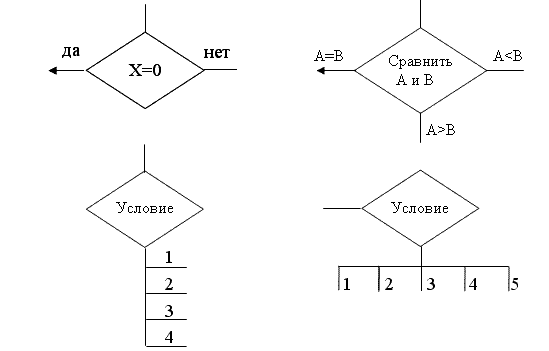
Символ «решение» является логическим. Каждый выход из символа «решение» должен сопровождаться значением условия, приведенного внутри (рис.4).
Рис. 4
Представление алгоритма решения задачи в виде схемы является наиболее наглядным, позволяет проследить процесс прохождения данных, связи между отдельными участками программы. Однако, схема должна быть удобочитаемой, т.е. не должна быть чересчур мелкой, подробной, «перегруженной», чтобы не потерять своей наглядности.
В случае описания решения очень большой, сложной задачи рекомендуется выполнять схему с несколькими уровнями детализации, число которых зависит от размеров и сложности задачи. Уровень детализации должен быть таким, чтобы различные части и взаимосвязь между ними были понятны в целом. При этом весь алгоритм разбивается на смысловые фрагменты, связь между которыми следует указать на более крупной схеме. Сами же фрагменты удобнее выполнять на отдельных страницах, желательно каждый фрагмент размещать на одной странице, не перегружая чрезмерно ссылками и комментариями.
Способы описания алгоритмов
Существуют следующие способы описания (представления) алгоритмов:
1. словесное описание;
2. описание алгоритма с помощью математических формул;
3. графическое описание алгоритма в виде блок-схемы;
4. описание алгоритма с помощью псевдокода;
5. комбинированный способ изображения алгоритма с использованием словесного, графического и др. способов.
Словесное описание алгоритма представляет собой описание структуры алгоритма на естественном языке. Например, к приборам бытовой техники, как правило, прилагается инструкция по эксплуатации, т.е. словесное описание алгоритма, в соответствии с которым данный прибор должен использоваться.
Графическое описание алгоритма в виде блок-схемы – это описание структуры алгоритма с помощью геометрических фигур с линиями связи.
Блок схема алгоритма – это графическое представление метода решения задачи, в котором используются специальные символы для отображения операций.

Символы, из которых состоит блок-схема алгоритма, определяет ГОСТ 19.701-90. Этот ГОСТ соответствует международному стандарту оформления алгоритмов, поэтому блок-схемы алгоритмов, оформленные согласно ГОСТ 19.701-90, в разных странах понимаются однозначно.
Псевдокод – описание структуры алгоритма на естественном, но частично формализованном языке. В псевдокоде используются некоторые формальные конструкции и общепринятая математическая символика. Строгих синтаксических правил для записи псевдокода не предусмотрено.
Рассмотрим простейший пример. Пусть необходимо описать алгоритм вывода на экран монитора наибольшего значения из двух чисел.
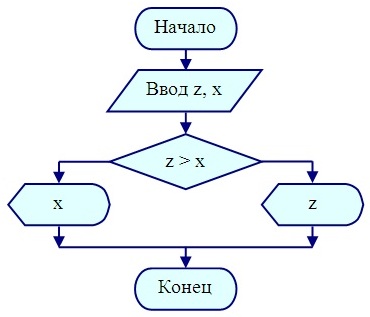
Рисунок 1 — Пример описания алгоритма в виде блок-схемы
Описание этого же алгоритма на псевдокоде:
2. Ввод чисел: Z, X
3. Если Z > X то Вывод Z
4. Иначе вывод Х
Каждый из перечисленных способов изображения алгоритмов имеет и достоинства и недостатки. Например, словесный способ отличается многословностью и отсутствием наглядности, но дает возможность лучше описать отдельные операции. Графический способ более наглядный, но часто возникает необходимость описать некоторые операции в словесной форме. Поэтому при разработке сложных алгоритмов лучше использовать комбинированный способ.
Источник
Способы описания алгоритмов
Существуют несколько способов описания алгоритма: словесное, псевдокод, блок-схема, программа.
Словесное описание представляет структуру алгоритма на естественном языке. Запись алгоритма осуществляется в произвольной форме, никаких правил не существует.
Псевдокод – описание структуры алгоритма на естественном, частично формализованном языке, позволяющее выявить основные этапы решения задачи, перед точной его записью на языке программирования. В псевдокоде используются некоторые формальные конструкции и общепринятая математическая символика.
Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором используемых слов и конструкций.
Блок-схема – описание структуры алгоритма с помощью геометрических фигур с линиями – связями, показывающими порядок выполнения отдельных инструкций. В блок – схеме каждой формальной конструкции соответствует определенная геометрическая фигура или связанная линиями совокупность фигур.
Основные конструкции, использующиеся для построения блок – схем.
 |
 |
 |
— процесс, предназначенный для описания отдельных

 |
 |
ввод/вывод с неопределенного носителя
 |


 |
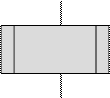 |
— — предопределенный процесс, предназначенный для
— обращения к подпрограмме.
Лекция 5.2. Блок-схемы алгоритма
Алгоритмы решения задач
Логическая структура алгоритма решения любой задачи может быть выражена комбинацией трех базовых структур: следования, ветвления и цикла (это содержание теоремы Бема – Якопини).
Линейная структура (следование) самая важная из структур. Она означает, что действия могут быть выполнены друг за другом (рис. 5.2.1.).
| Выполнить B |
| Выполнить А |
 |  |  |
Прямоугольники могут представлять как одну единственную команду, так и множество операторов, необходимых для выполнения сложной обработки данных.

2. 
3. Вычисляем сумму S = a + b
4. 
 |
| S= a + b |
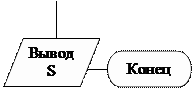 |
Рис. 5.2.2. Блок — схема к примеру 5.2.1.
Ветвление (развилка) – это структура, обеспечивающая выбор между двумя альтернативами. Выполняется проверка условия, а затем выбирается один из путей (рис. 5.2.3). Если условие имеет значение «Истина», то выполняется «Действие А». Если условие имеет значение «Ложь», выполняется «Действие В». Эта структура называется, также «Если – ТО – ИНАЧЕ» или «развилка». Каждый путь (ТО или ИНАЧЕ) ведет к общей точке слияния, так что выполнение алгоритма продолжается независимо от того, какой путь был выбран. Может оказаться, что для одного из результатов проверки ничего выполнять не надо. В этом случае можно применить только один обрабатывающий блок (рис. 5.2.4).

 |
Ложь (НЕТ) Истина (ДА)
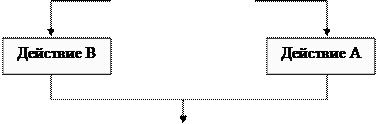 |
Рис. 5.2.3. Полное ветвление
 |


| Действие А |
Рис. 5.2.4. Структура «непол-



Такая структура называется «неполным ветвлением» или «неполной развилкой».
Вывести значение наибольшего числа из двух чисел (рис. 5.2.5).

1. Ввод двух чисел a, b
2. 
ИНАЧЕ «выводим b»
3. 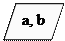









Рис. 5.2.5. Блок – схема к примеру 5.2.2.
 |
Цикл (или повторение) предусматривает повторное выполнение некоторого набора команд алгоритма. Циклы позволяют записать длинные последовательности операций обработки данных с помощью небольшого числа повторяющихся команд. Различают два типа циклов: «цикл с предусловием» и «цикл с постусловием».
Цикл с предусловием («Пока») (рис. 5.2.6).
| Тело цикла |
 | |
 |  |


Рис. 5.2.6. Структура цикла «Пока».
Цикл начинается с проверки логического выражения. Если оно истинно, то выполняется тело цикла, затем все повторяется, пока логическое выражение сохраняет значение «истина». Как только оно становится ложным, выполнение операций прекращается и управление передается дальше. Особенностью цикла с предусловием является то, что если изначально логическое выражение имеет значение «ложь», то тело цикла не выполнится ни разу.
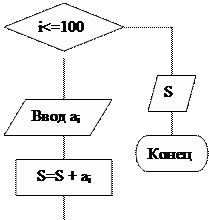
Вычислить сумму 100 чисел (рис. 5.2.7).
8. 



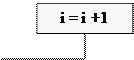 |
Рис. 5.2.7. Блок – схема к примеру 5.2.3 с циклом «Пока»
Цикл с постусловием («До»).




| Тело цикла |



Рис. 5.2.8. Структура «цикла с постусловием».
Вывести максимальное значение из 100 натуральных чисел (рис. 5.2.9).
2. 


| Max=a1; i=2 |
| max = ai |



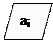




b. ЕСЛИ maxai ТО max = ai
7. 
 |





 |

 |
Рис. 5.2.9. Блок – схема к примеру 5.2.4. с циклом «До»
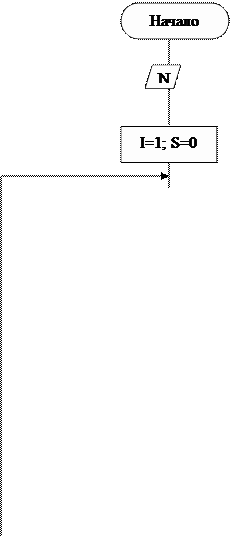
Базовые алгоритмические структуры можно комбинировать одну с другой – как путем организации их следования, так и путем создания суперпозиций (вложений одной структуры в другую). Используя описанные структуры, можно полностью исключить использование каких-либо еще операторов условного и безусловного перехода, что является важным признаком структурного программирования. Приведем несколько примеров (рис. 5.2.10, 5.2.11, 5.2.12, 5.2.13).
 |
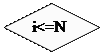
 |
 |
 |
 |
 |
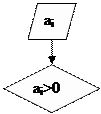
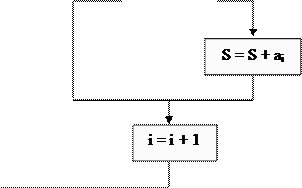
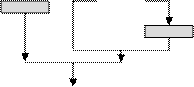
Рис. 5.2.10. Алгоритм типа «развилка, вложенная в цикл, с предусловием», для нахождения суммы положительных чисел и N возможных
 |

 |  |

 |
 |
 |
 |
Рис. 5.2.11. Алгоритм типа «цикл, с предусловием, вложенный в неполную развилку»






— + ную развилку».
 |
Вопросы для самоконтроля
1. Дайте определение алгоритма и поясните его.
2. Какие формы представления алгоритма вы знаете?
3. В чем особенности графического представления алгоритма?
4. Назовите основные (базовые) алгоритмические структуры?
5. Перечислите свойства алгоритмов и объясните, чем они определены.
Статьи к прочтению:
Алгоритм
Похожие статьи:
1. Словесный. Такое описание алгоритма состоит из словесного перечня действий в виде предложений. Например, вычислить C= А-В, если А=В A + B , если A…
Для записи алгоритмов используют различные способы в зависимости от предназначения алгоритма. Рассмотрим следующие способы описания алгоритма:…
Источник