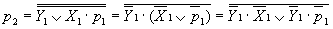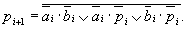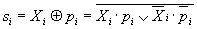Повышение быстродействия сумматоров
Для повышения быстродействия сумматоров можно использовать:
1. параллельное суммирование с последовательным переносом
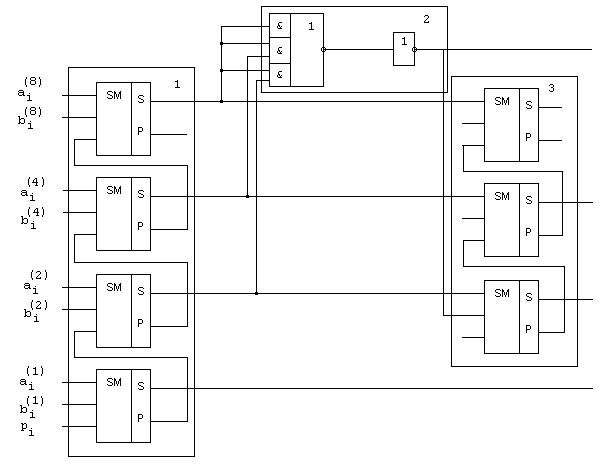
2. параллельное суммирование с параллельным переносом, для этого используется блоки ускоренного переноса (БУП). В них сигнал сложения и сигнал переноса формируется одновременно, схема усложняется, но скорость существенно увеличивается. Схема с использованием БУП выглядит следующим образом:
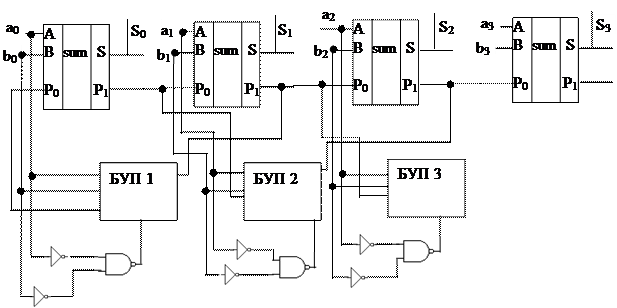 |
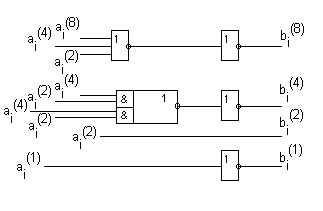
То есть идет одновременное формирование сигнала суммы и оно сразу учитывается при последующем суммировании. Рассмотрим БУП для четырехразрядного сумматора:
Недостатком этой схемы – усложнение схемы в геометрической прогрессии при увеличении разрядности. Реализуется для сложения не более чем четырех разрядов.
3. Для большого количества разрядов используется схема с групповой структурой. Суть метода в том, что одноразрядные сумматоры разбиваются на группы, где n – число разрядов в числе, l – число групп, m – число сумматоров в группе, то есть n=l*m. При этом в каждой группе и между группами могут быть различные виды переноса, то есть можно разбить на четырехразрядные группы и организовать в них БУП.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Многоразрядные параллельные сумматоры
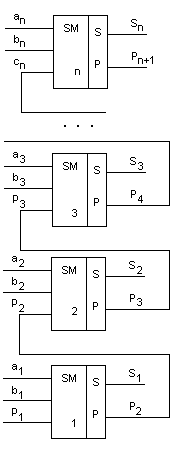
Параллельные многоразрядные сумматоры строятся на основе ПОС. На рис. 15.8 приведена схема параллельного n-разрядного сумматора с последовательным переносом, составленного из одноразрядных сумматоров. Правильные значения
частичных сумм S0 … Sn-1 будут устанавливаться последовательно, начиная с младшего разряда. Самым последним устанавливается правильное значение частичной суммы Sn-1. Максимальное время суммирования в таком сумматоре составляет:
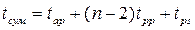
Примером интегрального параллельного сумматора с последовательным переносом является микросхема К564ИМ1. Это — четырёхразрядный сумматор, выполненный по КМДП-технологии. Его структурная схема и УГО показаны соответственно на рис.15.9,а и 15.9,б. Он отличается от схемы рис.15.8 наличием схемы ускоренного формирования выходного переноса c4 (подробно такая схема рассмотрена в п.15.1.4), подаваемого на вход переноса следующей микросхемы при наращивании разрядности. Благодаря наличию такой схемы удаётся увеличить быстродействие многоразрядных параллельных сумматоров с последовательным переносом. При напряжении источника питания Uп =10 В время задержки по трактам от входа c0 до выхода переноса c4 и от входов слагаемых младших разрядов до выхода суммы старшего разряда составляет 140 нc. При Uп = 5 В задержка сигналов увеличивается до 300 нc.
|
|
|
a) б)
|
Недостатком параллельных многоразрядных сумматоров с последовательным переносом является их сравнительно низкое быстродействие, связанное с большим временем суммирования. Увеличение быстродействия сумматоров можно осуществить по двум направлениям :
1) уменьшением параметров tas, tap, tps, tpp и объема оборудования, оцениваемого числом входов используемых ЛЭ;
2) уменьшением времени суммирования tсум .
Первое направление представляет собой классическую задачу синтеза сумматора, не решенную окончательно до настоящего времени. За время существования ЭВМ эта задача решалась эмпирически и были получены удачные решения. В настоящее время широкое распространение получили сумматоры, построенные на основании уравнений (15.5) и (15.8), представляющих самодвойственные функции.
Второе направление связано с уменьшением ( или даже исключением ) влияния разрядности суммируемых чисел на tcyм путем одновременного формирования переносов во все разряды. Такие сумматоры называют параллельными с параллельным переносом. Для синтеза таких сумматоров представим выражение (15.5) для переноса в старший разряд в виде:

или
где 
Сигнал gi = 1 вырабатывается тогда, когда a i = b i =1 и не зависит от значения переноса c i в данный разряд. Поэтому функцию gi = a i b i называют функцией генерации переноса. Сигнал pi = a i 
Для четырехразрядного сумматора функции генерации и распространения переноса будут иметь вид:

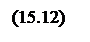



Тогда функции переноса для первого и последующего разрядов можно записать в виде:
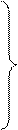

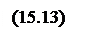
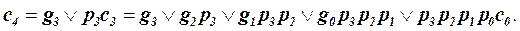 |
Формулы (15.13) показывают, что переносы из каждого разряда можно выразить непосредственно через функции генерации gi и распространения переноса pi, определяемые только значениями слагаемых независимо от их положения в разрядной сетке, и перенос c0 в младший разряд.
Можно показать также, что 
Следовательно, одновременно (параллельно) с формированием сигналов переноса по сформированным значениям функций gi и pi можно формировать частичные суммы si (но небольшая задержка должна быть, чтобы успели выработаться сигналы переноса).
Структурная схема рассмотренного сумматора с параллельным поразрядным переносом приведена на рис. 15.10. Блок генерации и распространения совместно с блоком переноса образуют схему (блок) ускоренного переноса (сокращенно СУП или БУП).
Для реализации этого сумматора в базисе И-НЕ необходимо преобразовать уравнения (15.12) следующим образом:

|

В уравнениях (15.14). (15.17) множители, стоящие после знака 
 |
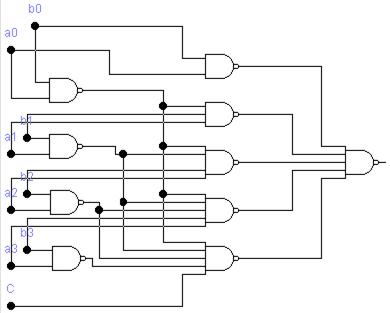
Схема четырехразрядного параллельного сумматора, построенная в соответствии с уравнениями (15.14) . (15.17), приведена на рис.15.11. На этом рисунке пунктирными линиями обведены участки, которые не используются при c0 = 0. Из рисунка видно, что быстродействие параллельного сумматора с параллельным переносом равно времени задержки трех схем И-НЕ, формирующих сигнал переноса, плюс время задержки ПОС. В зависимости от типа одноразрядного сумматора время суммирования при параллельном переносе составляет tсум = (5-6) tзд.ла..
С ростом разрядности сумматора увеличивается число входов конъ-юнкторов, используемых для формирования переносов в старшие разряды. Поэтому сумматоры с параллельным переносом реализуют лишь для малого числа разрядов (обычно для четырех). Однако принцип параллельного переноса используется в широко распространенных сумматорах с групповой структурой.
Источник
Повышение быстродействия параллельных сумматоров.
Для обеспечения высокого быстродействия параллельные сумматоры должны строиться на элементах, обладающих высоким быстродействием.
Трудности в достижении высокого быстродействия сумматора, построенного по схеме на рис. 9.64, связаны с тем, что процесс распространения переносов в нем имеет последовательный характер. Импульс переноса в каждом разряде формируется после того, как будет сформирован и передан импульс переноса из предыдущего разряда. В наиболее неблагоприятном случае возникший в младшем разряде перенос может последовательно вызывать переносы во всех остальных разрядах. При этом время передачи переносов 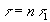
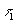
Уменьшение 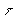
1. При построении схем одноразрядных сумматоров стремятся к уменьшению числа элементов в цепи между входом, на который поступает импульс переноса 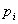
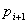
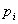
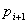
2. В цепях от 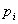
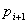
3. Схемы сумматоров следует строить таким образом, чтобы сигналы с выхода каждого логического элемента в цепи от pi к pi+i поступали на возможно меньшее число других логических элементов, так как присоединение каждого дополнительного элемента к той или иной точке цепи переносов, как правило, приводит к увеличению паразитной емкости, удлинению фронтов сигналов и, следовательно, к увеличению задержки распространения сигнала и снижению быстродействия сумматора.
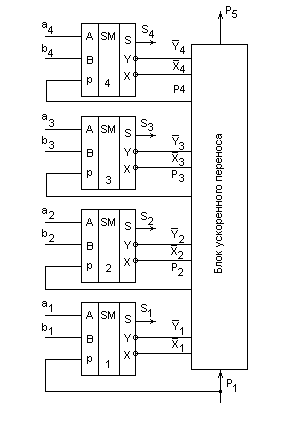
4. Применяют устройства формирования переносов в параллельной форме. В показанном на рис. 9.65 сумматоре с помощью устройства, называемого блоком ускоренного переноса, производится формирование переносов в параллельной форме, т. е. одновременно для всех разрядов. Переносы из этого блока поступают во все разрядные сумматоры одновременно. При этом разрядные сумматоры не содержат цепей формирования переносов, они формируют только сумму s, и величины 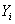
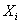
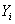
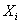
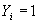
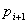
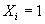
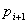
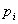
Рассмотрим принцип построения блока ускоренного переноса. Перенос 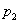
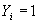
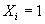
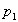
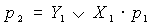
Аналогичные выражения можно построить для переносов в другие разряды:
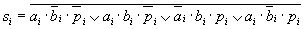
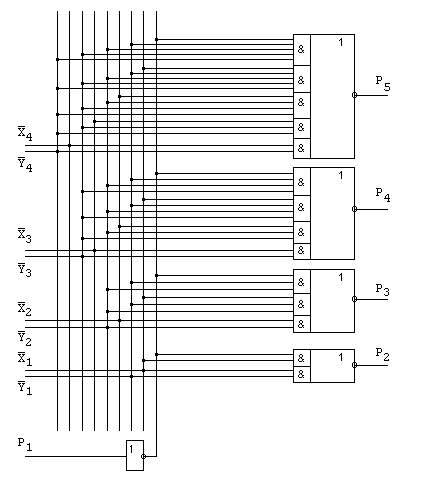
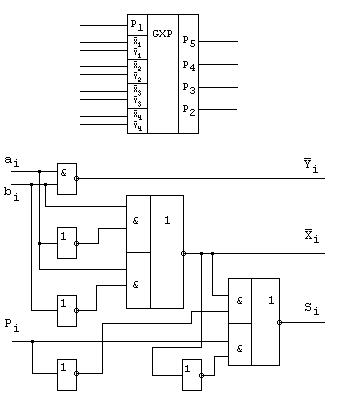
На рис. 9.66,а и б показаны схема блока ускоренного переноса и его условное обозначение.
Входящие в выражения 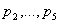
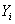
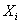
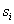
Формирование инверсных значений 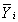
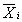
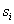
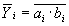
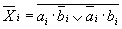
Схема разрядного сумматора, построенного в соответствии с этими выражениями, показана на рис. 9.66,в.
Десятичные сумматоры
Для построения многоразрядных двоичных сумматоров, как было показано выше, необходимы одноразрядные двоичные сумматоры строятся с использованием одноразрядных десятичных сумматоров. Последние выполняют операцию суммирования .десятичных цифр 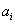
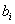
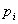
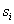
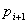

При использовании десятичной системы счисления цифры разрядов десятичного числа представляются в некоторой двоичной форме (см. § 3.2). В связи с этим одна из особенностей одноразрядных десятичных сумматоров связана с тем, что суммируемые Десятичные цифры 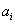
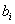
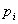
Сумматор для кода 8421.
В работе сумматора этого типа имеются особенности в формировании переноса и суммы, отличающие его от работы двоичного сумматора.
Правила сложения в десятичной системе счисления с использованием кода 8421 рассмотрены в § 3.3. Построенная в соответствии с этими правилами схема одноразрядного десятичного сумматора (рис. 9.67) включает в себя четырехразрядный двоичный сумматор(1), схему формирования переноса 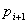
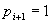
Операция суммирования в случае, когда слагаемые (одно либо оба) имеют отрицательные значения, может производиться с представлением таких слагаемых в обратном коде.
Схема формирования обратного кода.
В десятичной системе счисления обратный код образуется путем преобразования каждой цифры числа в дополнение до 9. В табл. 9.35 приведены для десятичных цифр 0, 1,…, 9 прямые коды и соответствующие им обратные.
Из сопоставления приведенных в таблице значений 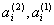
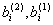
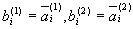
| Таблица 9.35 | |||||||
| Десятичная ячейка | Прямой код 8421 | Обратный код | |||||
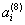 | 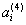 | 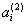 | 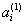 | 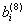 | 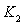 | 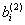 | 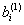 |
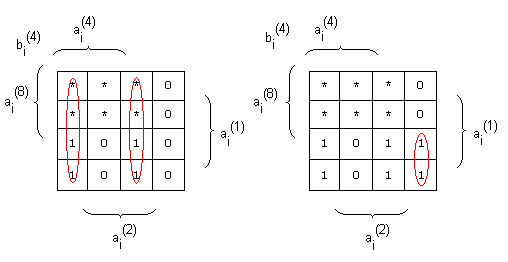
Логические выражения для 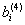
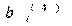
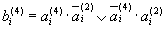
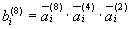
На рис. 3,68 приведена схема, формирующая обратный код по полученным выше логическим выражениям,
| Таблица 9.36 |
 |
АЦП и ЦАП
2.2.6. Принцип аналого-цифрового преобразования информации.
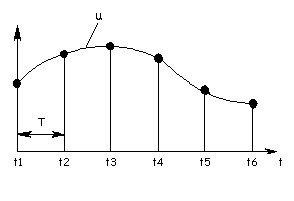
В большинстве случаев получаемый непосредственно от источника информации сигнал оказывается представленным в форме непрерывно меняющегося по своему значению напряжения либо тока (рис. 10.69). Таков, в частности, характер электрического сигнала, соответствующего телефонным, телевизионным и другим видам сообщения. Для передачи таких сообщений по линии связи или для их обработки (например, при отфильтровании помех) могут быть использованы две формы: аналоговая или цифровая. Аналоговая форма предусматривает оперирование со всеми значениями сигнала, цифровая форма с отдельными его значениями, представленными в форме кодовых комбинаций.
Преобразование сигналов из аналоговой формы в цифровую выполняется в устройстве, называемом аналого-цифровым преобразователем (АЦП).
В преобразователе сигналов из аналоговой формы в цифровую можно выделить следующие процессы: дискретизацию, квантование, кодирование. Рассмотрим сущность этих процессов. При этом для определенности в последующем изложении будем считать, что преобразование в цифровую форму осуществляется над сигналом, представленным в форме меняющегося во времени напряжения.
Дискретизация непрерывных сигналов.
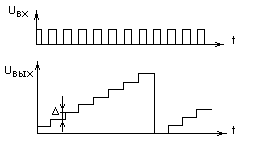
Процесс дискретизации заключается в том, что из непрерывного во времени сигнала выбираются отдельные его значения, соответствующие моментам времени, следующим через определенный временной интервал Т (на рис. 10.69 моменты 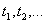
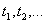
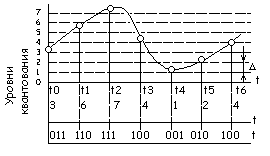
Дискретные значения сигнала следует отсчитывать с таким малым тактовым интервалом Т, чтобы по ним можно было бы восстановить сигнал в аналоговой форме с требуемой точностью.14.1.2. Квантование и кодирование. Сущность этих операций заключается в следующем. Создается сетка так называемых уровней квантования (рис. 10.70), сдвинутых друг относительно друга на •величину Д, называемую шагом квантования. Каждому уровню квантования можно приписать порядковый номер (0, 1, 2, 3 и т.д.). Далее, полученные в результате дискретизации значения исходного аналогового напряжения заменяются ближайшими к ним уровнями квантования. Так, на диаграмме рис. 10.70 значение напряжения в момент 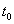
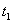
Описанный процесс носит название операции квантования, смысл которого состоит в округлении значений аналогового напряжения, выбранных в тактовые моменты времени. Как и всякое округление, процесс квантования приводит к погрешности (к ошибкам квантования) в представлении дискретных значений напряжения, создавая так называемый шум квантования. При проектировании АЦП стремятся снизить шум квантования до такого уровня, при котором он еще обеспечивает требуемую точность представления сигнала. Подробнее шум квантования будет рассмотрен далее.
Следующая операция, выполняемая при аналого-цифровом преобразовании сигналов, — кодирование. Смысл ее состоит в следующем. Округление значения напряжения, осуществляемое при операции квантования, позволяет эти значения представлять числами — номерами соответствующих уровней квантования. Для диаграммы, представленной на рис. 10.70, образуется последовательность чисел: 3, 6, 7, 4, 1, 2 и т.д. Далее, получаемая таким образом последовательность чисел представляется двоичным кодом.
Вернемся к искажениям, связанным с процессом квантования, названным шумом квантования. При телефонной связи шум квантования воспринимается ухом человека действительно в виде шума, сопровождающего речь.
Так как в процессе квантования значение напряжения в каждый тактовый момент времени округляется до ближайшего уровня квантования, ошибка в представлении значений напряжения оказывается в пределах 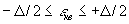
Следовательно, чем больше шаг квантования 
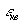
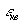
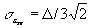
Уменьшение шума квантования достигается только уменьшением шага квантования 


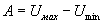
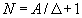
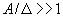
Отсюда видно, что уменьшение шума квантования путем уменьшения 
При организации телефонной связи номера уровней квантования обычно выражают семи-восьмиразрядными двоичными числами, а число уровней квантования оказывается равным 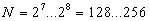
Наряду с рассмотренными выше погрешностями — погрешностями квантования — при аналого-цифровом преобразовании возникают погрешности аппаратурные, связанные с неточностью работы отдельных узлов АЦП. Эти погрешности будут выявляться далее при рассмотрении различных схемных построений АЦП.
Источник