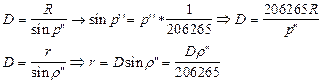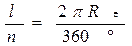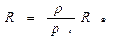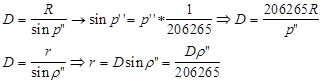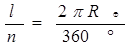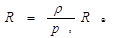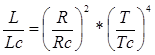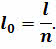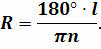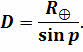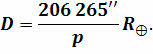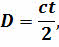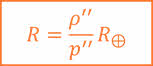Перечислите известные вам способы определения расстояний до тел солнечной системы

БИЛЕТ № 6. Способы определения расстояний до тел Солнечной системы и их размеров

1. Способы определения расстояний до тел Солнечной системы и их размеров.

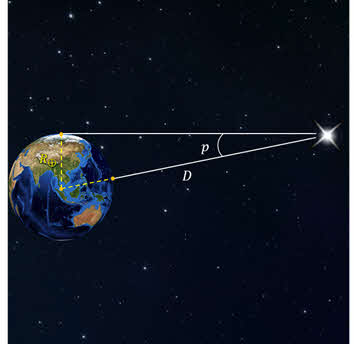
Сперва определяется расстояние до какой-нибудь доступной точки. Это расстояние называется базисом. Угол, под которым из недоступного места виден базис, называют параллаксом. Горизонтальным параллаксом называют угол, под которым с планеты виден радиус Земли, перпендикулярный лучу зрения.

p² – параллакс, r² – угловой радиус, R – радиус Земли, r – радиус светила.

Радиолокационный метод.Он заключается в том, что на небесное тело посылают мощный кратковременный им­пульс, а затем принимают отраженный сигнал. Скорость распространения радиоволн равна скорости света в вакууме: известна. Поэтому если точно измерить время, которое потребовалось сигналу, чтобы дойти до небесного тела и возвратиться обратно, то легко вычислить искомое расстояние.

Радиолокационные наблюдения позволяют с большой точностью определять расстояния до небесных тел Солнечной системы. Этим методом уточнены расстояния до Луны, Венеры, Меркурия, Марса, Юпитера.

Лазерная локация Луны.Вскоре после изобретения мощных источников светового излучения — оптических квантовых генераторов (лазеров) — стали проводиться опыты по лазерной локации Луны. Метод лазерной локации анало­гичен радиолокации, однако точность измерения значи­тельно выше. Оптическая локация дает возможность опреде­лить расстояние между выбранными точками лунной и зем­ной поверхности с точностью до сантиметров.

Для определения размеров Земли определяют расстояние между двумя пунктами, расположенными на одном меридиане, затем длину дуги l, соответствующей 1° —n.

Для определения размеров тел Солнечной системы можно измерить угол, под которым они видны земному наблюдателю – угловой радиус светила r и расстояние до светила D.

Учитывая p₀ – горизонтальный параллакс светила и, что углы p_{0 и} r малы,

1. Определение светимости звезды на основе данных о ее размерах и температуре.

Источник

Какие есть способы определения расстояний до тел Солнечной системы?

Способы определения расстояний до тел Солнечной системы и их размеров.

Сперва определяется расстояние до какой-нибудь доступной точки. Это расстояние называется базисом. Угол, под которым из недоступного места виден базис, называют параллаксом. Горизонтальным параллаксом называют угол, под которым с планеты виден радиус Земли, перпендикулярный лучу зрения.
p² – параллакс, r² – угловой радиус, R – радиус Земли, r – радиус светила.

Радиолокационный метод. Он заключается в том, что на небесное тело посылают мощный кратковременный им­пульс, а затем принимают отраженный сигнал. Скорость распространения радиоволн равна скорости света в вакууме: известна. Поэтому если точно измерить время, которое потребовалось сигналу, чтобы дойти до небесного тела и возвратиться обратно, то легко вычислить искомое расстояние.

Радиолокационные наблюдения позволяют с большой точностью определять расстояния до небесных тел Солнечной системы. Этим методом уточнены расстояния до Луны, Венеры, Меркурия, Марса, Юпитера.

Лазерная локация Луны. Вскоре после изобретения мощных источников светового излучения — оптических квантовых генераторов (лазеров) — стали проводиться опыты по лазерной локации Луны. Метод лазерной локации анало­гичен радиолокации, однако точность измерения значи­тельно выше. Оптическая локация дает возможность опреде­лить расстояние между выбранными точками лунной и зем­ной поверхности с точностью до сантиметров.
Подробнее:

Источник

TechStandard

Способы определения расстояний до тел Солнечной системы и их размеров.

Сперва определяется расстояние до какой-нибудь доступной точки. Это расстояние называется базисом. Угол, под которым из недоступного места виден базис, называют параллаксом

. Горизонтальным параллаксом называют угол, под которым с планеты виден радиус Земли, перпендикулярный лучу зрения.

p² – параллакс, r² – угловой радиус, R – радиус Земли, r – радиус светила.

Он заключается в том, что на небесное тело посылают мощный кратковременный им­пульс, а затем принимают отраженный сигнал. Скорость распространения радиоволн равна скорости света в вакууме: известна. Поэтому если точно измерить время, которое потребовалось сигналу, чтобы дойти до небесного тела и возвратиться обратно, то легко вычислить искомое расстояние.

Радиолокационные наблюдения позволяют с большой точностью определять расстояния до небесных тел Солнечной системы. Этим методом уточнены расстояния до Луны, Венеры, Меркурия, Марса, Юпитера.

Лазерная локация Луны.

Вскоре после изобретения мощных источников светового излучения — оптических квантовых генераторов (лазеров) — стали проводиться опыты по лазерной локации Луны. Метод лазерной локации анало­гичен радиолокации, однако точность измерения значи­тельно выше. Оптическая локация дает возможность опреде­лить расстояние между выбранными точками лунной и зем­ной поверхности с точностью до сантиметров.

Для определения размеров Земли определяют расстояние между двумя пунктами, расположенными на одном меридиане, затем длину дуги l, соответствующей 1° -n.

Для определения размеров тел Солнечной системы можно измерить угол, под которым они видны земному наблюдателю – угловой радиус светила r и расстояние до светила D.

Учитывая p0 – горизонтальный параллакс светила и, что углы p0 и r малы,

1. Определение светимости звезды на основе данных о ее размерах и температуре.

L – светимость (Lc = 1)

R – радиус (Rc = 1)

T – Температура (Tc = 6000)

Дополнительно

Есть ли жизнь на Марсе
«Есть ли жизнь на Марсе, нет ли жизни на Марсе — науке неизвестно» — это не просто удачный афоризм из популярной кинокомедии «Карнавальная ночь», который широко вошел в наш разговорный язык и стал ходячей шуткой. Главное здесь в том, что эта фраза очень долгое время отражала наш действитель .

Внутренняя структура протона и новый способ получения энергии
Протон был открыт в начале 20-х г.г. в экспериментах с альфа-частицами. В опытах по рассеянию на протонах электронов и гамма-квантов были получены достоверные доказательства существования некой внутренней структуры у этой частицы. В 1970 г. в Стенфордском центре линейного ускорителя (СЛАК) удалось .

Источник

Презентация по астрономии на тему: «Определение расстояний до тел Солнечной системы и размеров небесных тел»

Описание презентации по отдельным слайдам:

Определение расстояний до тел Солнечной системы и размеров этих тел Учитель физики ВКК МБОУ СОШ № 54 г. Воронежа Кутузова Ирина Валериевна

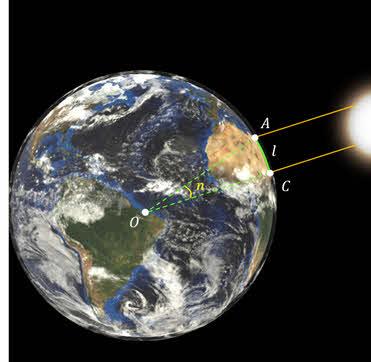
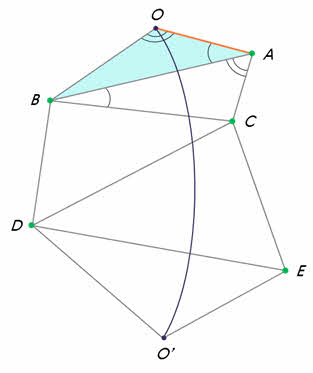
1. Геометрический метод (по параллаксам) В – точка, в которой находится наблюдатель; А – доступная точка; С – недоступная точка АВ – базис (измеряется непосредственно) Углы измеряются геодезическим инструментом

1. Геометрический метод (по параллаксам) Угол α, под которым из недоступного места виден базис, называется параллаксом

1. Геометрический метод (по параллаксам) В пределах Солнечной системы в качестве базиса используют экваториальный радиус Земли

1. Геометрический метод (по параллаксам) Угол р0 , под которым со светила, находящегося на горизонте, был бы виден экваториальный радиус Земли, называется горизонтальным экваториальным параллаксом светила

1. Геометрический метод (по параллаксам) Если горизонтальный параллакс найден, то расстояние до светила вычисляется по формуле: где D – расстояние от центра Земли до центра какого либо тела Солнечной системы; ‒ экваториальный радиус Земли

1. Геометрический метод (по параллаксам) Поскольку углы р0 очень малы, то их синусы можно заменить самими углами, если величина угла выражена в радианах: но обычно р0 выражено в секундах дуги, поэтому:

1. Геометрический метод (по параллаксам) Тогда: Параллакс выражен в секундах дуги, а D – либо в километрах, либо в радиусах Земли

2. Радиолокационный метод Радиолокация заключается в том, что на небесное тело посылают мощный кратковременный радиоимпульс, а потом принимают отраженный сигнал

2. Радиолокационный метод Зная скорость света в вакууме: с = 299 792 458 м/с и точно измерив время прохождения сигнала туда и обратно, легко вычислить расстояние до небесного тела

2. Радиолокационный метод Радиолокационные наблюдения позволяют с большой точностью определять расстояния до небесных тел Солнечной системы. Этим методом уточнены расстояния до Луны, Венеры, Меркурия, Марса, Юпитера

3. Лазерная локация Метод аналогичен радиолокации, однако точность гораздо выше. Лазерная локация позволяет определять расстояния между точками лунной и земной поверхности с точностью до сантиметров

4. Определение размеров тел Солнечной системы При наблюдениях небесных тел Солнечной системы можно измерить угол ρ, под которым они видны земному наблюдателю

4. Определение размеров тел Солнечной системы Зная этот угловой радиус светила ρ и расстояние до светила D, можно вычислить линейный радиус R:

4. Определение размеров тел Солнечной системы Учитывая ранее полученную формулу для D, получим:

4. Определение размеров тел Солнечной системы А так как углы малы, то:

Во сколько раз линейный радиус Солнца превышает радиус Земли, если угловой радиус Солнца 16´? Дано: Решение

Спасибо за внимание!

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-165564

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

В проекте КоАП отказались от штрафов для школ

Время чтения: 2 минуты

В 16 регионах ввели обязательную вакцинацию для студентов старше 18 лет

Время чтения: 1 минута

Шойгу предложил включить географию в число вступительных экзаменов в вузы

Время чтения: 1 минута

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Определение расстояний и размеров тел в Солнечной системе

Урок 14. Астрономия 11 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Определение расстояний и размеров тел в Солнечной системе»

Вы уже знаете, что ещё в Древней Греции учёными и мыслителями было установлено, что наша планета не является плоской, а имеет шарообразную форму. Представление о Земле как о шаре, который свободно, без всякой опоры находится в космическом пространстве, является одним из величайших достижений древнего мира.

Первый известный науке метод определения размеров Земли применил греческий учёный Эратосфен, живший в Египте. Его идея была достаточно проста. Итак, Эратосфен выбрал два города — Александрию и Сиену (ныне Асуан) — расположенных на одном земном меридиане.

Далее он обозначил длину дуги меридиана между двумя городами через l, а её угловое значение в градусах как п.

Тогда длина дуги в 1 о выбранного меридиана равна

С другой стороны, он знал, что длина окружности равна: L = 2πR.

Приравняв правые части последних двух уравнений, легко получить искомый радиус земного шара:

Теперь было необходимо определить длину дуги меридиана в градусной мере. Очевидно, что она равна разности географических широт Александрии и Сиены. Так вот, чтобы определить эту разность Эратосфен придумал хитрый способ. Он знал, что в полдень дня летнего Солнцестояния в Сиене Солнце находится в зените и освещает дно самых глубоких колодцев. А в Александрии Солнце до зенита не доходит. Поэтому шест, вбитый вертикально в землю должен отбрасывать тень. Измерив длину этой тени можно легко определить искомую длину дуги меридиана, которая у Эратосфена оказалась равной 7,2 о .

Ну а расстояние между Александрией и Сиеной ему было хорошо известно: оно составляло пять тысяч греческих стадий.

Подставив все данные в формулу для длины окружности меридиана, Эратосфен получил значение в 250 000 стадий.

Стадий — это весьма неоднозначная единица измерения расстояния. Но, как правило, за стадий принимали расстояние, которое проходит легковооружённый воин за промежуток времени от появления первого луча солнца при его восходе до того момента, когда весь солнечный диск окажется над горизонтом.

Однако если учесть, что расстояние между Александрией и Асуаном по прямой примерно равно 844 километрам, то можно полагать, что одна стадия примерно равна 169 метрам.

Тогда искомая длина всей окружности меридиана равна 42 250 километрам, что совсем не плохо для того времени.

Современная наука располагает более точными способами измерения расстояний на земной поверхности. Одним из них является метод триангуляций, основанный на явлении параллактического смещения.

Параллактическое смещение — это изменение направления на предмет при перемещении наблюдателя. С его помощью можно измерить расстояние на основе измерения длины одной из сторон (базиса) и двух прилегающих к ней углов в треугольнике.

Суть метода триангуляций состоит в следующем. По обе стороны дуги, длину которой нужно измерить, выбирается несколько точек на расстоянии не более 50 километров друг от друга, на которых устанавливаются геодезические вышки. При этом из каждой точки должны быть видны по крайней мере две другие точки. Далее тщательным образом измеряется длина базиса (с точностью до одного миллиметра). После этого с вершины вышки при помощи теодолита измеряются углы между направлениями на два-три соседних пункта. Измерив углы в треугольнике, одной из сторон которого является базис, геодезисты получают возможность вычислить длину двух других его сторон по известным тригонометрическим формулам. Проводя затем измерение углов из пунктов, расстояние между которыми уже вычислено, можно узнать длину очередных двух сторон и так далее. Затем, по вычисленным сторонам, определяется искомая длина дуги.

В XVIII веке использование триангуляционных измерений в экваториальных широтах и вблизи северного полярного круга, показало, что длина дуги в 1 о меридиана не одинакова и увеличивается к полюсам. Из этого следовало, что наша планета не является идеальным шаром и её полярный радиус почти на 21 километр короче экваториального. Поэтому в геодезии и форму Земли считают геоидом, то есть телом с поверхностью, близкой к поверхности спокойного океана и продолженной под материками.

В настоящее время форму Земли принято характеризовать следующими физическими характеристиками:

· полярное сжатие — 0,0033528;

· экваториальный радиус — 6378,1 км;

· полярный радиус — 6356,8 км;

· средний радиус — 6371,0 км;

· и длина окружности экватора — 40 075,017 км.

Долгое время загадкой для многих астрономов являлось истинное расстояние от Земли до Солнца. Измерить его смогли лишь во второй половине XVIII века, когда был впервые определён горизонтальный параллакс Солнца. По сути дела, при этом измеряется параллактическое смещение объекта, находящегося за пределами Земли, а базисом является её радиус.

Горизонтальным параллаксом называется угол, под которым со светила виден радиус Земли, перпендикулярный лучу зрения.

Зная горизонтальный параллакс светила, можно, по известным тригонометрическим соотношениям, определить его расстояние от центра Земли:

Очевидно, что чем дальше расположено светило, те меньше его горизонтальный параллакс. Например, наибольший параллакс, в среднем 57ʹ, имеет спутник Земли — Луна. У Солнца он значительно меньше и примерно составляет 8,794ʹʹ. Такому параллаксу соответствует среднее расстояние от Земли до Солнца, примерно равное 149,6 миллиона километров.

На одном из прошлых уроков мы говорили о том, что это расстояние в астрономии принимается за одну астрономическую единицу. С её помощью удобно измерять расстояния между телами в Солнечной системе.

Но вернёмся к нашей формуле. Итак, из геометрии вам должно быть известно, что при малых значениях угла его синус примерно равен самому углу, выраженному в радианах. Если учесть, что в одном радиане содержится 206 265ʹʹ, то легко можно получить формулу, удобную для вычислений:

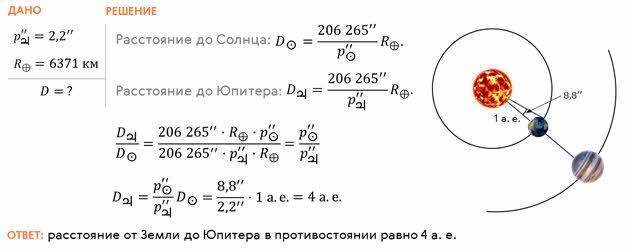
Для примера, давайте с вами определим расстояние от Земли до Юпитера в момент противостояния, если его горизонтальный параллакс был равен 2,2ʹʹ. Радиус Земли примем равным 6371 километру.

Эту же задачу можно было решить несколько иначе.

В настоящее время для более точного определения расстояний до тел в Солнечной системе применяется более точный метод измерений — радиолокационный. Измерив время, необходимое для того, чтобы радиолокационный импульс достиг небесного тела, отразился и вернулся на Землю, вычисляют расстояние до этого тела по формуле:

где с — это скорость света в вакууме.

С разработкой методов определения расстояний до тел в Солнечной системе учёным не составило большого труда придумать и способ определения их размеров. В частности, при наблюдениях небесного тела Солнечной системы с Земли можно измерить угол, под которым оно видно наблюдателю, то есть его угловой размер (или угловой диаметр), а, следовательно, и угловой радиус.

А зная угловой радиус и расстояние до светила, можно вычислить его линейный радиус:

.

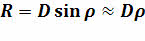
Только в этой формуле угловой радиус должен быть выражен в радианах.

Если в записанное уравнение подставить формулу для определения расстояний методом горизонтального параллакса и упростить её, используя тот факт, что значения углов ρ и р малы, то получим формулу, по которой можно определять линейные размеры небесных тел:

Но помните, пользоваться ей можно тогда, когда видны диски светил.

Для примера давайте решим с вами такую задачу. При наблюдении прохождения Меркурия по диску Солнца определили, что его угловой радиус равен 5,5’’, а горизонтальный параллакс — 14,4’’. Чему равен линейный радиус Меркурия?

Источник