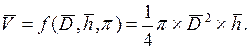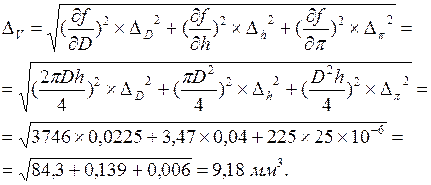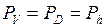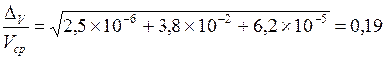Относительная погрешность косвенным способом

Относительная погрешность косвенным способом

Погрешности прямых измерений. Промах. Систематическая погрешность. Случайная погрешность. Полная погрешность. Погрешности косвенных измерений. Запись результата измерений

1. Оценка погрешности прямых измерений

Измерить физическую величину – это значит сравнить ее с однородной величиной, принятой за единицу меры.

Различают прямые и косвенные измерения.

Если измеряемая величина непосредственно сравнивается с мерой, то измерения называются прямыми. Например, измерения линейных размеров тел с помощью масштабной линейки и т.д.

Если измеряется не сама искомая величина, а некоторые другие величины, связанные с ней функциональной зависимостью, то измерения называются косвенными. Например, измерения объема, ускорения и т.д.

Из-за несовершенства средств и методик измерения, органов чувств при любом измерении неизбежны отклонения результатов измерений от истинных величин. Эти отклонения называются погрешностями измерений.

Погрешности измерений делятся на систематические, случайные и промахи.

1.1. Промахи, связанные с неправильными отсчетами по прибору, неправильными записями и т.д., приводят к очень большой по абсолютной величине погрешности. Они, как правило, не укладываются в общую закономерность измеренных величин. Обнаруженный промах следует отбросить.

1.2. Систематическими погрешностями Δx_сист называются погрешности, которые сохраняются при повторных измерениях одной и той же величины x или изменяются по определенному закону.

Систематические погрешности подразделяются на несколько групп. Отметим только приборную погрешность.

Систематическая приборная погрешность определяется по классу точности прибора, который указывается на приборе следующими цифрами: 0,01; 0,02; 0,05; 1,0; 2,5; 4,0. Класс точности показывает предельно допустимое значение систематической погрешности, выраженной в процентах от верхнего предела на выбранном диапазоне измерений. Например, предел измерения вольтметра с классом точности 0,5 равен 200 В. Систематическая погрешность равна 0,5% от 200В. Следовательно, систематическая погрешность вольтметра равна 1 В.

Если на приборе класс точности не указан, то погрешность равна половине цены наименьшего деления шкалы прибора.

1.3. Случайными называются погрешности, которые изменяются беспорядочно при повторных измерениях одной и той же физической величины при одинаковых условиях.

Оценим случайную погрешность. Пусть при измерении какой-либо физической величины было произведено N измерений и были получены значения x₁, x₂, … x_N. Тогда наиболее вероятным значением измеряемой величины является ее среднее арифметическое значение

Результаты измерений x₁, x₂, … x_N «рассеиваются» вокруг среднего. В качестве меры «рассеяния» результатов наблюдения вокруг среднего служит среднее квадратичное отклонение

Пусть a будет истинным, но неизвестным значением измеряемой величины x. Доказано, что вероятность попадания результатов измерения величины x в интервал значений от (a – S) до (a + S) оказывается равной α = 0,68.

Вероятность попадания результатов наблюдений в более широкие интервалы (a – 2S, a + 2S) и (a – 3S, a + 3S) равна α = 0,95 и α = 0,99 соответственно.

Вероятность попадания в заданный интервал значений величины x называется доверительной вероятностью, а сам интервал – доверительным интервалом.

Однако, таким образом полученный доверительный интервал справедлив при большом значении N. В учебных лабораториях, как правило, приходится ограничиваться небольшим числом измерений. В этом случае доверительный интервал находят с помощью коэффициента Стьюдента, который зависит от числа измерений N и доверительной вероятности α. В таблице 1 приведены коэффициенты Стьюдента для различного числа наблюдений при доверительных вероятностях α = 0,68; 0,95; 0,99.

Источник

Относительная погрешность косвенным способом

В лабораторной практике большинство измерений – косвенные и интересующая нас величина является функцией одной или нескольких непосредственно измеряемых величин:

Как следует из теории вероятностей, среднее значение величины определяется подстановкой в формулу (13) средних значений непосредственно измеряемых величин, т.е.

Требуется найти абсолютную и относительную ошибки этой функции, если известны ошибки независимых переменных.

Рассмотрим два крайних случая, когда ошибки являются либо систематическими, либо случайными. Единого мнения относительно вычисления систематической ошибки косвенных измерений нет. Однако, если исходить из определения систематической ошибки как максимально возможной ошибки, то целесообразно находить систематическую ошибку по формулам

частные производные функции N = ƒ(x, y, z, . ) по аргументу x, y, z. найденные в предположении, что все остальные аргументы, кроме того, по которому находится производная, постоянные;
δx, δy, δz – систематические ошибки аргументов.

Формулой (15) удобно пользоваться в случае, если функция имеет вид суммы или разности аргументов. Выражение (16) применять целесообразно, если функция имеет вид произведения или частного аргументов.

Для нахождения случайной ошибки косвенных измерений следует пользоваться формулами:

где Δx, Δy, Δz, . – доверительные интервалы при заданных доверительных вероятностях (надежностях) для аргументов x, y, z, . . Следует иметь в виду, что доверительные интервалы Δx, Δy, Δz, . должны быть взяты при одинаковой доверительной вероятности P₁ = P₂ = . = P_n = P.

В этом случае надежность для доверительного интервала ΔN будет тоже P.

Формулой (17) удобно пользоваться в случае, если функция N = ƒ(x, y, z, . ) имеет вид суммы или разности аргументов. Формулой (18) удобно пользоваться в случае, если функция N = ƒ(x, y, z, . ) имеет вид произведения или частного аргументов.

Часто наблюдается случай, когда систематическая ошибка и случайная ошибка близки друг к другу, и они обе в одинаковой степени определяют точность результата. В этом случае общая ошибка ∑ находится как квадратичная сумма случайной Δ и систематической δ ошибок с вероятностью не менее чем P, где P – доверительная вероятность случайной ошибки:

При проведении косвенных измерений в невоспроизводимых условиях функцию находят для каждого отдельного измерения, а доверительный интервал вычисляют для получения значений искомой величины по тому же методу, что и для прямых измерений.

Следует отметить, что в случае функциональной зависимости, выраженной формулой, удобной для логарифмирования, проще сначала определить относительную погрешность, а затем из выражения ΔN = ε ¯ N найти абсолютную погрешность.

Прежде чем приступать к измерениям, всегда нужно подумать о последующих расчетах и выписать формулы, по которым будут рассчитываться погрешности. Эти формулы позволят понять, какие измерения следует производить особенно тщательно, а на какие не нужно тратить больших усилий.

При обработке результатов косвенных измерений предлагается следующий порядок операций:

1. Все величины, находимые прямыми измерениями, обработайте в соответствии с правилами обработки результатов прямых измерений. При этом для всех измеряемых величин задайте одно и то же значение надежности P.
2. Оцените точность результата косвенных измерений по формулам (15) – (16), где производные вычислите при средних значениях величин.
   Если ошибка отдельных измерений входит в результат дифференцирования несколько раз, то надо сгруппировать все члены, содержащие одинаковый дифференциал, и выражения в скобках, стоящие перед дифференциалом взять по модулю; знак d заменить на Δ (или δ).
3. Если случайная и систематическая ошибки по величине близки друг к другу, то сложите их по правилу сложения ошибок. Если одна из ошибок меньше другой в три или более раз, то меньшую отбросьте.
4. Результат измерения запишите в виде:

Приведем примеры расчета ошибки косвенного измерения.

Пример 1.Находится объем цилиндра по формуле

где d – диаметр цилиндра, h – высота цилиндра.

Обе эти величины определяются непосредственно. Пусть измерение этих величин дало следующие результаты:

h = (8.65 ± 0.02) мм, при одинаковой надежности Р = 0.95.

Среднее значение объема, согласно (14) равно

Воспользовавшись выражением (18) имеем:

Так как измерения производились микрометром, цена деления которого 0.01 мм , систематические ошибки
δd = δh = 0.01 мм. На основании (16) систематическая ошибка δV будет

Систематическая ошибка оказывается сравнимой со случайной, следовательно

Таким образом, результат измерения оказывается

Пример 2. Найти абсолютную и относительную погрешности для следующей функциональной зависимости:

В этом случае удобнее сначала искать относительную погрешность. Тогда

До сих пор подразумевается математический смысл дифференциала, и знаки слагаемых учитываются. Раскроем теперь выражение d(m₁ + m₂ — m₃) = dm₁ + dm₂ — dm₃ и разделим почленно на знаменатель. Затем объединим все члены, содержащие дифференциалы одной и той же переменной:

Используя формулу (18), получим

Абсолютную случайную погрешность найдем из выражения

Используя формулу (16) получаем

Абсолютную систематическую ошибку найдем из выражения

Приведем таблицу расчета систематических погрешностей для простейших функций.

N	ƒ	δƒ	ε =δƒ/ƒ	N	ƒ	δƒ	ε =δƒ/ƒ
1	x + y	δx + δy	(δx + δy)/(x + y)	6	x 1/n	δx / (n · x (n-1)/n )	δx/(nx)
2	x — y	δx + δy	(δx + δy)/(x — y)	7	sin x	cos x· δx	δx/tg x
3	x · y	xδy + yδx	(δx/x) + (δy/y)	8	cos x	sin x· δx	tg x· δx
4	x/y	(xδy + yδx)/y 2	(δx/x) + (δy/y)	9	tg x	δx/cos 2 x	2δx/sin 2x
5	x n	nx n-1 · δx	nδx/x	10	ln x	δx/x	δx/(x · ln x)

Таблица расчета случайных погрешностей для простейших функций.

Источник

Погрешности косвенных измерений

Теперь необходимо рассмотреть вопрос о том, как находить погрешность физической величины U, которая определяется путем косвенных измерений. Общий вид уравнения измерения

где Х_j – различные физические величины, которые получены экспериментатором путем прямых измерений, или физические константы, известные с заданной точностью. В формуле они являются аргументами функции.

В практике измерений широко используют два способа расчета погрешности косвенных измерений. Оба способа дают практически одинаковый результат.

Способ 1.Сначала находится абсолютная D, а затем относительная d погрешности. Этот способ рекомендуется для таких уравнений измерения, которые содержат суммы и разности аргументов.

Общая формула для расчета абсолютной погрешности при косвенных измерениях физической величины Y для произвольного вида f функции имеет вид:

(1.5)

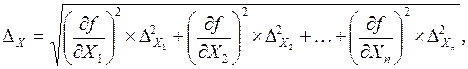
где частные производные функции Y=f(Х₁, Х₂, … , Х_n) по аргументу Х_j,

общая погрешность прямых измерений величины Х_j.

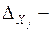
Для нахождения относительной погрешности нужно прежде всего найти среднее значение величины Y. Для этого в уравнение измерения (1.4) надо подставить средние арифметические значения величин X_j.

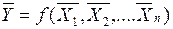
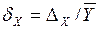
То есть среднее значение величины Y равно: . Теперь легко найти относительную погрешность: .

Пример: найти погрешность измерения объёма V цилиндра. Высоту h и диаметр D цилиндра считаем определёнными путём прямых измерений, причём пусть количество измерений n=10.

Формула для расчета объёма цилиндра, то есть уравнение измерения имеет вид:

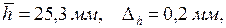
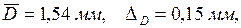
Пусть при Р=0,68;

при Р=0,68.

Тогда, подставляя в формулу (1.5) средние значения, найдём:

Погрешность D_V в данном примере зависит, как видно, в основном от погрешности измерения диаметра.

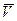
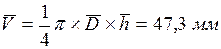
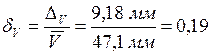
Средний объём равен: , относительная погрешность d_V равна:

, или d_V=19%.

Окончательный результат после округления:

Способ 2. Этот способ определения погрешности косвенных измерений отличается от первого способа меньшими математическими трудностями, поэтому его чаще используют.

В начале находят относительную погрешность d, и только затем абсолютную D. Особенно удобен этот способ, если уравнение измерения содержит только произведения и отношения аргументов.

Порядок действий можно рассмотреть на том же конкретном примере — определение погрешности при измерении объёма цилиндра

.

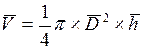
Все численные значения входящих в формулу величин сохраним теми же, что и при расчетах по способу 1.

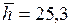
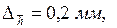
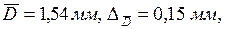
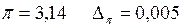
Пусть мм, ; при Р=0,68;

; при Р=0,68.

-погрешность округления числа p (см. рис. 1.1)

При использовании способа 2 следует действовать так:

1) прологарифмировать уравнение измерения (берём натуральный логарифм)

.

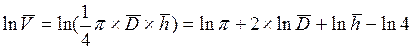
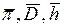
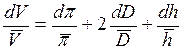
найти дифференциалы от левой и правой частей, считая независимыми переменными,

;

2) заменить дифференциал каждой величины на абсолютную погрешность этой же величины, а знаки “минус”, если же они есть перед погрешностями на “плюс”:

;

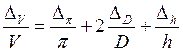
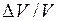
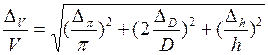
3) казалось бы, что с помощью этой формулы уже можно дать оценку для относительной погрешности , однако это не так. Требуется так оценить погрешность, чтобы доверительная вероятность этой оценки совпадала с доверительными вероятностями оценки погрешностей тех членов, которые стоят в правой части формулы. Для этого, чтобы это условие выполнялось, нужно все члены последней формулы возвести в квадрат, а затем извлечь корень квадратный из обеих частей уравнения:

.

Или в других обозначениях относительная погрешность объёма равна:

,

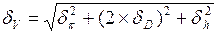
причём вероятность этой оценки погрешности объёма будет совпадать с вероятностью оценки погрешностей входящих в подкоренное выражение членов:

Сделав вычисления, убедимся, что результат совпадает с оценкой по способу 1:

Теперь, зная относительную погрешность, находим абсолютную:

Окончательный результат после округления:

V = (47 ± 9) мм 3 , d_V = 19%, P=0,68.

Контрольные вопросы

1. В чём заключается задача физических измерений?

2. Какие типы измерений различают?

3. Как классифицируют погрешности измерений?

4. Что такое абсолютная и относительная погрешности?

5. Что такое промахи, систематические и случайные погрешности?

6. Как оценить систематическую погрешность?

7. Что такое среднее арифметическое значение измеренной величины?

8. Как оценить величину случайной погрешности, как она связана со средним квадратичным отклонением?

9. Чему равна вероятность обнаружения истинного значение измеренной величины в интервале от Х_ср — s до Х_ср + s?

10. Если в качестве оценки для случайной погрешности выбрать величину 2s или 3s, то с какой вероятностью истинное значение будет попадать в определённые этими оценками интервалы?

11. Как суммировать погрешности и когда это нужно делать?

12. Как округлить абсолютную погрешность и среднее значение результата измерения?

13. Какие способы существуют для оценки погрешностей при косвенных измерениях? Как при этом действовать?

14. Что нужно записать в качестве результата измерения? Какие величины указать?

Дата добавления: 2015-02-19 ; просмотров: 5102 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник