Отделение корней при решении нелинейных уравнений можно выполнить двумя способами

3.1. Отделение корней нелинейного уравнения

Отделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a, b], которому он принадлежит.

На первом этапе определяется число корней, их тип. Определяется интервал, в котором находятся эти корни, или определяются приближенные значения корней.

В инженерных расчетах, как правило, необходимо определять только вещественные корни. Задача отделения вещественных корней решается Аналитическими и Графическими методами.

Аналитические методы основаны на функциональном анализе.

Для алгебраического многочлена n-ой степени (полинома) с действительными коэффициентами вида

Pn(x) = an x n + an-1xn-1 +. +a1x+ a0 = 0, (an >0) (3.2)

Верхняя граница положительных действительных корней определяется по формуле Лагранжа (Маклорена):

, (3.3)

Где: k ³ 1 – номер первого из отрицательных коэффициентов полинома;

B – максимальный по модулю отрицательный коэффициент.

Нижнюю границу положительных действительных корней можно определить из вспомогательного уравнения

(3.4)

Если для этого уравнения по формуле Лагранжа верхняя граница равна R1, то

= (3.5)

Тогда все положительные корни многочлена лежат в интервале

≤x+≤.

Интервал отрицательных действительных корней многочлена определяется с использованием следующих вспомогательных функций.

и .

≤x–≤ = =.

Рассмотрим пример отделения корней с использованием этого аналитического метода.

Методом Лагранжа определим границы положительных и отрицательных корней многочлена.

3×8 – 5×7 – 6×3 – x – 9 = 0

K = 1 B = |– 9| an = 3

= 4

9×8 + x7 + 6×5 + 5x – 3 = 0

k = 8 B = 3 an = 9

Отсюда границы положительных корней 0,5 ≤ x+ ≤ 4

3×8 + 5×7 + 6×3 + x – 9 = 0

=

9×8 – x7 – 6×5 – 5x – 3 = 0

K = 1 B = 6 an = 9

Следовательно, границы отрицательных корней –2 ≤ x– ≤ –0,6

Формула Лагранжа позволяет оценить интервал, в котором находятся все действительные корни, положительные или отрицательные. Поэтому, для определения расположения каждого корня необходимо проводить дополнительные исследования.

Для трансцендентных уравнений не существует общего метода оценки интервала, в котором находятся корни. Для этих уравнений оцениваются значения функции в особых точках: разрыва, экстремума, перегиба и других.

На практике получил большее распространение Графический метод приближённой оценки вещественных корней. Для этих целей строится график функции по вычисленным её значениям.

Графически корни можно отделить 2-мя способами:

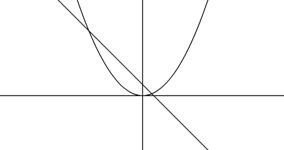
1. Построить график функции y = f(x) и определить координаты пересечений с осью абсцисс− это приближенные значения корней уравнения.На графике 3 корня.

Рис. 3.1 Отделение корней на графике f(x).

2. Преобразовать f(x)=0 к виду j(x) = y(x), где j(x) и y(x) – элементарные функции, и определить абсциссу пересечений графиков этих функций.

На графике 2 корня.

Рис. 3.2 Отделение корней по графикам функций j(x) и y(x).

Графический метод решения нелинейных уравнений широко применяется в технических расчётах, где не требуется высокая точность.

Для отделения вещественных корней можно использовать ЭВМ. Алгоритм отделения корней основан на факте Изменения знака функции в окрестности корня. Действительно, если корень вещественный, то график функции пересекает ось абсцисс, а знак функции изменяется на противоположный.

Рассмотрим Схему алгоритма отделения корней нелинейного уравнения на заданном отрезке в области определения функции.

Алгоритм позволяет определить приближённые значения всех действительных корней на отрезке [a, b]. Введя незначительные изменения в алгоритм, его можно использовать для определения приближённого значения максимального или минимального корня.

Приращение неизвестного Δx не следует выбирать слишком большим, чтобы не «проскочить» два корня.

Недостаток метода – использование большого количества машинного времени.

Источник

Решение нелинейных уравнений

Сайт:	Электронные курсы ТПУ
Курс:	Информационные технологии 1
Книга:	Решение нелинейных уравнений
Напечатано::	Гость
Дата:	Пятница, 19 Ноябрь 2021, 21:53

Оглавление

Решение нелинейных уравнений

При решении нелинейных уравнений невозможно выразить переменную. В этих случаях целесообразно применить ряд численных методов нахождения корней уравнения. Ниже рассмотрены некоторые из них.

Любое уравнение можно представить в виде f (x) = 0 , перенеся всё в одну сторону, тогда поиск корней уравнения сводится к поиску точек пересечения функции f (x) с осью абсцисс. Для более удобной реализации методов в языке Паскаль целесообразно сразу описать функцию f (x) как подпрограмму:

function F(x:real):real;

begin

F:= . ;

end;

Существует ряд методов численного решения нелинейных уравнений, целесообразность применения каждого из которых определяется видом уравнения, его порядком, требуемой точностью и т. д. Эти методы подробно рассмотрены в [1,2,5].

Метод отделения корней

Итак, дано уравнение ƒ(x) = 0, где ƒ(x) – непрерывная функция. Поиск корней уравнения сводится к поиску точек пересечения функции ƒ(x ) с осью абсцисс. Все рассматриваемые ниже методы подразумевают, что уже найден отрезок [a,b], в котором существует один корень уравнения. В зависимости от вида функции таких отрезков может быть несколько, а для периодических функций – бесконечное множество. Метод отделения корней осуществляет поиск таких отрезков.

Наиболее наглядным является графический способ отделения корней. Для реализации этого метода необходимо построить график функции. Это будет легко сделать, если составить программу, которая будет выдавать таблицу значений функции при меняющемся с некоторым шагом h аргументе x (см. рис. 1).

Если есть такая таблица значений функции, то график функции можно и не строить. Достаточно найти две строчки, где значение функции меняет знак на противоположный. Такой способ называется табличным методом отделения корней (см. пример).

Рис. 1. Графическая интерпретация метода отделения корней

Пример. 4.1. Реализация табличного метода отделения корней.

Здесь x пробегает значения от x_n до x_k с шагом h и при этом на экран выводятся значения x и f(x). Отрезок [x_n, x_k] и шаг h нужно подбирать для каждой функции, исходя из её характера. Шаг должен быть меньше, чем расстояние между корнями уравнения, чтобы исключить попадание в шаг двух корней.

program tablica;

var xn,xk,x,h:real;

function F(x:real):real;

begin F:=sqrt(x)+2*sqr(x)+3*x; end;

begin

write(‘Введите начало интервала > ’); readln(xn);

write(‘Введите конец интервала > ’); readln(xk);

write(‘Введите шаг > ’); readln ( h );

x:=xn;

begin

writeln(‘x=’,x,‘ f(x)=’,f(x));

x:=x+h;

end;

end.

Процесс выбора отрезка [a,b], содержащего корень, можно автоматизировать. Для этого нужно, начиная с какого-то начального значения, смещать отрезок длиной h в цикле и каждый раз анализировать значения функции на концах этого отрезка. Корень присутствует, если эти значения разного знака. Можно использовать сложное условие
(f(a)>0 AND f(b) 0),

Читайте также:  Методика обоснования выбора лучшего способа долгосрочного финансирования

а можно просто найти произведение и проверить его знак. Корень присутствует, если f(a)*f(b) . После этого можно уточнять значение корня, а можно перейти к поиску следующего отрезка, задав начало поиска от конца найденного.

Пример. 4.2. Поиск ближайшего отрезка, содержащего корень.

program poisk;

var a,b,h:real;

function F(x:real):real;

begin F:=sqrt(x)+2*sqr(x)+3*x; end;

begin

write(‘Введите начало поиска > ’); readln(b);

write(‘Введите шаг > ’); readln ( h );

repeat

a:=b;

b:=a+h;

until f(a)*f(b)

writeln(‘a=’,a,‘ b=’,b);

end.

Метод половинного деления

Пусть дано уравнение ƒ(x) = 0, где ƒ ( x ) – непрерывная функция, корень Р отделен на отрезке [a,b], т. е. ƒ(a) × ƒ(b) > 0, причем | b – a | ƒ (a) и ƒ (b) одного знака и, следовательно, ƒ (a) × ƒ b) > 0, то вычисляются значения функции в точках, расположенных через равные интервалы на оси Х. Когда ƒ (a_n) и ƒ (b_n) имеют противоположные знаки, то значения a = a_n и b=b_n принимаются в качестве начальных и находят середину отрезка [a,b], т. е. с=(a+b)/2. Тогда отрезок [a,b] точкой с разделится на два равных отрезка [a,c] и [c,b], длина которых равна (b–a)/2. Из двух этих образовавшихся отрезков выбирается тот, на концах которого функция ƒ (x) принимает значения противоположных знаков; обозначим его [a₁,b₁]. Затем отрезок [a₁,b₁] делим пополам и проводим те же действия. Получим отрезок [a₂,b₂], длина которого равна (b–a)/2 2 . Процесс деления отрезка пополам производится до тех пор, когда на каком-то k-м этапе будет получен отрезок [a_k,b_k], такой, что

где число k указывает на количество проведенных делений. Числа a_k и b_k – корни уравнения ƒ (x) = 0 с точностью до E. За приближенное значение корня следует взять Р=(a_k+b_k)/2, причем погрешность не превысит (b–a)/2 k+ 1 .

Рис. 2. Графическая интерпретация метода половинного деления

Отметим, что в качестве условия прекращения счета более целесообразно пользоваться условием E ≤ I b_k – a_k I .

Блок-схема алгоритма представлена на рис. 3.

Рассмотренный метод имеет относительно малую скорость сходимости, но отличается от других методов простотой реализации алгоритма, не требующего вычисления производных заданной функции.

На блок-схеме видно два цикла. Первый реализует поиск отрезка [a,b] длиной h, на котором есть корень уравнения. Второй цикл уменьшает этот отрезок методом половинного деления до тех пор, пока его длина не станет меньше заданной погрешности е. Удобнее всего для организации циклов применить оператор repeat … until. Внутри второго цикла размещён условный оператор, который проверяет, с какой стороны нужно уменьшить отрезок [a,b].

Рис. 3. Блок-схема алгоритма метода половинного деления

Метод касательных

Расчетная формула метода касательных (или метод Ньютона-Рафсона) получается из разложения функции ƒ(x) = 0 в ряд Тейлора в окрестности точки x_n. При ограничении разложения двумя членами ряда получим

Здесь O (от английского order) означает порядок остаточного члена в разложении, который в дальнейшем считается малым.

.

Обычно окончательная формула записывается в виде

.

Таким образом, зная какое-либо предыдущее приближение x_n, где n – номер приближения или итерации (n ≥ 0), можно определить последующее приближенное значение корня x_n+1. Если заданное (x_n) и расчетное (x_n+1) значения совпадают с точностью ε, т. е.

Читайте также:  Толкование права понятие способы виды функции

то значение x_n+1 считается приближенным значением корня уравнения ƒ (x) = 0.

Кроме предыдущего условия окончания счета, можно использовать условие малости функций ƒ (x) около корня, т. е. | ƒ (x_n)| ≤ ε_f или | ƒ (x_n+1) | ≤ ε_f , где ε_f – заданная погрешность.

Рассмотрим геометрическое толкование метода касательных (см. рис. 4), где значение корня Р определяется следующим образом.

» width=»480″ height=»248.97959183673″ alt=» »/>

Рис. 4. Графическая интерпретация метода касательных

Исходя из некоторого начального приближения x_n, находим соответствующее ему значение ƒ (x_n) (точка А), проводим касательную к кривой ƒ (x) через точку А и ищем точку пересечения этой касательной с осью Х. Эта точка будет значением x_n+1, т. к. требовалось провести через точку с координатами x_n, ¦(x_n) прямую с угловым коэффициентом ƒ ‘(x_n) и затем найти её пересечение с осью Х.

Величина отрезка (x_n – x_n+1) больше заданной погрешности e, поэтому поиск значения корня продолжается аналогично. Принимая последнее найденное значение x_n+1 за исходное, определяем следующее значение x_n+2 по той же формуле

» width=»189″ height=»52″ alt=» »/>,

далее опять проверяется условие

Повторение поиска следующей точки продолжается до тех пор, пока не выполнится условие окончания поиска приближенного значения корня.

Для составления программ можно руководствоваться блок-схемой, представленной на рис. 5.

» width=»468″ height=»406″ alt=» »/>

Рис. 4.5. Блок-схема алгоритма метода касательных

Наличие в блок-схеме вывода f(x₁) означает дополнительную проверку правильности определения корня, т. к. в этом случае значение функции должно быть близко к нулю.

Замечание. При реализации этого метода целесообразно функцию ¦(x) и её производную ¦ ‘ (x) описать как подпрограммы:

function F(x:real):real;

begin F:= . ; end;

function F1(x:real):real;

begin F1:= . ; end;

При этом функция должна быть предварительно продифференцирована вручную.

Основной цикл удобнее всего организовать при помощи оператора repeat … until.

Метод касательных обладает относительно большой скоростью сходимости при выполнении следующих условий:

1. Начальное приближение x₀ выбрано достаточно близко к корню уравнения ƒ (x) = 0.
2. Вторая производная ƒ «(x) не принимает больших значений.
3. Первая производная ƒ ‘ (x) не слишком близка к нулю.

Важно помнить, что успешность поиска корня напрямую зависит от того, насколько близко к корню выбрано начальное приближение. Поэтому иногда целесообразно вначале провести поиск отрезка, содержащего корень, методом отделения корней, как это было сделано перед реализацией метода половинного деления. Подбирая необходимый шаг, можно легко найти такой отрезок. Тогда в качестве первого приближения можно взять любой из его концов или середину этого отрезка.

Модифицированный метод Ньютона

Модифицированный метод Ньютона лишь немного отличается от метода касательных и обладает меньшей скоростью сходимости. Здесь значение производной вычисляется всего один раз в точке первого приближения и больше не изменяется. Следовательно, её вычисление будет стоять до оператора цикла. Общая формула вычисления последующего приближения будет выглядеть так:

Источник