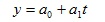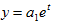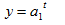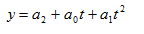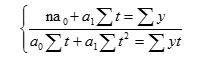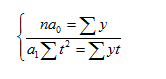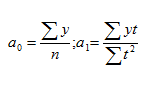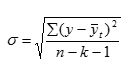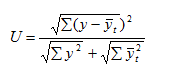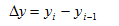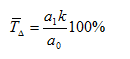Основные способы выравнивания ряда динамики для выделения тренда

Методы выявления основной тенденции (тренда) в рядах динамики

Поможем написать любую работу на аналогичную тему

Одна из основных задач изучения рядов динамики – выявить основную тенденцию (закономерность) в изменении уровней ряда, именуемую трендом. Закономерность в изменении уровней ряда в одних случаях проявляется наглядно, в других – может маскироваться колебаниями случайного или неслучайного характера. Поэтому, чтобы сделать правильные выводы о закономерностях развития того или иного показателя, надо суметь отделить тренд от колебаний, вызванных случайными кратковременными причинами. На основании выделенного тренда можно экстраполировать (прогнозировать) развитие явления в будущем. С этой целью (устранить колебания, вызванные случайными причинами) ряды динамики подвергают обработке.

Существует несколько методов обработки рядов динамики, помогающих выявить основную тенденцию изменения уровней ряда, а именно: метод укрупнения интервалов, метод скользящей средней и аналитическое выравнивание. Во всех методах вместо фактических уровней при обработке ряда рассчитываются иные (расчетные) уровни, в которых тем или иным способом взаимопогашается действие случайных факторов и тем самым уменьшается колеблемость уровней. Последние в результате становятся как бы «выравненными», «сглаженными» по отношению к исходным фактическим данным. Такие методы обработки рядов динамики называются сглаживанием или выравниванием рядов динамики.

Простейший метод сглаживания уровней ряда – укрупнения интервалов, для определяется итоговое значение или средняя величина исследуемого показателя. Этот метод особенно эффективен, если первоначальные уровни ряда относятся к коротким промежуткам времени. Например, если имеются данные о ежесуточном производстве мороженого на предприятии за месяц, то, естественно, в таком ряду возможны значительные колебания уровней, так как чем меньше период, за который приводятся данные, тем больше влияние случайных факторов. Чтобы устранить это влияние, рекомендуется укрупнить интервалы времени, например до 5 или 10 дней, и для этих укрупненных интервалов рассчитать общий или среднесуточный объем производства (соответственно по пятидневкам или декадам). В ряду с укрупненными интервалами времени закономерность изменения уровней будет более наглядной. Или, например, имеются ежемесячные данные о производстве мороженого – табл.32, еще более сильно укрупним интервалы – до трех месяцев (см. табл.33).

По своей сути метод скользящей средней похож на метод укрупнения интервалов, но в данном случае фактические уровни заменяются средними уровнями, рассчитанными для последовательно подвижных (скользящих) укрупненных интервалов, охватывающих m уровней ряда. Например, если принять m=3, то сначала рассчитывается средняя величина из первых трех уровней, затем находится средняя величина из 2-го, 3-го и 4-го уровней, потом из 3-го, 4-го и 5-го и т.д., т.е. каждый раз в сумме трех уровней появляется новый уровень, а два остаются прежними, что и обусловливает взаимопогашение случайных колебаний в средних уровнях. Рассчитанные из m членов скользящие средние относятся к середине (центру) каждого рассматриваемого интервала.

Сглаживание методом скользящей средней можно проводить по любому числу членов m, но удобнее, если m – нечетное число, так как в этом случае скользящая средняя сразу относится к конкретной временнОй точке – середине (центру) интервала. Если же m – четное, то скользящая средняя относится к промежутку между временнЫми точками: например, при сглаживании по четырем членам (m=4) средняя из первых четырех уровней будет находиться между второй и третьей временной точкой, следующая – между третьей и четвертой и т.д. Тогда, чтобы сглаженные уровни относились непосредственно к конкретным временнЫм точкам, из каждой пары смежных промежуточных значений скользящих средних находят среднюю арифметическую, которую относят к временной точке, находящейся между смежными. Такой прием двойного расчета сглаженных уровней называется центрированием.

Недостатком метода скользящей средней является то, что сглаженный ряд укорачивается по сравнению с фактическим с двух концов: при нечетном m на (m-1)/2, а при четном m – на m/2 с каждого конца. Применяя этот метод, надо помнить, что он сглаживает (устраняет) лишь случайные колебания. Если же, например, ряд содержит сезонную волну (см. 6.6), она сохранится и после сглаживания методом скользящей средней. Кроме того, этот метод сглаживания, как и метод укрупнения интервалов не позволяет выражать общую тенденцию изменения уровней в виде математической модели.

Наиболее совершенным методом обработки рядов динамики в целях устранения случайных колебаний и выявления тренда является выравнивание уровней ряда по аналитическим формулам (или аналитическое выравнивание). Суть аналитического выравнивания заключается в замене эмпирических (фактических, исходных) уровней yi теоретическими , которые рассчитаны по определенному уравнению, принятому за математическую модель тренда, где теоретические уровни рассматриваются как функция времени: = f(t).

При этом каждый фактический уровень yi рассматривается обычно как сумма двух составляющих:

, (90)

где f(t) =­ ­- систематическая составляющая, отражающая тренд и выраженная определенным уравнением; — случайная величина, вызывающая колебания уровней вокруг тренда.

Задача аналитического выравнивания сводится к следующему:

1) определение на основе фактических данных формы (вида) гипотетической функции = f(t), способной наиболее адекватно отразить тенденцию развития исследуемого показателя;

2) нахождение по эмпирическим данным параметров указанной функции (уравнения);

3) расчет по найденному уравнению теоретических (выравненных) уровней.

В аналитическом выравнивании наиболее часто используются простейшие функции, представленные в табл. 30, где обозначено — теоретические (выравненные) уровни (читается как «игрек, выравненный по t»); t – условное обозначение времени (1, 2, 3 …); a0, a1, a2, . – параметры аналитической функции; k – число гармоник (при выравнивании по ряду Фурье).

Выбор той или иной функции для выравнивания ряда динамики осуществляется на основании графического изображения эмпирических данных. Если по тем или иным причинам уровни эмпирического ряда трудно описать одной функцией, следует разбить анализируемый период на отдельные части и затем выровнять каждую часть по соответствующей кривой.

Таблица 30. Виды математических функций[30], используемые при выравнивании

Источник

Способы выявления и выделения тренда

Проверка ряда на наличие в нём тренда возможна способами: 1. Графический метод; 2. Метод средних -ряд динамики делится на 2 части и для них находятся средние, если они различаются более чем на 10%, то признаётся наличие тренда.3.Метод Кокса и Стюарта-ряд делится на 3 равные части, находятся средние и сравниваются 1 и 3 части, если они различаются более чем на 10%, то признаётся наличие тренда.4.Метод Валлиса и Мура- наличие тренда признаётся, если ряд не содержит либо содержит в приемлемом количестве фаз. Непосредственное выделение тренда: 1.Укрупнение интервалов — ряд динамики делят на достаточно большое число равных интервалов, если интервальные средние не позволяют увидеть тенденцию, то увеличивают размах интервала, количество интервалов уменьшается. 2.Метод скользящей средней- уровни ряда заменяются средними значениями, получаемыми из данного уровня и нескольких симметрично окружающих его уровней- интервалы сглаживания. Недостатком данного метода является то, что значения уровня начала и конца ряда условны.3.Метод аналитического выравнивания- формализация основной проявляющейся во времени тенденции развития изучаемого явления. Для аналитического выравнивания используется линейная функция .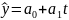

Методы выравнивания рядов динамики

В ходе обработки динамического ряда важнейшей задачей является выявление основной тенденции развития явления (тренда) и сглаживание случайных колебаний. Для решения этой задачи в статистике существуют особые способы, которые называют методами выравнивания. Выделяют три основных способа обработки динамического ряда: а) укрупнение интервалов динамического ряда и расчет средних для каждого укрупненного интервала; б) метод скользящей средней; в) аналитическое выравнивание (выравнивание по аналитическим формулам). Укрупнение интервалов — наиболее простой способ. Он заключается в преобразовании первоначальных рядов динамики в более крупные по продолжительности временных периодов, что позволяет более четко выявить действие основной тенденции (основных факторов) изменения уровней. По интервальным рядам итоги исчисляются путем простого суммирования уровней первоначальных рядов. Для других случаев расcчитывают средние величины укрупненных рядов (переменная средняя). Переменная средняя рассчитывается по формулам простой средней арифметической. Скользящая средняя — это такая динамическая средняя, которая последовательно рассчитывается при передвижении на один интервал при заданной продолжительности периода. Первую рассчитанную центрированную относят ко второму периоду, вторую — к третьему, третью — к четвертому и т.д. По сравнению с фактическим сглаженный ряд становится короче. Важнейшим способом количественного

выражения общей тенденции изменения уровней динамического ряда является аналитическое выравнивание ряда динамики, которое позволяет получить описание плавной линии развития ряда. При этом эмпирические уровни заменяются уровнями, которые рассчитываются на основе определенной кривой, где уравнение рассматривается как функция времени. Вид уравнения зависит от конкретного характера динамики развития. Его можно определить как теоретически, так и практически. Теоретический анализ основывается на рассчитанных показателях динамики. Практический анализ — на исследовании линейной диаграммы. Задачей аналитического выравнивания является определение не только общей тенденции развития явления, но и некоторых недостающих значений как внутри периода, так и за его пределами.

Источник

Динамические ряды — краткое руководство по анализу изменений явлений во времени

Даная статья понятными и простыми терминами объяснит, что же такое динамические ряды, для чего они нужны, как производится анализ полученных данных и какие возможности открываются перед теми, кто владеет методикой данного анализа. Любое явление в области здравоохранения нуждается в тщательной оценке, и здесь знания анализа динамических рядов неоценимы. С помощью динамического ряда можно оценить и спрогнозировать проблематику любой нозологической единицы, сформировать дальнейшую тактику лечения и меры профилактики заболеваний.

Динамический ряд — ряд однородных величин, характеризующих изменение явления во времени.

Целью анализа динамических рядов является:

• выявление закономерности изменения изучаемого явления во времени;
• прогнозирование (экстраполирование) полученных данных на последующие
  годы.

Числовые значения, составляющие динамический ряд, называются уровнями ряда (у).

Типы динамических рядов:

1. В зависимости от вида уровня ряда:

а) простые (уровень ряда выражен абсолютными числами);

б) сложные (уровень ряда выражен обобщающими коэффициентами).

1. В зависимости от способа формирования временного интервала:

а) моментные (данные собираются на определенный момент времени);

б) интервальные (данные собираются за определенный период времени).

1. В зависимости от выраженности изменений явления во времени (определя­ется по коэффициенту корреляции между временем и изучаемым явлением).

а) с выраженной тенденцией (r =0,7 — 1,0);

б) с неустойчивой тенденцией (r =0,3 — 0,69);

в) с отсутствием тенденции ( r = 0 — 0,29).

Основное требование, предъявляемое к анализируемым динамическим ря­дам, заключается в сопоставимости их уровней. Для оценки сопоставимости прово­дят предварительный анализ полученных данных по следующим критериям:

• единство территории, на которой проводился сбор данных;
• единая методология учета данных;
• единые временные интервалы, в течение которых проводилась регистрация
  данных.

Методика анализа динамических рядов

Методика аналитики предусматривает выполнение последовательных действий:

1. Представить полученные данные графически и выявить форму зависимости изучаемого явления от времени.
2. Оценить наличие и силу корреляции изучаемого явления от времени.
3. Если установлено, что ряд обладает выраженной тенденцией, проводят анализ компонентов динамики ряда: основной тенденции (эволюции, тренда), кратковременных систематических движений и случайных колебаний. Основная задача анализа — разделить эти компоненты и выявить основную закономерность изменения явления во времени. Для выявления и описания тренда динамический ряд подвергают обработке — выравниванию.

Способы выравнивания динамических рядов

Чтобы произвести выравнивание динамических рядов потребуются следующие действия:

• Укрупнение временных интервалов (периодов), в течение которых изучается явление.
• Сглаживание ряда методом скользящей средней.
• Аналитический способ.

При этом способе на основании фактических данных подбирается наиболее подходящее для отражения тенденции развития явления математическое уравнение (аппроксимирующая функция), которое принимается за модель развития явления во времени. Т.е. уровни ряда рассматриваются как функция времени, и задача выравнивания сводится к определению вида функции, отысканию ее параметров по эмпирическим данным и расчету по найденной формуле теоретических выравненных уровней. Наиболее часто используются следующие функции:

а) линейная зависимость:

б) экспоненциальная зависимость:

в) показательная зависимость:

г) параболическая зависимость:

у – теоретический уровень;

t – временной интервал.

В качестве примера возьмем линейную зависимость и проведем выравнивание, используя для нахождения параметров уравнения а₀ ,а₁ способ наименьших квадратов. Способ наименьших квадратов позволяет найти теоретическую кривую, максимально приближенную к эмпирической, а условие минимума суммы квадратов отклонений теоретических данных от фактических позволяет свести математическое решение задачи к системе нормальных уравнений:

где у — уровни фактического ряда;

n — количество уровней;

t — порядковый номер временного периода.

Эта система уравнений легко упрощается, если «t» присвоить ранги (порядковые номера), ведя отсчет времени от середины ряда. При нечетном ряде середина обозначается через 0, а отсчет рангов ведется через единицу с соответствующим знаком в ту или иную сторону от середины (например: -5,-4,-3,-2,-1, 0,+1.+2,+3,->:4,+5). При четном ряде две средние временные точки обозначаются через +1 и -1, а остальные ранги присваиваются через две единицы (например: -5,-3,-1,+1,+3,+5).

При отсчете времени от середины ряда St = 0 и система нормальных уравнений принимает вид:

Отсюда находим параметры уравнения:

Подставляя в уравнение у = а₀ + а₁t вместо «t» его ранги, находим выравненные (теоретические) значения уровней ряда и строим теоретическую кривую выравненного динамического ряда.

При использовании аналитического способа всегда отмечается отклонение теоретических уровней от фактических уровней ряда, которое может быть обуслов­лено как случайными колебаниями, так и неправильно подобранным аппроксими­рующим уравнением. В связи с этим заключительным этапом выравнивания динамического ряда аналитическим способом является оценка точности аппроксимации с определенным уровнем значимости.

Оценка точности аппроксимации возможна с помощью нахождения

Для получения точной оценки необходимо найти такие величины:

а) коэффициент вариации:

где у- фактический уровень ряда;

y_t — теоретический уровень ряда;

k- число параметров уравнения;

n- число уровней ряда.

Аппроксимация считается точной при C_v не более 15%.

б) коэффициент расхождения Тейла:

где у — фактический уровень ряда;

y_t — теоретический уровень ряда.

Аппроксимация считается точной при U не более 5%

После аналитического выравнивания динамического ряда и описания тренда возможно экстраполировать полученные данные. Экстраполяция — предположение о сохранении тренда, базирующееся на допущении неизменности влияющих факто­ров и предшествующей тенденции. Осуществляется путем подставления в найденное уравнение аппроксимации не фактического значения временного интервала, а предполагаемого порядкового номера (ранг) того периода, на который прогнозируется результат.

Вычисление основных показателей динамического ряда

Алгоритм вычислений ведущих параметров динамических рядов:

yi- текущий уровень (сравниваемый);

у_i-1— базисный уровень (с каким сравнивают);

t- период времени, в течение которого уровень предполагается неизменным.

1.Абсолютный прирост (убыль) :

2.Темп роста (убыли):

3.Темп прироста (относительная скорость), темп убыли :

4.Средний темп прироста (убыли):

где а₀; а₁ — параметры уравнения;

k = 1 при нечетном ряде;

k = 2 при четном ряде.

5.1% прироста (убыли): используются при сравнении динамических рядов с уровнями, выраженными различными обобщающими коэффициентами.

Таким образом, с помощью данного руководства по определению и расчетам такого понятия, как, динамические ряды, специалисты различных отраслей медицины, ученые могут эффективно и быстро оценить изменение различных величин в течение времени.

Благодарим за интерес, проявленный к нашей статье, оставайтесь с нами!

Источник