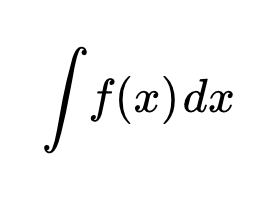Основные способы вычисления интегралов

Методы вычисления неопределенных интегралов

Первообразная и неопределенный интеграл

Первообразная F(x) от функции f(x) – это такая функция, производная которой равна f(x) :
F′(x) = f(x), x ∈ Δ ,
где Δ – промежуток, на котором выполняется данное уравнение.

Совокупность всех первообразных называется неопределенным интегралом:
,
где C – постоянная, не зависящая от переменной x .

Основные формулы и методы интегрирования

Таблица интегралов

Конечная цель вычисления неопределенных интегралов — путем преобразований, привести заданный интеграл к выражению, содержащему простейшие или табличные интегралы.
См. Таблица интегралов >>>

Правило интегрирования суммы (разности)

.
Здесь и далее u, v, w – функции от переменной x .

Вынесение постоянной за знак интеграла

Пусть c – постоянная, не зависящая от x . Тогда ее можно вынести за знак интеграла:

Замена переменной

Пусть x – функция от переменной t , x = φ(t) , тогда
.
Или наоборот, t = φ(x) ,
.

С помощью замены переменной можно не только вычислить простые интегралы, но и упростить вычисление более сложных.

Правило интегрирования по частям

Интегрирование дробей (рациональных функций)

Введем обозначение. Пусть P_k(x), Q_m(x), R_n(x) обозначают многочлены степеней k, m, n , соответственно, относительно переменной x .

Рассмотрим интеграл, состоящий из дроби многочленов (так называемая рациональная функция):

Если k ≥ n , то сначала нужно выделить целую часть дроби:
.
Интеграл от многочлена S_k-n(x) вычисляется по таблице интегралов.

Остается интеграл:
, где m .
Для его вычисления, подынтегральное выражение нужно разложить на простейшие дроби.

Для этого нужно найти корни уравнения:
Q_n(x) = 0 .
Используя полученные корни, нужно представить знаменатель в виде произведения сомножителей:
Q_n(x) = s (x-a) n_a (x-b) n_b . (x 2 +ex+f) n_e (x 2 +gx+k) n_g . .
Здесь s – коэффициент при x n , x 2 + ex + f > 0 , x 2 + gx + k > 0 , . .

После этого разложить дробь на простейшие:

Интегрируя, получаем выражение, состоящее из более простых интегралов.
Интегралы вида

приводятся к табличным подстановкой t = x – a .

Рассмотрим интеграл:

Преобразуем числитель:
.
Подставляя в подынтегральное выражение, получаем выражение, в которое входят два интеграла:
,
.
Первый, подстановкой t = x 2 + ex + f приводится к табличному.
Второй, по формуле приведения:

приводится к интегралу

Приведем его знаменатель к сумме квадратов:
.
Тогда подстановкой , интеграл

также приводится к табличному.

Интегрирование иррациональных функций

Введем обозначение. Пусть R( u₁, u₂, . , u_n ) означает рациональную функцию от переменных u₁, u₂, . , u_n . То есть
,
где P, Q – многочлены от переменных u₁, u₂, . , u_n .

Дробно-линейная иррациональность

Рассмотрим интегралы вида:
,
где – рациональные числа, m₁, n₁, . m_s, n_s – целые числа.
Пусть n – общий знаменатель чисел r₁, . r_s .
Тогда интеграл сводится к интегралу от рациональных функций подстановкой:
.

Интегралы от дифференциальных биномов

Рассмотрим интеграл:
,
где m, n, p – рациональные числа, a, b – действительные числа.
Такие интегралы сводятся к интегралам от рациональных функций в трех случаях.

1) Если p – целое. Подстановка x = t N , где N – общий знаменатель дробей m и n .
2) Если – целое. Подстановка a x n + b = t M , где M – знаменатель числа p .
3) Если – целое. Подстановка a + b x – n = t M , где M – знаменатель числа p .

Если ни одно из трех чисел не является целым числом, то по теореме Чебышева интегралы данного вида не могут быть выражены конечной комбинацией элементарных функций.

В ряде случаев, сначала бывает полезным привести интеграл к более удобным значениям m и p . Это можно сделать с помощью формул приведения:
;
.

Интегралы, содержащие квадратный корень из квадратного трехчлена

Здесь мы рассматриваем интегралы вида:
,

Подстановки Эйлера

Такие интегралы могут быть сведены к интегралам от рациональных функций одной из трех подстановок Эйлера:
, при a > 0 ;
, при c > 0 ;
, где x₁ – корень уравнения a x 2 + b x + c = 0 . Если это уравнение имеет действительные корни.

Тригонометрические и гиперболические подстановки

Также эти интегралы можно вычислить с помощью тригонометрических и гиперболических подстановок. В некоторых случаях этот способ вычисления интеграла является самым простым.
См. подробнее: Тригонометрические и гиперболические подстановки >>>

Прямые методы

В большинстве случаев, подстановки Эйлера приводят к более длинным вычислениям, чем прямые методы. С помощью прямых методов интеграл приводится к одному из перечисленных ниже видов.

I тип

Интеграл вида:
,
где P_n(x) – многочлен степени n .

Такие интегралы находятся методом неопределенных коэффициентов, используя тождество:

Дифференцируя это уравнение и приравнивая левую и правую части, находим коэффициенты A_i .

II тип

Интеграл вида:
,
где P_m(x) – многочлен степени m .

Подстановкой t = ( x – α ) –1 этот интеграл приводится к предыдущему типу. Если m ≥ n , то у дроби следует выделить целую часть.

III тип

Третий и наиболее сложный тип:
.

Здесь нужно сделать подстановку:
.
После чего интеграл примет вид:
.
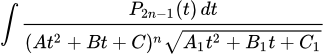
Далее, постоянные α, β нужно выбрать такими, чтобы коэффициенты при t обратились в нуль:
B = 0, B₁ = 0 .
Тогда интеграл распадается на сумму интегралов двух видов:
;
,
которые интегрируются, соответственно подстановками:
z 2 = A₁t 2 + C₁ ;
y 2 = A₁ + C₁ t –2 .

Общий случай

Самый общий интеграл вида:
,
сводится к интегралам трех предыдущих типов. Для этого достаточно, уничтожая иррациональность в знаменателе, преобразовать подынтегральную функцию к виду:
φ(x) + ψ(x)y ,
где φ(x), ψ(x) – рациональные функции от x , . Далее,
,
где ω(x) – рациональная дробь. В последнем интеграле рациональную дробь ω(x) можно преобразовать выделением целой части и разложением на простейшие дроби. После этого получаются интегралы трех рассмотренных типов.
См. подробнее: Интегрирование рациональной функции от квадратного корня из квадратного трехчлена >>>

Интегрирование трансцендентных (тригонометрических и показательных) функций

Заранее отметим, что те методы, которые применимы для тригонометрических функций, также применимы и для гиперболических функций. По этой причине мы не будем рассматривать интегрирование гиперболических функций отдельно.

Интегрирование рациональных тригонометрических функций от cos x и sin x

Рассмотрим интегралы от тригонометрических функций вида:
,
где R – рациональная функция. Сюда также могут входить тангенсы и котангенсы, которые следует преобразовать через синусы и косинусы.

При интегрировании таких функций полезно иметь в виду три правила:
1) если R( cos x, sin x ) умножается на –1 от перемены знака перед одной из величин cos x или sin x , то полезно другую из них обозначить через t .
2) если R( cos x, sin x ) не меняется от перемены знака одновременно перед cos x и sin x , то полезно положить tg x = t или ctg x = t .
3) подстановка во всех случаях приводит к интегралу от рациональной дроби. К сожалению, эта подстановка приводит к более длинным вычислениям чем предыдущие, если они применимы.

Произведение степенных функций от cos x и sin x

Рассмотрим интегралы вида:

Если m и n – рациональные числа, то одной из подстановок t = sin x или t = cos x интеграл сводится к интегралу от дифференциального бинома.

Если m и n – целые числа, то интегралы вычисляются интегрированием по частям. При этом получаются следующие формулы приведения:

Интегрирование по частям

Интегралы, содержащие логарифм или обратные тригонометрические функции:
ln φ , arcsin φ , arctg φ , и т.д., где φ – некоторая алгебраическая функция от x , нередко интегрируются по частям, полагая u = ln φ , u = arcsin φ , u = arctg φ , и т.д.
Подробнее: Примеры решения интегралов по частям, содержащих логарифм и обратные тригонометрические функции >>>

Применение формулы Эйлера

Если подынтегральное выражение линейно относительно одной из функций
cos ax или sin ax , то удобно применить формулу Эйлера:
e iax = cos ax + i sin ax (где i 2 = – 1 ),
заменив эту функцию на e iax и выделив действительную (при замене cos ax ) или мнимую часть (при замене sin ax ) из полученного результата.

Таким способом удобно находить интегралы вида
, ,
где P(x) – многочлен от x .
См. подробнее: Интегрирование произведения многочлена, экспоненты и синуса или косинуса >>>

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 27-09-2014

Источник

Методы решения неопределенных интегралов

1. Метод непосредственного интегрирования

Приведение к табличному виду или метод непосредственного интегрирования. С помощью тождественных преобразований подынтегральной функции интеграл сводится к интегралу, к которому применимы основные правила интегрирования и возможно использование таблицы основных интегралов.

Задание. Найти интеграл $\int 2^ <3 x-1>d x$

Решение. Воспользуемся свойствами интеграла и приведем данный интеграл к табличному виду.

$\int 2^ <3 x-1>d x=\int 2^ <3 x>\cdot 2^ <-1>d x=\frac<1> <2>\int\left(2^<3>\right)^ d x=$

Ответ. $\int 2^ <3 x-1>d x=\frac<8^><2 \ln 8>+C$

Подробнее о данном методе решении интегралов по ссылке →

2. Внесение под знак дифференциала

В формуле неопределенного интеграла величина $d x$ означает, что берется дифференциал от переменной $x$. Можно использовать некоторые свойства дифференциала, чтобы, усложнив выражение под знаком дифференциала, тем самым упростить нахождение самого интеграла. Для этого используется формула

Если нужная функция $y(x)$ отсутствует, иногда ее можно образовать путем алгебраических преобразований.

Методы решения неопределенных интегралов не по зубам? Тебе ответит эксперт через 10 минут!

Задание. Внесением под дифференциал найти неопределенный интеграл $\int \cos (2 x) d x$

Решение. Внесем 2$x$ под знак дифференциала, тем самым приведя исходный интеграл к табличному.

$\int \cos (2 x) d x=\int \cos (2 x) \cdot \frac<1> <2>\cdot 2 \cdot d x=\int \cos (2 x) \cdot \frac<1> <2>\cdot d(2 x)=$

$=\frac<1> <2>\int \cos (2 x) d(2 x)=\frac<1> <2>\int d(\sin 2 x)=\frac<1> <2>\sin 2 x+C$

Ответ. $\int \cos (2 x) d x=\frac<1> <2>\sin 2 x+C$

В общем виде справедливо равенство:

$\int f(y(x)) \cdot y^<\prime>(x) d x=\int f(y(x)) d(y(x))$

Задание. Найти интеграл $\int \frac<3-5 x>$

Решение. Внесем $3-5 x$ под знак дифференциала, тем самым приведя исходный интеграл к табличному.

Ответ. $\int \frac<3-5 x>=-\frac<1> <5>\ln |3-5 x|+C$

Подробнее о данном методе решении интегралов по ссылке →

3. Интегрирование заменой переменной

Интегрирование заменой переменной или методом подстановки. Пусть $x=\phi(t)$, где функция $\phi(t)$ имеет непрерывную производную $\phi^<\prime>(t)$, а между переменными $x$ и $t$ существует взаимно однозначное соответствие. Тогда справедливо равенство

$\int f(x) d x=\int f(\phi(t)) \cdot \phi^<\prime>(t) \cdot d t$

Определенный интеграл зависит от переменной интегрирования, поэтому если выполнена замена переменных, то обязательно надо вернуться к первоначальной переменной интегрирования.

Задание. Найти интеграл $\int \frac<3-5 x>$

Решение. Заменим знаменатель на переменную $t$ и приведем исходный интеграл к табличному.

Ответ. $\int \frac<3-5 x>=-\frac<1> <5>\ln |3-5 x|+C$

Подробнее о данном методе решении интегралов по ссылке →

4. Интегрирование по частям

Интегрированием по частям называют интегрирование по формуле

$\int u d v=u v-\int v d u$

При нахождении функции $v$ по ее дифференциалу $d v$ можно брать любое значение постоянной интегрирования $C$, так как она в конечный результат не входит. Поэтому для удобства будем брать $C=0$ .

Использование формулы интегрирования по частям целесообразно в тех случаях, когда дифференцирование упрощает один из сомножителей, в то время как интегрирование не усложняет другой.

Задание. Найти интеграл $\int x \cos x d x$

Решение. В исходном интеграле выделим функции $u$ и $v$, затем выполним интегрирование по частям.

$$\int x \cos x d x\left\|\begin u=x & v=\sin x \\ d u=d x & d v=\cos x d x \end\right\|=x \sin x-\int \sin x d x=$$

Ответ. $\int x \cos x d x=x \sin x+\cos x+C$

Подробнее о данном методе решении интегралов по ссылке →

Источник

Методы интегрирования

Вычислить первообразные функции мы можем не всегда, но задача на дифференцирование может быть решена для любой функции. Именно поэтому единого метода интегрирования, который можно использовать для любых типов вычислений, не существует.

В рамках данного материала мы разберем примеры решения задач, связанных с нахождением неопределенного интеграла, и посмотрим, для каких типов подынтегральных функций подойдет каждый метод.

Метод непосредственного интегрирования

Основной метод вычисления первообразной функции – это непосредственное интегрирование. Это действие основано на свойствах неопределенного интеграла, и для вычислений нам понадобится таблица первообразных. Прочие методы могут лишь помочь привести исходный интеграл к табличному виду.

Вычислите множество первообразных функции f ( x ) = 2 x + 3 2 · 5 x + 4 3 .

Решение

Для начала изменим вид функции на f ( x ) = 2 x + 3 2 · 5 x + 4 3 = 2 x + 3 2 · 5 x + 4 1 3 .

Мы знаем, что интеграл суммы функций будет равен сумме этих интегралов, значит:

∫ f ( x ) d x = ∫ 3 2 · 5 x + 4 3 = 2 x + 3 2 · 5 x + 4 1 3 d x = ∫ 3 2 · 5 x + 4 1 3 d x

Выводим за знак интеграла числовой коэффициент:

∫ f ( x ) d x = ∫ 2 x d x + ∫ 3 2 ( 5 x + 4 ) 1 3 d x = = ∫ 2 x d x + 2 3 · ∫ ( 5 x + 4 ) 1 3 d x

Чтобы найти первый интеграл, нам нужно будет обратиться к таблице первообразных. Берем из нее значение ∫ 2 x d x = 2 x ln 2 + C 1

Чтобы найти второй интеграл, потребуется таблица первообразных для степенной функции ∫ x p · d x = x p + 1 p + 1 + C , а также правило ∫ f k · x + b d x = 1 k · F ( k · x + b ) + C .

Следовательно, ∫ f ( x ) d x = ∫ 2 x d x + 3 2 · ∫ 5 x + 4 1 3 d x = = 2 x ln 2 + C 1 + 3 2 · 3 20 · ( 5 x + 4 ) 4 3 + C 2 = = 2 x ln 2 + 9 40 · 5 x + 4 4 3 + C

У нас получилось следующее:

∫ f ( x ) d x = ∫ 2 x d x + 3 2 · ∫ 5 x + 4 1 3 d x = = 2 x ln 2 + C 1 + 3 2 · 3 20 · ( 5 x + 4 ) 4 3 + C 2 = = 2 x ln 2 + 9 40 · 5 x + 4 4 3 + C

причем C = C 1 + 3 2 C 2

Ответ: ∫ f ( x ) d x = 2 x ln 2 + 9 40 · 5 x + 4 4 3 + C

Непосредственному интегрированию с применением таблиц первообразных мы посвятили отдельную статью. Рекомендуем вам ознакомиться с ней.

Метод подстановки

Такой метод интегрирования заключается в выражении подынтегральной функции через новую переменную, введенную специально для этой цели. В итоге мы должны получить табличный вид интеграла или просто менее сложный интеграл.

Этот метод очень полезен, когда нужно интегрировать функции с радикалами или тригонометрические функции.

Вычислите неопределенный интеграл ∫ 1 x 2 x — 9 d x .

Решение

Добавим еще одну переменную z = 2 x — 9 . Теперь нам нужно выразить x через z :

z 2 = 2 x — 9 ⇒ x = z 2 + 9 2 ⇒ d x = d z 2 + 9 2 = z 2 + 9 2 ‘ d z = 1 2 ·2 z d z = z d z

Далее подставляем полученные выражения в исходный интеграл и получаем:

∫ d x x 2 x — 9 = ∫ z d z z 2 + 9 2 · z = 2 ∫ d z z 2 + 9

Берем таблицу первообразных и узнаем, что 2 ∫ d z z 2 + 9 = 2 3 a r c t g z 3 + C .

Теперь нам нужно вернуться к переменной x и получить ответ:

2 3 a r c t g z 3 + C = 2 3 a r c t g 2 x — 9 3 + C

Ответ: ∫ 1 x 2 x — 9 d x = 2 3 a r c t g 2 x — 9 3 + C .

Если нам приходится интегрировать функции с иррациональностью вида x m ( a + b x n ) p , где значения m , n , p являются рациональными числами, то важно правильно составить выражение для введения новой переменной. Подробнее об этом читайте в статье, посвященной интегрированию иррациональных функций.

Как мы говорили выше, метод подстановки удобно использовать, когда требуется интегрировать тригонометрическую функцию. Например, с помощью универсальной подстановки можно привести выражение к дробно рациональному виду.

Этот метод объясняет правило интегрирования ∫ f ( k · x + b ) d x = 1 k · F ( k · x + b ) + C .

Добавляем еще одну переменную z = k · x + b . У нас получается следующее:

x = z k — b k ⇒ d x = d z k — b k = z k — b k ‘ d z = d z k

Теперь берем получившиеся выражения и добавляем их в интеграл, заданный в условии:

∫ f ( k · x + b ) d x = ∫ f ( z ) · d z k = 1 k · ∫ f ( z ) d z = = 1 k · F z + C 1 = F ( z ) k + C 1 k

Если же мы примем C 1 k = C и вернемся к исходной переменной x , то у нас получится:

F ( z ) k + C 1 k = 1 k · F k x + b + C

Метод подведения под знак дифференциала

Это метод основывается на преобразовании подынтегрального выражения в функцию вида f ( g ( x ) ) d ( g ( x ) ) . После этого мы выполняем подстановку, вводя новую переменную z = g ( x ) , находим для нее первообразную и возвращаемся к исходной переменной.

∫ f ( g ( x ) ) d ( g ( x ) ) = g ( x ) = z = ∫ f ( z ) d ( z ) = = F ( z ) + C = z = g ( x ) = F ( g ( x ) ) + C

Чтобы быстрее решать задачи с использованием этого метода, держите под рукой таблицу производных в виде дифференциалов и таблицу первообразных, чтобы найти выражение, к которому надо будет приводится подынтегральное выражение.

Разберем задачу, в которой нужно вычислить множество первообразных функции котангенса.

Вычислите неопределенный интеграл ∫ c t g x d x .

Решение

Преобразуем исходное выражение под интегралом с помощью основных тригонометрических формул.

c t g x d x = cos s d x sin x

Смотрим в таблицу производных и видим, что числитель можно подвести под знак дифференциала cos x · d x = d ( sin x ) , значит:

c t g x d x = cos x d x sin x = d sin x sin x , т.е. ∫ c t g x d x = ∫ d sin x sin x .

Допустим, что sin x = z , в таком случае ∫ d sin x sin x = ∫ d z z . Согласно таблице первообразных, ∫ d z z = ln z + C . Теперь вернемся к исходной переменной ∫ d z z = ln z + C = ln sin x + C .

Все решение в кратком виде можно записать так:

∫ с t g x d x = ∫ cos x d x sin x = ∫ d sin x sin x = s i n x = t = = ∫ d t t = ln t + C = t = sin x = ln sin x + C

Ответ: ∫ с t g x d x = ln sin x + C

Метод подведения под знак дифференциала очень часто используется на практике, поэтому советуем вам прочесть отдельную статью, посвященную ему.

Метод интегрирования по частям

Этот метод основывается на преобразовании подынтегрального выражения в произведение вида f ( x ) d x = u ( x ) · v ‘ x d x = u ( x ) · d ( v ( x ) ) , после чего применяется формула ∫ u ( x ) · d ( v ( x ) ) = u ( x ) · v ( x ) — ∫ v ( x ) · d u ( x ) . Это очень удобный и распространенный метод решения. Иногда частичное интегрирование в одной задаче приходится применять несколько раз до получения нужного результата.

Разберем задачу, в которой нужно вычислить множество первообразных арктангенса.

Вычислите неопределенный интеграл ∫ a r c t g ( 2 x ) d x .

Решение

Допустим, что u ( x ) = a r c t g ( 2 x ) , d ( v ( x ) ) = d x , в таком случае:

d ( u ( x ) ) = u ‘ ( x ) d x = a r c t g ( 2 x ) ‘ d x = 2 d x 1 + 4 x 2 v ( x ) = ∫ d ( v ( x ) ) = ∫ d x = x

Когда мы вычисляем значение функции v ( x ) , прибавлять постоянную произвольную С не следует.

Далее используем формулу интегрирования по частям и получаем:

∫ a r c t g ( 2 x ) d x = u ( x ) · v ( x ) — ∫ v ( x ) d ( u ( x ) ) = = x · a r c t g ( 2 x ) — ∫ 2 x d x 1 + 4 x 2

Получившийся интеграл вычисляем, используя метод подведения под знак дифференциала.

Поскольку ∫ a r c t g ( 2 x ) d x = u ( x ) · v ( x ) — ∫ v ( x ) d ( u ( x ) ) = x · a r c t g ( 2 x ) — ∫ 2 x d x 1 + 4 x 2 , тогда 2 x d x = 1 4 d ( 1 + 4 x 2 ) .

∫ a r c t g ( 2 x ) d x = x · a r c t g ( 2 x ) — ∫ 2 x d x 1 + 4 x 2 = = x · a r c t g ( 2 x ) — 1 4 ln 1 + 4 x 2 + C 1 = = x · a r c t g ( 2 x ) — 1 4 ln 1 + 4 x 2 + C

Ответ: ∫ a r c t g ( 2 x ) d x = x · a r c t g ( 2 x ) — 1 4 ln 1 + 4 x 2 + C .

Главная сложность применения такого метода – это необходимость выбирать, какую часть брать за дифференциал, а какую – за функцию u ( x ) . В статье, посвященной методу интегрирования по частям, даны некоторые советы по этому вопросу, с которыми следует ознакомиться.

Если нам требуется найти множество первообразных дробно рациональной функции, то нужно сначала представить подынтегральную функцию в виде суммы простейших дробей, а потом интегрировать получившиеся дроби. Подробнее см. статью об интегрировании простейших дробей.

Если мы интегрируем степенное выражение вида sin 7 x · d x или d x ( x 2 + a 2 ) 8 , то нам будут полезны рекуррентные формулы, которые могут постепенно понижать степень. Они выводятся с помощью последовательного многократного интегрирования по частям. Советуем прочитать статью «Интегрирование с помощью рекуррентных формул.

Подведем итоги. Для решения задач очень важно знать метод непосредственного интегрирования. Другие методы (подведение под знак дифференциала, подстановка, интегрирование по частям) также позволяют упростить интеграл и привести его к табличному виду.

Источник