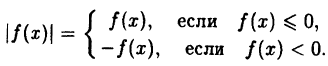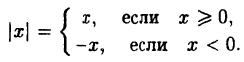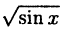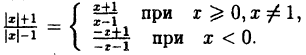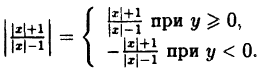- Растяжение и сжатие графиков функций
- Список функций, изученных в 7 и 8 классе
- Растяжение и сжатие графика по оси OX
- Растяжение и сжатие графика по оси OY
- Примеры
- Преобразования графиков функций с примерами решения и образцами выполнения
- Параллельный перенос графиков
- Сжатие и растяжение графиков
- Построение графиков с модулями
- Построение графиков функций с примерами
Растяжение и сжатие графиков функций
Список функций, изученных в 7 и 8 классе
Растяжение и сжатие графика по оси OX
Сравним графики пар функций, которые в общем виде можно записать так:
$$ y_1 = f(x), y_2 = f(px) $$
где $p \gt 1$, произвольный положительный множитель.
$ y_2 = f(2x) = (2x)^2 = 4x^2 $
$y_2 = y_1 при x_2 = \frac<1> <2>x_1$
График сжимается в 2 раза по оси OX

$ y_2 = y_1 при x_2 = \frac<1> <2>x_1 $
График сжимается в 2 раза по оси OX
$y_2=y_1 при x_2 = \frac<1> <2>x_1$
График сжимается в 2 раза по оси OX
Теперь сравним пары функций с делением на p:
$$ y_1 = f(x), \quad y_2 = f \left( \frac
\right), \quad p \gt 1 $$
$ y_2 = f \left(\frac
$y_2 = y_1 при x_2 = 2x_1$
График растягивается в 2 раза по оси OX

$y_2 = f \left(\frac
$ y_2 = y_1 при x_2 = 2x_1$
График растягивается в 2 раза по оси OX
$y_2=y_1 при x_2 = 2x_1$
График растягивается в 2 раза по оси OX
При сравнении графиков двух функций
$$ y_1 = f(x), \quad y_2 = f(px), \quad p \gt 1 $$
график второй функции сжимается в p раз по оси OX по сравнению с графиком первой функции.
При сравнении графиков двух функций
$$ y_1 = f(x), \quad y_2 = f \Biggl(\frac
\Biggr), \quad p \gt 1 $$
график второй функции растягивается в p раз по оси OX по сравнению с графиком первой функции.
Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)
Растяжение и сжатие графика по оси OY
Сравним графики пар функций, которые в общем виде можно записать так:
$$ y_1 = f(x), \quad y_2 = Af(x) $$
где $A \gt 1$, произвольный положительный множитель.
$y_2 = 2y_1 при x_2 = x_1$
График растягивается в 2 раза по оси OY

$ y_2 = 2y_1 при x_2 = x_1$
График растягивается в 2 раза по оси OY
$y_2 = 2f(x) = 2\sqrt
$y_2 = 2y_1 при x_2 = x_1$
График растягивается в 2 раза по оси OY
Теперь сравним пары функций с делением на A:
$y_2 = \frac<1><2>y_1 при x_2 = x_1$
График сжимается в 2 раза по оси OY

$ y_2 = \frac<1><2>y_1 при x_2 = x_1$
График сжимается в 2 раза по оси OY
$y_2 = \frac<1><2>y_1 при x_2 = x_1$
График сжимается в 2 раза по оси OY
При сравнении графиков двух функций
$$ y_1 = f(x), \quad y_2 = Af(x), \quad A \gt 1 $$
график второй функции растягивается в A раз по оси OY по сравнению с графиком первой функции.
При сравнении графиков двух функций
график второй функции сжимается в A раз по оси OY по сравнению с графиком первой функции.
Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)
Примеры
Пример 1. Постройте в одной координатной плоскости графики функций:
По сравнению с графиком $y = \sqrt
- график функции $y = \sqrt<3x>$ сжимается в 3 раза по оси OX(←)
- график функции $y = \sqrt<\frac
<3>>$ растягивается в 3 раза по оси OX(→) - график функции $y = 3\sqrt
$ растягивается в 3 раза по оси OY(↑)
Пример 2*. Постройте в одной координатной плоскости графики функций:
$$ y = f(x), y = f(2x), y = f \Biggl(\frac
Исходная функция $y = f(x) = x^2+3x+2$
$$ y = f(2x) = (2x)^2+3 \cdot (2x)+2 = 4x^2+6x+2 $$
$$ y = f\Biggl(\frac
По сравнению с графиком $y = f(x) = x^2+3x+2$:
- график функции y = f(2x) сжимается в 2 раза по оси OX(→)
- график функции $y = f \left(\frac
<2>\right)$ растягивается в 2 раза по оси OX(←) - график функции y = 2f(x) растягивается в 2 раза по оси OY(↑)
Источник
Преобразования графиков функций с примерами решения и образцами выполнения
Параллельный перенос, сжатие и растяжение графиков. Построение графиков с модулями.
Графики многих функций можно получить из ранее рассмотренных с помощью элементарных геометрических преобразований: параллельного переноса, сжатия, растяжения, симметричного отображения. Рассмотрим некоторые из этих преобразований. Для каждого из элементарных преобразований предлагается два способа построения графика: с помощью преобразования графика и с помощью преобразования системы координат. Обучающийся должен выбрать тот, который кажется ему проще и овладеть им. В каждом случае считается известным график функции у = f(х).
Параллельный перенос графиков
График функции у = /(x) + Ь получается из графика функции у = f(х) с помощью его переноса на вектор b = (0; b). Действительно, в этом случае ко всем ординатам графика у = f(х) прибавляется величина b, что означает сдвиг графика вдоль оси Оу. Если b > 0, то график функции у = f(х) переносится вверх параллельно оси Oy на b, если b 0 — вниз, если b 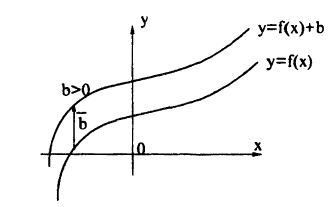
Пример:
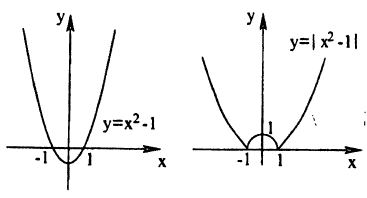
График функции у = x² — 1 (рис. 50) смещен на 1 вниз параллельно оси Oy относительно графика функции у = х².
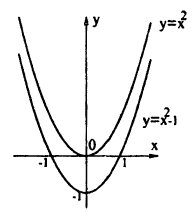
График функции у = f(x+a) получается с помощью переноса графика функции у = f(x) на вектор а = (—а;0). Действительно, перейдя к новым координатам X = х + α, Y = у параллельным переносом вдоль оси Ox на —а, заметим, что относительно новых координат получится исходный график функции Y = f(X). Если а > 0, то старые координаты получаются из новых сдвигом направо вдоль оси Ox на α, т.к. х = X — а. Если же сдвигать график, а не систему координат, то его нужно двигать в противоположном направлении — налево. Итак, если а > 0, то график функции у = f(x) переносится налево параллельно оси Ox на а, если а 0 — вправо, если α 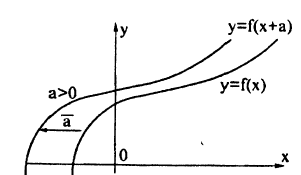
Сжатие и растяжение графиков
График функции у = kf(x), где к ∈ R, получается с помощью ’’растяжения” графика функции у = f(x) в к раз в направлении от оси Ох. ’’Растяжение” здесь понимается как умножение на к ординат всех точек графика у = f(x)∙ При k > 1 это будет действительно растяжение в к раз от оси Ox вдоль оси Оу. При 0 0 можно исправить значения по оси Оу, умножив их на k. При k 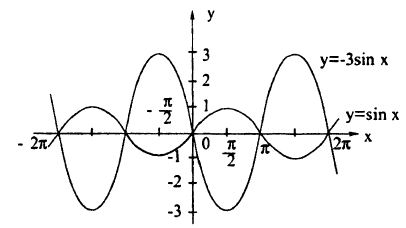
При k > 1 график функции у = f(x) сжимается в k раз к оси Oy вдоль оси Ох; при 0 0 можно исправить значения по оси Ох, поделив их на k. При k 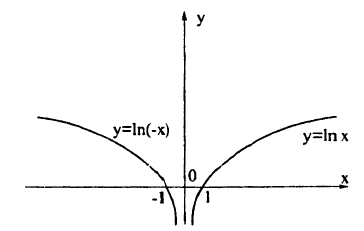
Пользуясь изложенными методами, приведем последовательность преобразований при построении графика функции у = f(kx + b), если дан график функции у = f(x):
- нарисовать график функции у = f(x);
- получить график функции у = f(x + b), сдвинув исходный на вектор b = (-b; 0), как описано в п. 5.1;
- получить график функции у = f(kx + b), “сжав” предыдущий в к раз к оси Оу, как описано выше.
Пример:
Написать последовательность преобразований и построить график функции у = 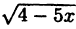
Решение:
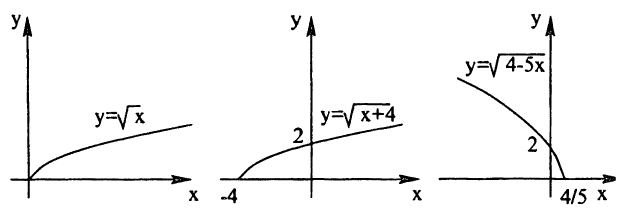
- нарисуем график функции у = √х;
- о получим график функции у =
, сдвинув исходный на 4 единицы влево вдоль оси Ох;
- о получим график функции у =
, сжав предыдущий в 5 раз к оси Oy и затем отобразив симметрично относительно оси Оу.
Построение графика показано на рис. 55
Замечание:
Теперь понятно, что если функция у = f(x) периодическая с периодом Т, то функция у = К ∙ f(kx + b) + а тоже периодическая с периодом T₁ = 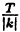
Построение графиков с модулями
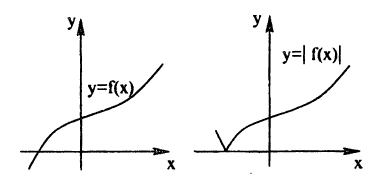
График функции у = ∣f(x)∣ получается из графика функции у = f(x) следующим образом (рис. 56)
- все части графика функции у = f(x), лежащие ниже оси Ох, следует отобразить вверх симметрично относительно этой оси;
- оставшиеся внизу части исходного графика следует стереть.
Действительно, по определению модуля действительного числа имеем:
(5.1)
Таким образом, те участки исходного графика, которые лежат не ниже оси Ox (f(x) ≥ 0), менять не нужно, а для тех участков, которые лежат ниже оси Ох, нужно построить функцию у = —f(x). В соответствии с п. 5.2 это получается симметричным отображением исходного графика относительно оси Ох. Заметим, что полученный график лежит не ниже оси Ох, что естественно, т.к. |f(x)| ≥ 0 для ∀x ∈ D(f).
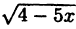
Пример:
Построение графика функции у = |х² — 1| показано на рис. 57.
График функции у = f (|x|) получается из графика функции у = f(х) следующим образом (рис. 58):
- все части графика функции у = f(x), лежащие слева от оси Оу, следует стереть;
- о оставшуюся часть графика следует отобразить налево симметрично относительно оси Оу.
Действительно, по определению модуля действительного числа имеем:
(5.2)
Таким образом, не нужно изменять те участки исходного графика, для которых х ≥ 0, а для х 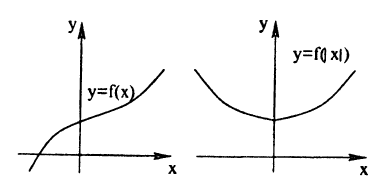
Пример:
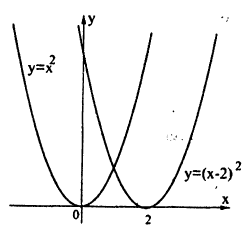
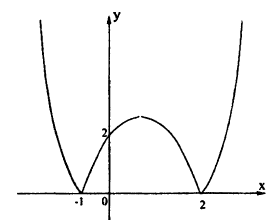
Построение графика функции у = (|x| — 2)² показано на рис. 59
Элементарными методами можно строить эскизы графиков более сложных функций.
Пример:
Построить эскиз графика у =
Решение:
Построение графика показано на рис. 60. Заметим, что график отсутствует там, где sin х 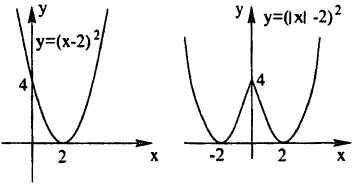
Кроме того, так как √u > и при 0 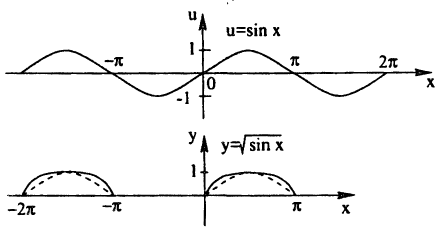
Построение графиков функций с примерами
Пример:
C помощью элементарных преобразований постройте график функции: у = x² — х — 2.
Решение:
Выделим полный квадрат из правой части уравнения функции: у = x² — х — 2 ⇔ y = x²-x+ 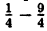
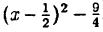
1) y =x²
2) у =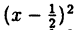
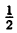
3) у = 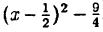
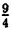
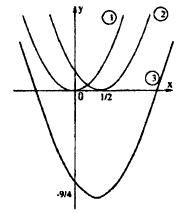
Пример:
Используя сложение, деление функций, постройте график функции: у = х + 
Решение:
В одних осях координат нарисуем графики следующих функций (рис. 62):
1) у = х,
2) y=
3) y = x + 
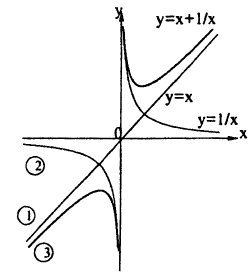
Пример:
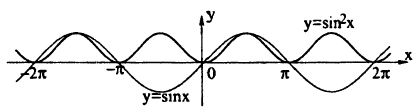
Постройте график сложной функции у = sin² х.
Решение:
В одних осях координат нарисуем графики функций:
1) y = sin x,
2) y = sin² х.
Учитывая, что квадрат числа меньшего единицы, меньше исходного числа, получим график (рис. 63)
Пример:
Постройте график функции в полярной системе координат: r = 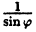
Решение:
Вычислим значения г для некоторых значений 
 | 0 | 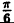 | 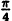 | 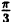 | 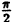 |
| r | ∞ | 2 | 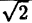 | 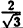 | ∞ |
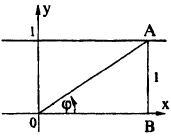
Соединив плавной линией найденные точки, получим линию вдоль оси Ох, проходящую через точку (0;1). Докажем что эта линия — прямая (рис. 64). Действительно: из Δ ОAВ ⇒ cos 
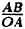
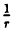
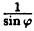
Пример:
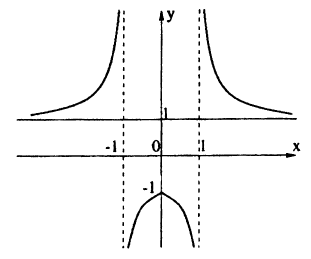
Постройте линию, описываемую уравнением, у =
Решение:
Сначала построим график функции у = 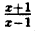
Наконец, строим линию описываемую уравнением у = 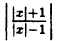
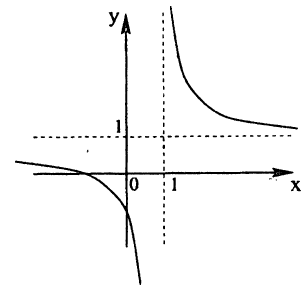
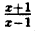
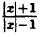
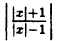
Пример:
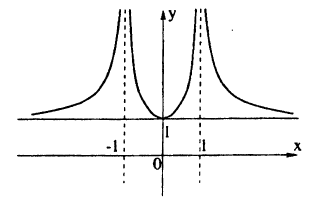
Постройте линию, описываемую уравнением у =
Решение:
Для построения графика данного примера сначала постройте график функции у =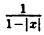
Пример:
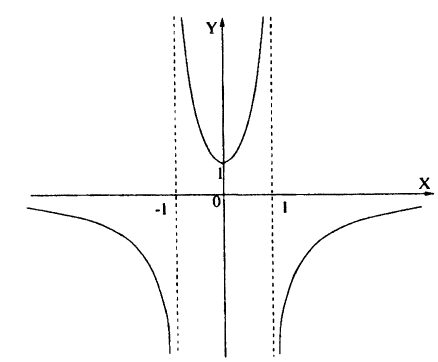
Постройте линию, описываемую уравнением у = |х² — х -2|.
Решение:
Для построения графика данного примера сначала постройте график функции у = х² — х — 2. Затем отразите симметрично оси Ox ту часть графика, которая осталась снизу от оси Ох. Затем сотрите ту часть графика, которая расположена в нижней полуплоскости.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Источник












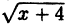 , сдвинув исходный на 4 единицы влево вдоль оси Ох;
, сдвинув исходный на 4 единицы влево вдоль оси Ох;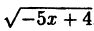 , сжав предыдущий в 5 раз к оси Oy и затем отобразив симметрично относительно оси Оу.
, сжав предыдущий в 5 раз к оси Oy и затем отобразив симметрично относительно оси Оу.