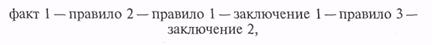1.3.Представление знаний в интеллектуальных системах
Человек одновременно использует самые различные методы представления знаний: языковое описание, графическая информация, математические формулы и т.д. В зависимости от специфики той или иной области деятельности один или несколько видов описания будут превалировать над остальными. Например, в математике формулы и графики будут преобладать над текстовой информацией, в юриспруденции доминирует текстовая информация, в искусствоведении преобладает текстовая и графическая информация. В случае выбора средств представления знаний в технических системах такой универсализм представления знаний невозможен, поскольку потребует аппаратной и программной реализации интеллектуальных функций, недостижимых в настоящее время. Поэтому, существует несколько базовых специализированных машинных языков представления знаний, каждый из которых наиболее предпочтителен для той или иной предметной области [10] — [14] .
1) Язык продукционных правил.
Продукционные правила – это правила, имеющие форму: ЕСЛИ «Условие» – ТО «Событие». Продукционные правила описывают знания в виде взаимосвязей типа: «причина» – «следствие», «явление» – «реакция», «признак» – «факт» и.т.п. Конкретизация продукционных правил меняется в зависимости от сущности представляемых знаний.
- ЕСЛИ «Температура в реакторе превышает 120 ° C » ТО «Снизить подачу топлива на 5%»;
- ЕСЛИ «Вышел из строя вентилятор кондиционера» ТО «Температура в помещении повышается»;
Продукционное представление знаний с человеческой точки зрения является прямым описанием логических выводов при решении конкретных задач. Совокупность знаний о конкретной предметной области в этом случае представляется соответствующим набором продукционных правил, который образует базу знаний. При построении продукционных правил допустимо использование логических операторов И, ИЛИ, например:
- ЕСЛИ «Температура в реакторе превышает 120 ° C » И «Температура хладагента превышает 90 ° C » ТО «Прекратить подачу топлива»;
- ЕСЛИ «Температура в реакторе превышает 90 ° C » ИЛИ «Температура хладагента превышает 60 ° C » ТО «Снизить подачу топлива на 40%».
Недостатком языка продукционных правил можно считать отсутствие явных связей между правилами и целями, к достижению которых необходимо стремится. Таким образом, для активизации одного из продукционных правил необходимо проверка всей продукционной базы знаний, что при больших объемах информации приводит к существенным затратам временных и технических ресурсов интеллектуальной системы. Возможность решения этой проблемы заключается в разработке перспективных продукционных баз знаний, в которых одни продукционные правила могут активировать и дезактивировать другие продукционные правила, влияя на количество перебираемых правил в текущем цикле и, следовательно, на выбор пути достижения цели управления.
Отличительной чертой и основным преимуществом продукционной базы знаний является простота анализа, дополнения, модификации и аннулирования определенных продукционных правил. Помимо этого, представление знаний в таком синтаксически однотипном виде существенно облегчает техническую реализацию системы использования знаний. Вследствие этого в настоящее время продукционные базы знаний получили наибольшее распространение в интеллектуальных технических системах.
2) Язык семантических сетей.
Знаниями можно назвать описания отношений между абстрактными понятиями и сущностями, являющимися конкретными объектами реального мира. Изначально семантические сети разрабатывались как модели долговременной человеческой памяти в психологии, но впоследствии эта модель перекочевала в инженерию знаний. В семантической сети абстрактные понятия и отношения между ними описываются в виде узлов и дуг. Сущности и понятия в такой сети являются узлами, а отношения между ними – дугами. Атрибуты семантических сетей можно разделить на лингвистические (объект, условие, место, инструмент, цель и т.п.), атрибутивные (форма, размер, цвет и т.п.), характеристические (род, время, наклонение и т.п.), логические (да, нет, отрицание, объединение и т.п.).
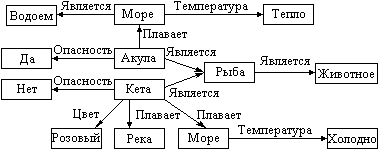
Рис.1.5. Семантическое представление знаний биолога
Допустим, фрагмент знаний ихтиолога о биологии рыб можно описать следующей семантической сетью (рис.1.5). В качестве другого примера рассмотрим представление знаний, содержащихся в высказывании: «Робот сверлит отверстие в детали с помощью сверла 10» (рис.1.6).
Рис.1.6. Семантическое представление технического знания
Недостаток семантических сетей – дублирование информации при построении сетей и смешение групп знаний, относящихся к различным ситуациям. Например, семантическая сеть, представленная на рис.1.5, имеет дубляж понятия «море», а отношение «температура» может использоваться не только для описания среды обитания животных. Выходом из данной ситуации стала наметившаяся в последнее время тенденция к построению разделенных семантических сетей.
Основным преимуществом семантических сетей является то, что они имитируют понимание и использование человеком естественного языка, что позволяет применять их при техническом моделировании рассуждений, доказательстве теорем, построении незаданных явно причинно-следственных связей и лингвистических конструкций, т.е. семантические сети позволяют реализовать устройства, имитирующие мыслительные акты более высокого уровня по сравнению с продукционными правилами. Представление знаний в виде семантических сетей широко используется в интеллектуальных системах интерпретации естественного языка и автоматического машинного перевода, в диалоговых вопросно-ответных системах естественного человеко-машинного общения, в блоках логической интерпретации систем технического зрения.
3) Язык логики предикатов.
Логика предикатов является разделом математики – математической логикой, имеющей большую историю. Данная область математики традиционно составляла математический фундамент, закладываемый в основу формального описания систем. В качестве примера построения и вывода знаний на языке логики предикатов достаточно привести известный силлогизм Сократа: Все люди – смертны, человек – один из людей, Сократ – человек, следовательно Сократ – смертен.
Основные положения логики предикатов заключаются в следующем. Допустим, имеется некоторое множество объектов, составляющих предметную область, знания о которой необходимо описать. Произвольные элементы этого множества называются предметными переменными x i , а конкретные элементы этого множества, называются предметными константами y i . Выражение P x 1 , x 2 , … , x n , зависящее от предметных переменных и принимающее значение «0»-(ложь) или «1»-(истина), называется логической функцией или предикатом. Выражение P y 1 , y 2 , … , y m , зависящее от предметных констант и принимающее значение «0»-(ложь) или «1»-(истина), называется элементарной формулой. Из элементарных формул с помощью логических связок « ∧ »-(И), « ∨ »-(ИЛИ), « ¬ »-(отрицание), « -(импликация), « ↔ »-(эквивалентность) строятся предикатные формулы. Помимо логических связок в рассмотрение вводят квантор общности и квантор существования « ∃ ». Знания о конкретной предметной области будут описываться предикатами и предикатными формулами. Для организации логического вывода « ↦ »-(символ выводимости) на языке логики предикатов используются различные правила. Например, правило Moduspones ( A → B , A ↦ B ) – если из A следует B и если A является логически непротиворечивой предикатной формулой, то B также является логически непротиворечивой предикатной формулой. В качестве примера рассмотрим основной набор базовых действий и производных правил поведения транспортного робота-тележки, записанные на языке исчисления предикатов:
A — «накопитель готовых деталей около станка пуст»;
B -«тележка транспортного робота пуста»;
C -«освободить накопитель готовых деталей около станка»;
D -«перейти к следующему станку»;
E -«отвезти детали на склад, освободить тележку робота»;
F -«вернуться к текущему станку»;
Основной недостаток языка логики предикатов при представлении знаний состоит в ограниченной выразимости, поскольку существует множество фактов и взаимосвязей, которые тяжело или даже невозможно выразить средствами математической логики. Например, такое логичное с точки зрения человека умозаключение, как «Человек колет дрова топором, топор – острый, следовательно человеку колоть дрова легко», на языке логики предикатов непредставимо, поскольку содержит так называемый сценарный, а не логический вывод.
Преимущество логики предикатов при представлении знаний заключается в том, что данный способ обладает хорошо развитым и понятным математическим аппаратом. Логика предикатов всесторонне исследована как формальная система. Синтаксис и интерпретация логических функций, элементарных и предикатных формул, правил логического вывода образуют единую стройную теорию математической логики. Это позволяет легко программировать различные операции над знаниями, в том числе логический вывод новых знаний на основе имеющихся знаний. Язык логики предикатов почти так же популярен в технических системах, как и язык продукционных правил, который можно рассматривать как упрощенный язык логики предикатов. Действительно, базовая конструкция языка продукционных правил: ЕСЛИ «причина»/«условие» ТО «следствие»/«действие», по сути является всего лишь одной из логических связок языка логики предикатов – импликацией A → B (из A следует B ). Однако, в отличие от языка логики предикатов, язык продукционных правил обладает одним существенным преимуществом – полной независимостью элементов базы знаний, поскольку отдельные продукционные правила логически не связаны между собой. Это, несмотря на некоторые осложнения при обработке знаний, обусловленные опасностью нарушения их целостности и непротиворечивости, позволяет языку продукционных правил охватить больший круг различных предметных областей за счет возможности описания знаний, опирающихся не на логические, а на традуктивные и сценарные выводы [1] , [10] , [13] . Поэтому по частоте использования в интеллектуальных системах язык логики предикатов на данный момент все таки немного уступает языку продукционных правил.
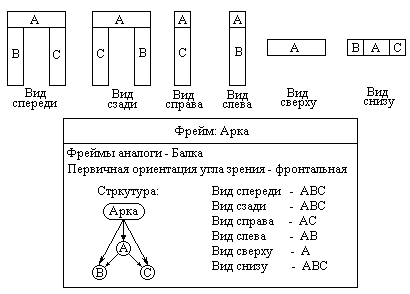
Фреймовая система представления знаний является моделью описания человеческих знаний в виде связанной совокупности крупных структурных единиц, каждая из которых содержит данные, описывающие определенную ситуацию. Во фреймовой системе единицей представления является объект, называемый фреймом. Фрейм содержит совокупность некоторых понятий и сущностей, с помощью которой можно описать конкретную ситуацию. Фрейм имеет уникальное имя и внутреннюю структуру, состоящую из множества упорядоченных элементов – слотов. Каждый слот имеет уникальное в пределах своего фрейма имя и содержит определенную информацию. Таким образом, каждый фрейм это структура данных, описывающая определенную ситуацию, место, объект и т.п. Структура данных внутри фрейма может иметь различный вид: граф, таблица и т.п., а также может представлять комбинацию различных способов представлений данных. Фреймы могут быть связаны между собой посредством своих слотов и образовывать иерархические структуры. Например, в системе технического зрения, имеющей три пары независимо пространственно ориентированных датчиков, составная арка может быть представлена в виде следующего фрейма (рис.1.7):
Рис.1.7. Фрейм, описывающий различные ракурсы обзора арки.
Описание арки таким фреймом, позволяет распознавать арку и ее ориентацию в системах технического зрения. Допустим, система технического зрения оценивает панораму арки при виде сверху. Результат оценки – «А». Далее система начинает сличать оценку «А» со значениями различных слотов в различных фреймах и составлять список фреймов- кандидатов на идентификацию детали. Результатом отбора будут описывающие различные конструкции фреймы, содержащие слот со значением «А». Системе остается изменить угол зрения, оценить новую панорамную картину и сузить список фреймов, проверяя на соответствие новому значению слоты первоначально отобранных фреймов. К примеру, фрейм – балка выпадет из списка после первой же процедуры отсева, поскольку как балку не крути, результат оценки панорамы всегда будет – «А». Последовательно повторяя этот процесс, можно идентифицировать деталь абсолютно точно (по всем шести ракурсам) или с определенной степенью вероятности (если ракурсов анализа меньше). Машина может идти и по другому пути анализа: не составлять список фреймов-кандидатов, а остановиться на первом попавшемся подходящем фрейме и провести сравнительную оценку всех ракурсов детали с соответствующими слотами фрейма. Если хотя бы один из слотов текущего фрейма противоречит оценке панорамы, то анализу подвергается фрейм-аналог и т.д., пока при движении по цепочке фреймов не будет достигнуто совпадение всех ракурсов, или их наибольшего числа.
Недостатком фреймовой системы является то, что иерархическая сеть знаний с перекрестными ссылками пригодна для решения сравнительно простых проблем, поскольку при расширении проблемной области фреймовая сеть имеет свойство разрастаться до значительных размеров. Проблемы поиска решения в таких сетях становятся трудноразрешимыми, поскольку связи между фреймами в сетях, описывающих объемные знания, как правило, неоднозначны и устанавливаются по нескольким слотам. Кроме того, фреймовые сети менее приспособлены к адаптации, так как внесение новых фреймов и измерение слотов в имеющихся фреймах может повлечь противоречия и зацикливания в ссылках при движении по иерархической структуре фреймовой сети.
Достоинством фреймового языка представления знаний является то, что он предоставляет пользователю большую свободу при описании знаний, так как допускает различные способы описания данных в пределах одного фрейма. Благодаря этому, фреймовые системы можно отнести к самым универсальным системам описания знаний. Однако ограничение сложности решаемых на основе таких систем проблем пока не позволяет фреймовым системам доминировать при разработке интеллектуальных систем.
Источник
Классификация методов представления знаний



Для того чтобы манипулировать всевозможными знаниями из реального мира с помощью компьютера, необходимо осуществить их моделирование.
При проектировании модели представления знаний следует учесть два требования: однородность представления; простоту понимания.
Выполнение этих требований позволяет упростить механизм логического вывода и процессы приобретения знаний и управления ими, однако, как правило, создателям интеллектуальной системы приходится идти на некоторый компромисс в стремлении обеспечить одинаковое понимание знаний и экспертами, и инженерами знаний, и пользователями.
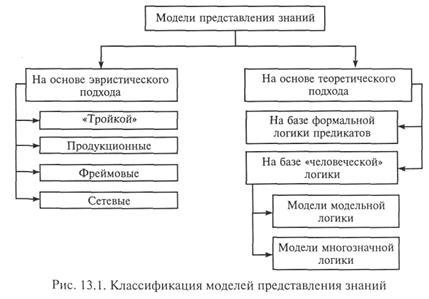
Классификация методов моделирования знаний с точки зрения подхода к их представлению в ЭВМ показана на рис. 13.1.
Дадим общую характеристику основных методов представления знаний.
Модели на основе эвристического подхода.Представление знаний тройкой «объект — атрибут — значение». Один из первых методов моделирования знаний. Как правило, используется для представления фактических знаний в простейших системах.
Очевидно, что для моделирования знаний даже об одном объекте (например, о «студенте» или «доме») из предметной области необходимо хранить значительное число «троек».
Продукционная модель. Модель правил; модель продукций — от англ. production — изготовление, выработка. В настоящее время наиболее проработанная и распространенная модель представления знаний, в частности в ЭС.
Модель предусматривает разработку системы продукционных правил (правил продукций), имеющих вид:
где Аi и Bj — некоторые высказывания, к которым применены логические операции И и ИЛИ. Если высказывания в левой части правила (ее часто называют антецедент — условие, причина) истинно, истинно и высказывание в правой части (консеквент — следствие).
Полнота базы знаний (базы правил) определяет возможности системы по удовлетворению потребностей пользователей. Логический вывод в продукционных системах основан на построении прямой и обратной цепочек заключений, образуемых в результате последовательного просмотра левых и правых частей соответствующих правил, вплоть до получения окончательного заключения.
Пусть в некоторой области памяти (базе знаний) хранятся следующие правила (суждения):
· правило 1: ЕСЛИ в стране происходит падение курса национальной валюты, ТО материальное положение населения ухудшается;
· правило 2: ЕСЛИ объемы производства в стране падают, ТО курс национальной валюты снижается;
· правило 3: ЕСЛИ материальное положение населения ухудшается, ТО уровень смертности в стране возрастает.
Если на вход системы поступит новый факт (факт 1) «В стране высокий уровень падения объемов производства», то из правил можно построить цепочку рассуждений и сформулировать два заключения:
где заключение 1 (промежуточный вывод) — «Материальное положение населения ухудшается»; заключение 2 (окончательный вывод) — «В стране возрастает уровень смертности».
Отметим, что в современных ЭС в базе знаний могут храниться тысячи правил, а коммерческая стоимость одного невыводимого (нового, дополнительного) правила весьма высока.
Главными достоинствами продукционных систем являются простота пополнения и изъятия правил; простота реализации механизма логического вывода и наглядность объяснений результатов работы системы.
Основной недостаток подобных систем — трудность обеспечения непротиворечивости правил при их большом числе, что требует создания специальных правил (так называемых метаправил) разрешения возникающих в ходе логического вывода противоречий. Кроме того, время формирования итогового заключения может быть достаточно большим.
Фреймовая модель. Сравнительно новая модель представления знаний. Само понятие «фрейм» (англ. frame — рама, рамка, скелет, сгусток, сруб и т.д.) было введено в 1975 г. М.Минским (M.Minsky, США).
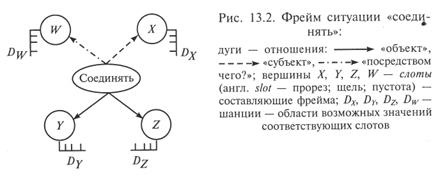
Фрейм — это минимальная структура информации, необходимая для представления знаний о стереотипных классах объектов, явлений, ситуаций, процессов и др. С помощью фреймов можно моделировать знания о самых разнообразных объектах интересующей исследователя предметной области — важно лишь, чтобы эти объекты составляли класс концептуальных (повторяющихся: стереотипных) объектов, процессов и т. п. Примерами стереотипных жизненных ситуаций могут служить собрание, совещание; сдача экзамена или зачета; защита курсовой работы и др. Примеры стереотипных бытовых ситуаций: отъезд в отпуск, встреча гостей, выбор телевизора, ремонт и др. Примеры стереотипных понятий: алгоритм; действие; методика и др. На рис. 13.2 представлен фрейм технологической операции «соединять» [21].

Данный фрейм описывает ситуацию «Субъект X соединяет объект Y с объектом Z способом W».
Наполняя слоты конкретным содержанием, можно получить фрейм конкретной ситуации, например: «Радиомонтажник соединяет микросхему с конденсатором способом пайки». Заполнение слотов шанциями называют активизацией фрейма.
С помощью фреймов можно моделировать как процедурные, так и декларативные знания. На рис. 13.2 представлен пример представления процедурных знаний.
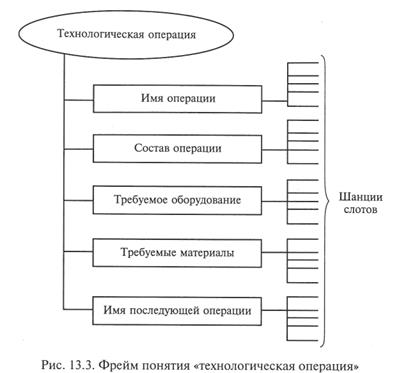
На рис. 13.3 приведен пример фрейма «технологическая операция», иллюстрирующий представление декларативных знаний для решения задачи проектирования технологического процесса.
По содержательному смыслу фрейма выделяют [21]:
· фреймы с иерархически вложенной структурой.
Фрейм-понятие — это фрейм типа И. Например, фрейм «операция» содержит объединенные связкой И имена слотов «что делать», «что это дает», «как делать», «кто делает», «где делать» и т.д., а фрейм «предмет» — слоты с именами «назначение», «форма», «вес», «цвет» и т.д.
Фрейм-меню — это фрейм типа ИЛИ. Он служит для организации процедурных знаний с помощью оператора «выбрать». Например, фрейм «что делать» может состоять из объединенных связкой ИЛИ слотов «решить уравнение», «подставить данные», «уточнить задачу» и т.д., причем каждый из этих слотов может иметь несколько значений.
Фрейм с иерархически вложенной структурой предполагает, что в нем в качестве значений слотов можно использовать имена других фреймов, слотов и т.д., т. е. использовать иерархическую структуру, в которой комбинируются другие виды фреймов (в итоге получают так называемые фреймы-сценарии).
Значения слотов могут содержать ссылки на так называемые присоединенные процедуры. Различают два вида присоединенных процедур: процедуры-демоны; процедуры-слуги.
Процедуры-демоны присоединяются к слоту и активизируются при изменении информации в этом слоте (выполняют вспомогательные операции — например, автоматически корректируют информацию во всех других структурах, где используется значение данного слота).
1. Процедура «Если — добавлено» (IF —ADDED) выполняется, когда новая информация помещается в слот.
2. Процедура «Если — удалено» (IF —REMOVED) выполняется, когда информация удаляется из слота.
3. Процедура «Если —нужно» (IF —NEEDED) выполняется, когда запрашивается информация из пустого слота.
Процедуры-слуги активизируются при выполнении некоторых условий относительно содержимого слотов (часто по запросу). Данные процедуры определяются пользователем при создании фрейма. Например, во фрейме «Учебная аудитория» можно предусмотреть слоты «Длина» и «Ширина», а по их значениям вычислять значение слота «площадь».
Фреймы позволяют использовать многие свойства знаний и достаточно широко употребляются. Их достоинства и недостатки схожи с достоинствами и недостатками семантических сетей, которые будут рассмотрены ниже.
Модель семантической сети (модель Куилиана). Семантическая сеть — это направленный граф с поименованными вершинами и дугами, причем узлы обозначают конкретные объекты, а дуги — отношения между ними [21]. Как следует из определения, данная модель представления знаний является более общей по отношению к фреймовой модели (иными словами, фреймовая модель — частный случай семантической сети). Семантическую сеть можно построить для любой предметной области и для самых разнообразных объектов и отношений.
В семантических сетях используют три типа вершин:
· вершины-понятия (обычно это существительные);
· вершины-события (обычно это глаголы);
· вершины-свойства (прилагательные, наречия, определения).
Дуги сети (семантические отношения) делят на четыре класса:
· лингвистические (падежные, глагольные, атрибутивные);
· логические (И, ИЛИ, НЕ);
· теоретико-множественные (множество — подмножество, отношения целого и части, родовидовые отношения);
· квантифицированные (определяемые кванторами общности 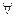
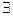
(Кванторы — это логические операторы, переводящие одну высказывательную форму в другую и позволяющие указывать объем тех значений предметных переменных, для которых данная выcказывателъная форма истинна).
Приведем два примера.
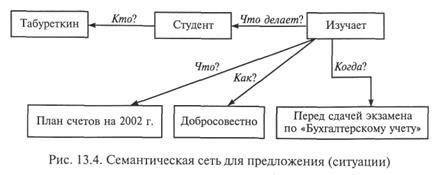
На рис. 13.4 представлена семантическая сеть для предложения (ситуации) «студент Табуреткин добросовестно изучает новый план счетов на 2002 г. перед сдачей экзамена по дисциплине «Бухгалтерский учет».
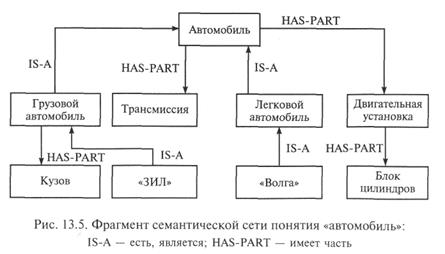
Рис. 13.5 содержит фрагмент семантической сети для понятия «автомобиль».
Из приведенных примеров понятно, почему многие специалисты по ИИ считают фрейм частным случаем семантической сети со строго структурированными знаниями.
Основное достоинство методов моделирования знаний с помощью семантических сетей и фреймов — универсальность, удобство представления как декларативных, так и процедуральных знаний. Существует и два недостатка:
· громоздкость, сложность построения и изменения;
· потребность в разнообразных процедурах обработки, связанная с разнообразием типов дуг и вершин.
Модели на основе теоретического подхода.В рамках реализации теоретического подхода применяют логические модели, прежде всего использующие представления знаний в системе логики предикатов. Преимущества такого подхода очевидны: единственность теоретического обоснования и возможность реализации системы путем введения формально точных определений и правил получения выводов. Однако в полной мере претворить в жизнь данный подход даже для «простых» задач оказалось весьма сложно. Поэтому появились попытки перейти от формальной логики к так называемой человеческой логике (модальной логике, многозначной логике и др.), модели которой в большей или меньшей степени учитывают «человеческий фактор», т.е. являются в определенном смысле компромиссными в плане использования и теоретического, и эвристического подходов.
Очень коротко остановимся на ставшей классической предикатной модели представления знаний. Первые попытки использовать такую модель относятся к 50-м гг. прошлого века. Дадим несколько определений.
Пусть имеется некоторое множество объектов, называемое предметной областью. Выражение P(x1, x2, . хn), где х1. xn — предметные переменные, а Р принимает значения 0 или 1, и называется логической функцией, или предикатом.
Предикат Р(х1, х2, . хn) задает отношение между элементами х1 х2, . хn и обозначает высказывание, что «х1, х2, . хn находятся между собой в отношении Р». Например, если А — множество целых чисел, а Р(а) — высказывание «а — положительное число», то Р(а) = 1 при а > 0 и Р(а) = 0 при а £0.
Из подобного рода элементарных высказываний с помощью логических связок образуют более сложные высказывания, которые могут принимать те же значения — «истина» и «ложь». В качестве связок используются конъюнкция, дизъюнкция, импликация, отрицание, эквивалентность.
Предикат от п переменных называют n-местным.
Одноместные (унарные) предикаты отражают свойства определенного объекта или класса объектов. Многоместные предикаты позволяют записывать отношения, которые существуют между группой элементов.
Если а — тоже предикат, то Р(а) — предикат 2-го порядка и далее до n-го порядка.
Приведем примеры различных предикатов.
1. Унарный предикат (высказывание) «река впадает в Каспийское море» имеет значение 1, если «река» = «Волга», и значение 0, если «Река» = «Днепр».
2. Двухместный предикат «x1не меньше х2» может иметь значение 1 или 0 в зависимости от значений х1и х2. Если значение предиката тождественно равно 1 при любых значениях предметных переменных, он называется тавтологией.
В аппарат исчисления предикатов входят также символы функций (обычно обозначаемые латинскими буквами f, g, h и т.д.), задаваемых на множестве предметных переменных, и кванторы общности 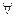
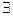
3. Представление с помощью предиката знаний, заключенных в теореме Пифагора: P
Иногда используется такая форма записи:
РАВНЫ [СУММА (КВАДРАТ(х), КВАДРАТ(y)), КВАДРАТ (z)].
Предикат Р равен 1, если х, у, z — соответственно длины катетов и гипотенузы прямоугольного треугольника.
Как уже отмечалось, предикаты удобны для описания декларативных знаний (фактов, событий и т.п.). Их главные достоинства — возможность реализации строгого вывода знаний (исчисления предикатов) и сравнительная компактность модели. К сожалению, предикаты мало пригодны для записи процедуральных знаний. Кроме того, опыт показал, что человеческое знание по своей структуре много сложнее структуры языков предикатного типа, поэтому требуются специальные навыки «подгонки» структуры реального знания под структуру модели (как правило, значительно обедняющей исходные знания).
Источник