ОПРЕДЕЛЕНИЕ КРУТИЗНЫ СКАТОВ
Наиболее распространенный способ определения крутизны скатов — по шкале заложений, помещаемой в южной части листа карты. Этот способ заключается в том, что для нахождения крутизны ската на каком-либо участке дороги с помощью полоски бумаги или циркуля измеряют расстояние между горизонталями, проходящими через те точки, крутизна ската между которыми определяется. Отмеченное на полоске бумаги или же обозначенное раствором циркуля расстояние (на рис. 20 оно обозначено утолщенной полоской) переносят на шкалу заложений.
Тогда у основания шкалы можно прочитать величину крутизны ската. Так, на нашем рисунке крутизна ската между двумя смежными горизонталями, отмеченными черточкой, оказалась равной 4°.
После определения крутизны ската по карте можно решить, учитывая возможности своих средств передвижения, условия погоды и время года, преодолим или нет данный участок местности, лежащий на маршруте движения.
Для точного определения крутизны ската существует формула
| h | ||
| tg α | = | —— |
| d |
где а — угол в градусах, обозначающий критузну ската;
h — относительное превышение точек, расположенных на скате, крутизна которого определяется;
d — расстояние между точками, снятое с карты.
В приведенной формуле величины h и d должны быть в одних и тех же единицах измерения (обычно в метрах).
Определение крутизны ската между точками А и Б по разности их абсолютных высот
Пример. Требуется определить крутизну ската по дороге между пунктами А и Б, имеющимися на карте. На рисунке положение точек А и Б карты изображено в виде проекции на вертикальную плоскость, рассекающую скат.
Решение. По горизонталям (отметкам) карты определяем абсолютные высоты точек А и Б. Пусть они соответственно равны 110 и 230 м. Расстояние между ними (АБ1 = d), измеренное по карте, оказалось равным 600 м. Превышение между точками А и Б будет равно h= 230-110=120 м. Тогда , откуда (по специальной таблице значений тангенсов углов) находим крутизну ската а = 11,5°.
Источник
Определение крутизны скатов.



Крутизна ската определяется по карте по степени сближения между собой горизонталей на этом скате, т.е. по величине заложения ската между двумя смежными горизонталями.

Шкалой заложений называется специальный график, который печатается на всех листах топографических карт рядом с линейным масштабом.
Для определения крутизны ската надо взять циркулем или с помощью полоски бумаги расстояние между двумя смежными горизонталями на интересующем нас скате и приложив этот отрезок к шкале заложений найти место точного совпадения раствора циркуля с одним из перпендикуляров графика. Значение угла наклона ската определяют цифрой, подписанной против соответствующего перпендикуляра.
Если горизонтали на скате расположены очень близко одна к другой, и взять циркулем расстояние между ними затруднительно, тогда удобнее пользоваться правой частью шкалы, беря при этом по карте заложения между соседними утолщенными горизонталями.

По карте обычно не приходится определять крутизну скатов более 25°. Для углов не превышающих эту величину, можно приближенно считать, что крутизна ската a обратно пропорциональна заложению d и прямо пропорциональна высоте сечения h:

На этом и основан глазомерный способ определения крутизны ската по карте. Чтобы применять этот способ, надо предварительно определить по шкале заложений крутизну ската, которая на данном листе карты соответствует заложению в 1 см.
Дальнейшая задача по определению крутизны ската сводится в основном к глазомерной оценке в сантиметрах заложения между смежными горизонталями данного ската. Определяемая крутизна получается как частное от деления крутизны ската, соответствующего заложению в 1 см, на величину заложения.
Например, если на карте масштаба 1:25 000 с высотой основного сечения 10 м определить по шкале заложений крутизну ската при заложении в 1 см, то она будет равна примерно 2,5°. Поэтому, если на данном листе карты заложение между смежными горизонталями равно 0,5 см, то крутизна в этом месте будет около 5°, а если заложение равно 1мм, то крутизна будет около 25°.
Крутизна ската, соответствующая заложению в 1 см, зависит от масштаба карты, а также от высоты сечения и неодинакова на различных картах. Однако, на всех листах карт с нормальной высотой сечения (т.е. с высотой сечения, равной 0,02 величины масштаба карты) заложению в 1 см соответствует одна и та же крутизна, равная 1,2° или округленно 1°.
Поэтому для указанных карт применимо общее приближенное правило, определяемая крутизна ската во столько раз больше (меньше) 1°, во сколько раз его заложение между смежными сплошными горизонталями меньше (больше) 1 см.
Источник
Определение по карте крутизны скатов



Рельеф на топографических картах изображается кривыми замкнутыми линиями, соединяющими точки местности с одинаковыми абсолютными высотами, которые называются горизонталями.
Направления понижения скатов определяются:
— по указателям скатов на горизонталях (бергштрихам), которые своими свободными концами направлены в сторону понижения ската;
— по подписи отметок горизонталей (верх цифры смотрит в сторону повышения высот, низ — понижения);
— по водоемам, т.е. высоты всегда понижаются к элементам гидрографии.
Крутизна ската представляет собой угол, образованный наклонной поверхностью ската и горизонтальной плоскостью. Она обычно измеряется в градусах и является основным показателем проходимости техники и допустимой скорости движения. Так, скаты крутизной до 20° могут преодолеваться колесной техникой, до 30° – гусеничной, свыше 30° – практически недоступны для колесных и гусеничных машин.
Крутизна ската на карте определяется по расстоянию между двумя сплошными соседними горизонталями, называемым заложением. Чем ближе друг к другу на карте расположены горизонтали, тем скат круче; чем больше расстояние между двумя соседними горизонталями, тем скат более пологий. Свойство горизонталей передавать крутизну ската позволяет изобразить на карте его форму.
По форме скаты могут быть ровные, вогнутые, выпуклые и волнистые. Условия наблюдения и ведения огня наиболее благоприятны на ровных и вогнутых скатах, неблагоприятные – на выпуклых и волнистых.
На топографических картах 1:25 000, 1:50 000 и 1:100 000 основная высота сечения рельефа подобрана таким образом, что заложению между основными горизонталями в 1 см соответствует крутизна ската 1,2°. Отсюда следует, что заложению в 1 мм соответствует крутизна ската 12°, заложению в 2 мм – 6° (округленно 5°), заложению в 5 мм – 2,4° (округленно 2°) и т.д.
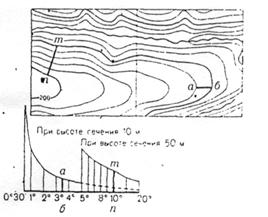
Более точно крутизна ската определяется с помощью специального графика, который называется шкалой заложений и помещается в легенде карты. В основании шкалы подписаны цифры, обозначающие крутизну скатов в градусах. На перпендикулярах к основанию отложены соответствующие им заложения. Шкала заложений дается для двух высот сечений: одна — для заложений между основными горизонталями, другая — для заложений между утолщенными горизонталями (рис.8.37).
Для определения крутизны ската измеряют расстояние между двумя сплошными соседними горизонталями в нужном направлении и откладывают его так, как показано на рисунке.
Рис. 8. 37. Определение крутизны скатов по шкале заложений
Отсчет внизу по шкале против отложенного отрезка укажет крутизну ската в градусах. На крутых скатах, особенно в горной местности, где горизонтали располагаются близко одна от другой, крутизну ската удобнее определять по утолщенным горизонталям. Крутизну ската определяют в таком случае по правой части шкалы. В указанных примерах отрезку аб соответствует крутизна ската 3,5°, а пт – 10°.
Источник
Вопрос 2: Определение крутизны скатов
Крутизна ската определяется по шкале заложений или глазомерно. Для определения крутизны ската по шкале заложений необходимо отмерить циркулем, линейкой или полоской бумаги отрезок между двумя смежными основными или утолщенными горизонталями, приложить его к шкале и прочитать число градусов у основания шкалы. Крутизну ската между смежными утолщенными горизонталями определяют по шкале, соответствующей пятикратному сечению.
При глазомерном определении крутизны ската оценивают в миллиметрах заложение Д (промежуток между основными горизонталями) и определяют крутизну (в градусах) по формуле 
Этот способ применим при высоте сечения рельефа на картах масштаба 1:25 000 — 5м; 1:50 000 — 10 м; 1:100000—20 м; 1:200000 — 40 м
Наиболее точно крутизну ската можно определить по формуле
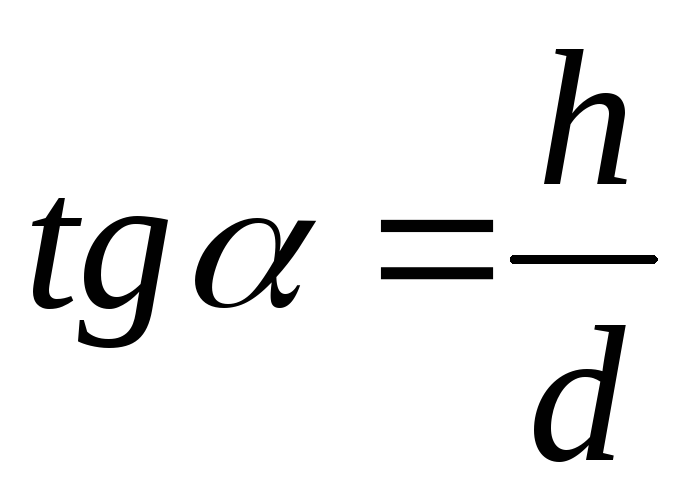
где: h — высота сечения рельефа, м;
d — расстояние между двумя смежными горизонталями, м.
Мерой крутизны может также служить уклон i, выраженный в процентах (%) или в промилле ( 0 /00 — тысячных долях) заложения.
Вычисления ведут в первом случае по формуле: — 
а во втором случае по формуле: — 
где h соответствует превышению на расстояние d.
Вопрос 3: Измерение расстояний по карте
Масштаб карты — степень уменьшения линяй на карте относительно соответствующих им линий на местности (точнее их горизонтальных проложений). При измерении расстоянии по карте пользуются численным, линейным или поперечным масштабом.
1:50000
в 1 сантиметре 500 метров
м. 1000 500 0 1 2 км
Рис. 2. Численный и линейный масштабы, помещаемые на карте
Численный масштаб (рис. 2) — масштаб карты, выраженный дробью, числитель которой — единица, а знаменатель — число, показывающее, во сколько раз уменьшены на карте линии местности. Чем меньше знаменатель масштаба, тем крупнее масштаб карты. Ниже численного масштаба на картах указывается величина масштаба — расстояние на местности (в метрах или километрах), соответствующее одному сантиметру карты (величина масштаба в метрах равна знаменателю численного масштаба без двух последних нулей).
При определении расстояния с помощью численного масштаба линия на карте измеряется линейкой, и полученный результат в сантиметрах умножается на величину масштаба.
Линейный масштаб — графическое выражение численного масштаба, представляет собой шкалу, на которой деления соответствуют определенным расстояниям на местности. По линейному масштабу можно измерять или откладывать на карте расстояния с помощью циркуля-измерителя или линейки. На рис. 2 отложенное расстояние равно 1650 м
Вставить рисунок №3(12)!
Поперечный масштаб—график (обычно на металлической пластинке) для измерения и откладывания расстояний на карте с предельной графической точностью (0,1 мм)
Стандартный (нормальный) поперечный масштаб (рис.3) имеет большие деления, равные 2 см, малые деления (слева от нуля), равные 2 мм, и отрезки между вертикальной и наклонной линиями, равные по первой горизонтальной линии 0,2 мм, по второй— 0,4 мм, по третьей—0,6 мм и т.д. С помощью стандартного поперечного масштаба можно измерять и откладывать расстояния на карте любого (метрического) масштаба Отсчет расстояния по поперечному масштабу состоит из суммы отсчета на основании графика и отсчета отрезка между нулевой вертикальной и наклонной линиями На рис 12 расстояние между точками А и В при масштабе карты 1 :50 000 равно 2750 м (2 км+700 м+50 м), а при масштабе 1:100000 — 5500 м (4 км+1400 м+100 м).
Измерение расстояний циркулем-измерителем. При измерении расстояния по прямой линии иглы циркуля измерителя устанавливают на начальную и конечную точки, затем, не изменяя раствора циркуля измерителя, по линейному или поперечному масштабу отсчитывают расстояние. В том случае, когда раствор циркуля-измерителя превышает длину линейного или поперечного масштаба, целое число километров определяют по квадратам координатной сетки, а остаток — обычным порядком по масштабу.
Ломаные линии удобно измерять путем последовательного наращивания раствора циркуля-измерителя прямолинейными отрезками, как показано на рис 13,а.
Расстояния по извилистым линиям измеряют последовательным отложением шага циркуля измерителя (рис 13,6). Величина шага зависит от степени извилистости линий, но, как правило, берется равной 1 см. Для исключения систематической ошибки длину шага циркуля измерителя, определенную по масштабу или линейке, следует проверять измерением линии километровой сетки длиной 6-8 см.
Измерение расстояний курвиметром. Вращением колесика стрелку курвиметра устанавливают на нулевое деление, а затем прокатывают колесико по измеряемой линии слева направо или Снизу вверх; полученный отсчет в сантиметрах умножают на величину масштаба данной карты.
Поправки в расстояния, измеренные по извилистым линиям (по дорогам). Длина (протяженность) маршрута, измеренная по карте, всегда несколько меньше ее действительной длины, так как на карте невозможно изобразить все извилины и повороты дорог. Кроме того, на карте измеряется не кривая линия, а хорды отдельных участков этой кривой. Увеличение протяженности маршрута за счет неровностей местности незначительное коэффициент увеличения при угле наклона 12° составляет 1,02.
В табл.2 приведены коэффициенты увеличения протяженности маршрута, измеренного по карте.
Источник