Научная электронная библиотека
Оразбаев Б. Б., Курмангазиева Л. Т., Коданова Ш. К.,
3.4. Методы моделирования систем
1. Общие подходы к моделированию систем.
2. Аналитические и статистические методы.
3. Математическая логика.
4. Лингвистические и семиотические представления.
5. Графические методы.
6. Методы, направленные на активизацию использования интуиции и опыта специалистов.
1. Общие подходы к моделированию систем
Постановка любой задачи заключается в том, чтобы перевести её словесное, вербальное описание в формальное. В случае относительно простых задач такой переход осуществляется в сознании человека, который не всегда даже может объяснить, как он это сделал. Если полученная формальная модель (математическая зависимость между величинами в виде формулы, уравнения, системы уравнений) опирается на фундаментальный закон или подтверждается экспериментом, то этим доказывается её адекватность отображаемой ситуации, и модель рекомендуется для решения задач соответствующего класса.
По мере усложнения задач получение модели и доказательство её адекватности усложняется. Вначале эксперимент становится дорогим и опасным (например, при создании сложных технических комплексов, при реализации космических программ и т.д.), а применительно к экономическим объектам эксперимент становится практическим нереализуемым, задача переходит в класс проблем принятия решений, и постановка задачи, формирование модели, т.е. перевод вербального описания в формальное, становится важной составной частью процесса принятия решения.
Перевод вербального описания в формальное, осмысление, интерпретация модели и получаемых результатов становятся неотъемлемой частью практически каждого этапа моделирования сложной развивающейся системы.
Для решения проблемы перевода вербального описания в формальное описание в различных областях деятельности стали развиваться специальные приёмы и методы. Так, возникли методы типа «мозговой атаки», «сценариев», экспертных оценок, «дерева целей» и т.п.
В свою очередь, развитие математики шло по пути расширения средств постановки и решения трудноформализуемых задач. Наряду с детерминированными, аналитическими методами классической математики возникла теория вероятностей и математическая статистика (как средство доказательства адекватности модели на основе представительной выборки и понятия вероятности правомерности использования модели и результатов моделирования). Для задач с большей степенью неопределённости инженеры стали привлекать теорию множеств, математическую логику, математическую лингвистику, теорию графов, теорию нечетких множеств, что во многом стимулировало развитие этих направлений. Иными словами, математика стала постепенно накапливать средства работы с неопределённостью, со смыслом, который классическая математика исключала из объектов своего рассмотрения.
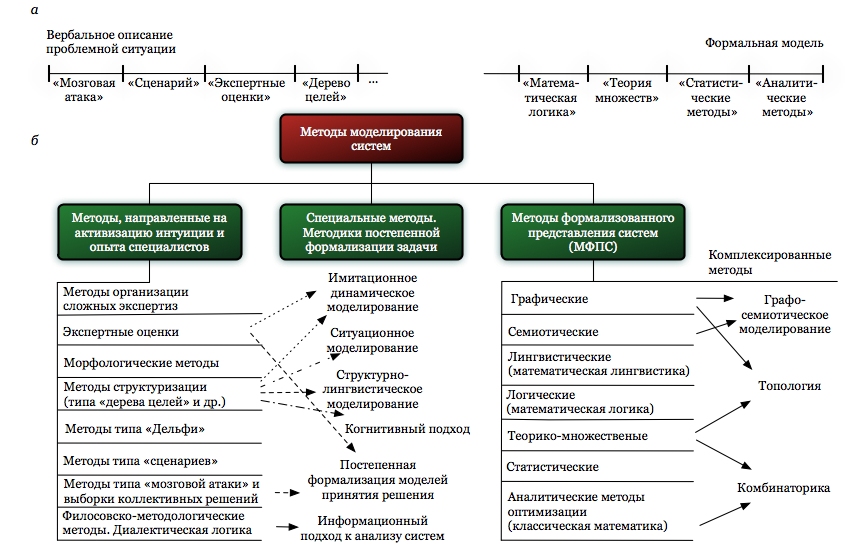
Таким образом, между неформальным, образным мышлением человека и формальными моделями классической математики сложился как бы «спектр» методов, которые помогают получать и уточнять (формализовать) вербальное описание проблемной ситуации, с одной стороны, и интерпретировать формальные модели, связывать их с реальной действительностью, с другой. Этот спектр условно представлен на рис. 3.4, а.
Рис. 3.4. Модели и моделирование систем
Развитие методов моделирования, разумеется, шло не так последовательно, как показано на рис. 3.4, а. Методы возникали и развивались параллельно. Существуют различные модификации сходных методов. Их по-разному объединяли в группы, т.е. исследователи предлагали разные классификации (в основном – для формальных методов). Постоянно возникают новые методы моделирования как бы на «пересечении» уже сложившихся групп. Однако основную идею – существование «спектра» методов между вербальным и формальным представлением проблемной ситуации – рис. 3.4, а иллюстрирует.
Первоначально исследователи, развивающие теорию систем, предлагали классификации систем и старались поставить им в соответствие определённые методы моделирования, позволяющие наилучшим образом отразить особенности того или иного класса. Такой подход к выбору методов моделирования подобен подходу прикладной математики.
Однако в отличие от последней, в основу которой положены классы прикладных задач, системный анализ может один и тот же объект или одну и ту же проблемную ситуацию (отображать разными классами систем и соответственно различными моделями, организуя таким образом как бы процесс постепенной формализации задачи, т.е. «выращивание» её формальной модели. Подход помогает понять, что неверно выбранный метод моделирования может привести к неверным результатам, к невозможности доказательства адекватности модели, к увеличению числа итераций и затягиванию решения проблемы.
2. Аналитические и статистические методы
Аналитические и статистические методы получили наибольшее распространение в практике проектирования и управления. Для представления промежуточных и окончательных результатов моделирования широко используются графические представления (графики, диаграммы и т.п.). Однако последние являются вспомогательными; основу же модели, доказательства её адекватности составляют те или иные направления аналитических и статистических представлений. Поэтому, несмотря на то, что по основным направлениям этих двух классов методов в вузах читаются самостоятельные курсы лекций, мы всё же кратко охарактеризуем их особенности, достоинства и недостатки с точки зрения возможности использования при моделировании систем.
Аналитическими в рассматриваемой классификации названы методы, которые отображают реальные объекты и процессы в виде точек (безразмерных в строгих математических доказательствах), совершающих какие-либо перемещения в пространстве или взаимодействующих между собой.
Основу понятийного (терминологического) аппарата этих представлений составляют понятия классической математики (величина, формула, функция, уравнение, система уравнений, логарифм, дифференциал, интеграл и т.д.).
Аналитические представления имеют многовековую историю развития, и для них характерно не только стремление к строгости терминологии, но и к закреплению за некоторыми специальными величинами определённых букв (например, удвоенное отношение площади круга к площади вписанного в него квадрата π ≈ 3,14; основание натурального логарифма – е ≈ 2,7 и т.д.).
На базе аналитических представлений возникли и развиваются математические теории различной сложности – от аппарата классического математического анализа (методов исследования функций, их вида, способов представления, поиска экстремумов функций и т.п.) до таких новых разделов современной науки – исследования операции, системный анализ, как математическое программирование (линейное, нелинейное, динамическое и т.п.), теория игр (матричные игры с чистыми стратегиями, дифференциальные игры и т.п.).
Эти теоретические направления стали основой многих прикладных, в том числе теории автоматического управления, теории оптимальных решений и т.д.
При моделировании систем применяется широкий спектр символических представлений, использующих «язык» классической математики. Однако далеко не всегда эти символические представления адекватно отражают реальные сложные процессы, и их в этих случаях, вообще говоря, нельзя считать строгими математическими моделями.
Большинство из направлений математики не содержат средств постановки задачи и доказательства адекватности модели. Последняя доказывается экспериментом, который по мере усложнения проблем становится также всё более сложным, дорогостоящим, не всегда бесспорен и реализуем.
В то же время в состав этого класса методов входит относительно новое направление математическое программирование, которое содержит средства постановки задачи и расширяет возможности доказательства адекватности моделей (стохастическое, нечеткое программирование).
Статистические представления сформировались как самостоятельное научное направление в середине прошлого века (хотя возникли значительно раньше). Основу их составляет отображение явлений и процессов с помощью случайных (стохастических) событий и их поведений, которые описываются соответствующими вероятностными (статистическими) характеристиками и статистическими закономерностями.
Статистические отображения системы в общем случае (по аналогии с аналитическими) можно представить как бы в виде «размытой» точки (размытой области) в n-мерном пространстве, в которую переводит систему (её учитываемые в модели свойства) оператор Ф[Sx]. «Размытую» точку следует понимать как некоторую область, характеризующую движение системы (её поведение); при этом границы области заданы с некоторой вероятностью p («размыты») и движение точки описывается некоторой случайной функцией.
Закрепляя все параметры этой области, кроме одного, можно получить срез по линии а–b, смысл которого – воздействие данного параметра на поведение системы, что можно описать статистическим распределением по этому параметру. Аналогично можно получить двумерную, трёхмерную и т.д. картины статистического распределения.
Статистические закономерности можно представить в виде дискретных случайных величин и их вероятностей, или в виде непрерывных зависимостей распределения событий, процессов.
Для дискретных событий соотношение между возможными значениями случайной величины xi и их вероятностями pi, называют законом распределения и либо записывают в виде ряда (табл. 3.1), либо представляют в виде зависимостей F(x) (рис. 3.5, а) или p(х) (рис. 3.5, в).
Для непрерывных случайных величин (процессов) закон распределения представляют (соответственно дискретным законам) либо в виде функции распределения (интегральный закон распределения – рис. 3.5, б), либо в виде плотности вероятностей (дифференциальный закон распределения – рис. 3.5, г). В этом случае 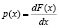
Для полной группы несовместных событий имеют место условия нормирования:
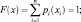
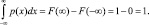
Часто применяют тот или иной вид зависимостей, приведенных на рис. 3.5, более подходящий для соответствующих приложений.
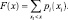
Источник
MT1400: Общая теория систем
Постановка любой задачи заключается в том, чтобы перевести ее вербальное (словесное) описание в формальное.
В случае относительно простых задач такой переход осуществляется в сознании человека, который не всегда даже может объяснить, как он это сделал. Если полученная формальная модель (математическая зависимость между величинами в виде формулы, уравнения, системы уравнений) опирается на фундаментальный закон или подтверждается экспериментом, то этим доказывается ее адекватность отображаемой ситуации, и модель рекомендуется для решения задач соответствующего класса.
По мере усложнения задач получение модели и доказательство ее адекватности усложняется. Вначале эксперимент становится дорогостоящим и опасным (например, при создании сложных технических комплексов, реализации космических программ и т.д.), а применительно к экономическим объектам — практически нереализуемым. Тогда задача переходит в класс проблем принятия решений, и постановка задачи, формирование модели, т.е. перевод вербального описания в формальное, становятся важной составной частью процесса принятия решения. Причем эту составную часть не всегда можно выделить как отдельный этап, завершив который, можно обращаться с полученной формальной моделью так же, как с обычным математическим описанием; строгим и абсолютно справедливым. Большинство реальных ситуаций проектирования сложных технических комплексов и управления экономикой необходимо отображать классом самоорганизующихся систем, модели которых должны постоянно корректироваться и развиваться. При этом возможно изменение не только модели, но и метода моделирования, что часто является средством развития представления ЛПР о моделируемой ситуации.
Иными словами, перевод вербального описания задачи или проблемной ситуации в формальное, осмысление, интерпретация модели и получаемых результатов становятся неотъемлемой частью практически каждого этапа моделирования сложной развивающейся системы. Чтобы точнее охарактеризовать такой подход к моделированию процессов принятия решений, говорят о создании как бы «механизма» моделирования, «механизма» принятия решений (например, «хозяйственный механизм», «механизм проектирования и развития предприятия» и т.п.).
Возникающие у исследователей вопросы: «Как формировать такие развивающиеся модели или «механизмы»? Как доказывать адекватность моделей?» — и являются основным предметом системного анализа.
Для решения проблемы перевода вербального описания или проблемной ситуации в формальное отображение в различных областях деятельности стали развиваться специальные приемы и методы. Так возникли методы «мозговой атаки», «сценариев», экспертных оценок, «дерева целей» и т.п.
В свою очередь развитие математики шло по пути расширения средств постановки и решения трудно формализуемых задач.
Наряду с детерминированными, аналитическими методами классической математики возникла теория вероятностей и математическая статистика (как средство доказательства адекватности модели на основе представительной выборки и понятия вероятности правомерности использования модели и результатов моделирования). Для задач с большей степенью неопределенности инженеры стали привлекать теорию множеств, математическую логику, математическую лингвистику, теорию графов, что во многом стимулировало развитие этих направлений. Иными словами, математика стала постепенно накапливать средства работы с неопределенностью, со смыслом, который классическая математика исключала из объектов своего рассмотрения.
Таким образом, между неформальным, образным мышлением человека и формальными моделями классической математики сложился «спектр» методов, которые помогают получать и уточнять (формализовать) вербальное описание проблемной ситуации, с одной стороны, и интерпретировать формальные модели, связывать их с реальной действительностью, с другой. Этот «спектр» методов условно представлен на рис. 2.3, а.
Развитие методов моделирования, разумеется, шло не так последовательно, как показано на рис. 2.3, а. Методы возникали и развивались параллельно. Существуют различные модификации сходных методов их по-разному объединяли в группы, т.е. исследователи предлагали разные классификации. Постоянно возникают новые методы моделирования как бы на «пересечении» уже сложившихся групп. Однако основную идею существование «спектра» методов между вербальным и формальным представлением проблемной ситуации — этот рисунок иллюстрирует.
Первоначально исследователи, развивающие теорию систем, предлагали классификации систем, старались поставить им в соответствие определенные методы моделирования, позволяющие наилучшим образом отразить особенности того или иного класса. Такой подход к выбору методов моделирования подобен подходу прикладной математики. Однако в отличие от последней, в основу которой положены классы прикладных задач, системный анализ может один и тот же объект или одну и ту же проблемную ситуацию (в зависимости от степени неопределенности и по мере их познания) отображать разными классами систем и, соответственно, различными моделями.
Существует и другая точка зрения. Если последовательно менять методы приведенного на рис. 2.3, а «спектра» (не обязательно используя все), то можно постепенно, ограничивая полноту описания проблемной ситуации (что неизбежно при формализации), но сохраняя наиболее существенные с точки зрения цели (структуры целей) компоненты и связи между ними, перейти к формальной модели.
Такая идея реализовалась, например, при создании программного обеспечения ЭВМ и автоматизированных информационных систем путем последовательное перевода описания задачи с естественного языка на язык высокого уровня (язык управления заданиями, информационно-поисковый язык, язык моделирования, автоматизации проектирования), а с него — на один из языков программирования, подходящий для данной задачи (ПЛ/1, ПАСКАЛЬ, ЛИСП, СИ, ПРОЛОГ и т.п.), который в свою очередь транслируется в коды машинных команд, приводящих в действие аппаратную часть ЭВМ.
В то же время анализ процессов изобретательской деятельности, опыта формирования сложных моделей принятия решений показал, что практика не подчиняется такой логике, т.е. человек поступает иначе: он попеременно выбирает методы из левой и правой частей «спектра», приведенного на рис. 2.3, а.
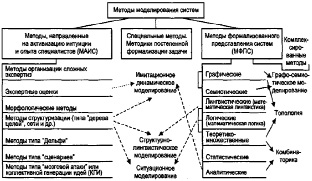
Поэтому удобно «переломить» этот «спектр» методов примерно в середине, где графические методы смыкаются с методами структуризации, т.е. разделить методы моделирования систем на два больших класса: методы формализованного представления систем и методы, направленные на активизацию использования интуиции и опыта специалистов. Возможные классификации этих двух групп методов приведены на рис. 2.3, б.
МАИС и МФПС показаны на рисунке сплошной и различными штриховыми линиями.
Отметим, что на рис. 2.3, б в группе МАИС методы расположены снизу вверх примерно в порядке возрастания возможностей формализации, а в группе МФПС — снизу вверх возрастает внимание к содержательному анализу проблемы и появляется все больше средств такого анализа. Такое упорядочение помогает сравнивать методы и выбирать их при формировании развивающихся моделей принятия решений, при разработке методик системного анализа.
Классификации МАИС и особенно МФПС могут быть разными. На рис. 2.3, б приведена классификация МФПС, предложенная Ф. Е. Темниковым и подробнее рассматриваемая в параграфе 2.4, в которой приведены и другие примеры классификаций МФПС.
Специалист по системному анализу должен понимать, что любая классификация условна. Она — лишь средство, помогающее ориентироваться в огромном числе разнообразных методов и моделей. Поэтому разрабатывать классификацию нужно обязательно с учетом конкретных условий, особенностей моделируемых систем (процессов принятия решений) и предпочтений ЛПР, которым можно предложить выбрать классификацию.
Новые методы моделирования часто создаются на основе сочетания ранее существовавших классов методов.
Так, методы, названные на рис. 2.3 комплексированными (комбинаторика, топология), начинали развиваться параллельно в рамках линейной алгебры, теории множеств, теории графов, а затем оформились в самостоятельные направления.
Существуют также новые методы, базирующиеся на сочетании средств МАИС и МФПС. Эта группа методов представлена на рис. 2.3, б в качестве самостоятельной группы методов моделирования, обобщенно названной специальными методами. Стрелками показано, какие средства МАИС и МФПС использованы при создании этих методов.
Наибольшее распространение получили следующие специальные методы моделирования систем:
- имитационное динамическое моделирование (System Dynamics Symulation Modeling);
в этом методе используется удобный для человека структурный язык, помогающий выражать реальные взаимосвязи, отображающие в системе замкнутые контуры управления, и аналитические представления, позволяющие реализовать формальное исследование полученных моделей на ЭВМ с использованием специализированного языка DYNAMO;
это направление базируется на отображении в памяти ЭВМ и анализе проблемных ситуаций с применением специализированного языка, разрабатываемого с помощью выразительных средств теории множеств, математической логики и теории языков;
подход основан на использовании для реализации идей комбинаторики структурных представлений разного рода, с одной стороны, и средств математической лингвистики, с другой; в расширенном понимании подхода в качестве языковых (лингвистических) средств используются и другие методы дискретной математики (языки, основанные на теоретико-множественных представлениях, на использовании средств математической логики, семиотики);
- когнитивный подход (от лат. cognitio — знание, познание);
подход базируется на идеях когнитивной психологии;
- подход, базирующийся на идее постепенной формализации моделей принятия решений путем поочередного использования средств МАИС и МФПС;
этот подход к моделированию самоорганизующихся (развивающихся) систем стал основой практически всех методик системного анализа;
- теория информационного поля и информационных цепей (информационный подход к моделированию и анализу систем);
теория основана на использовании для активизации интуиции ЛПР законов диалектики, а в качестве средства формализованного отображения объекта или проблемной ситуации — аппарата математической теории поля и теории цепей; для краткости подход назван информационным, поскольку в его основе лежит отображение реальных ситуаций с помощью информационных моделей.
Источник