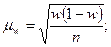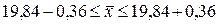Ошибка выборки способы определения

Ошибки выборки

Поможем написать любую работу на аналогичную тему

Чтобы оценить степень точности выборочного наблюдения, необходимо оценить величину ошибок, которые могут возникнуть в процессе проведения выборочного наблюдения.

Основное внимание уделяется случайным ошибкам репрезентативности.

Статистическое исследование может осуществляться по данным несплошного наблюдения, основная цель которого состоит в получении характеристик изучаемой совокупности по обследованной ее части. Одним из наиболее распространенных в статистике методов, применяющих несплошное наблюдение, является выборочный метод.

Под выборочным понимается метод статистического исследования, при котором обобщающие показатели изучаемой совокупности устанавливаются по некоторой ее части на основе положений случайного отбора. При выборочном методе обследованию подвергается сравнительно небольшая часть всей изучаемой совокупности (обычно до 5 — 10%, реже до 15 — 25%). При этом подлежащая изучению статистическая совокупность, из которой производится отбор части единиц, называется генеральной совокупностью. Отобранная из генеральной совокупности некоторая часть единиц, подвергающаяся обследованию, называется выборочной совокупностью или просто выборкой.

Значение выборочного метода состоит в том, что при минимальной численности обследуемых единиц проведение исследования осуществляется в более короткие сроки и с минимальными затратами труда и средств. Это повышает оперативность статистической информации, уменьшает ошибки регистрации.

В проведении ряда исследований выборочный метод является единственно возможным, например, при контроле качества продукции (товара), если проверка сопровождается уничтожением или разложением на составные части обследуемых образцов (определение сахаристости фруктов, клейковины печеного хлеба, установление носкости обуви, прочности тканей на разрыв и т.д.).

Проведение исследования социально — экономических явлений выборочным методом складывается из ряда последовательных этапов:

1) обоснование (в соответствии с задачами исследования) целесообразности применения выборочного метода;

2) составление программы проведения статистического исследования выборочным методом;

3) решение организационных вопросов сбора и обработки исходной информации;

4) установление доли выборки, т.е. части подлежащих обследованию единиц генеральной совокупности;

5) обоснование способов формирования выборочной совокупности;

6) осуществление отбора единиц из генеральной совокупности для их обследования;

7) фиксация в отобранных единицах (пробах) изучаемых признаков;

8) статистическая обработка полученной в выборке информации с определением обобщающих характеристик изучаемых признаков;

9) определение количественной оценки ошибки выборки;

10) распространение обобщающих выборочных характеристик на генеральную совокупность.

В генеральной совокупности доля единиц, обладающих изучаемым признаком, называется генеральной долей (обозначается р), а средняя величина изучаемого варьирующего признака — генеральной средней (обозначается ).

В выборочной совокупности долю изучаемого признака называют выборочной долей, или частостью (обозначается ), а среднюю величину в выборке — выборочной средней (обозначается ).

При контрольной проверке качества хлебобулочных изделий проведено 5%-ное выборочное обследование партии нарезных батонов из муки высшего сорта. При этом из 100 отобранных в выборку батонов 90 шт. соответствовали требованиям стандарта. Средний вес одного батона в выборке составлял 500,5 г при среднем квадратическом отклонении г.

На основе полученных в выборке данных нужно установить возможные значения доли стандартных изделий и среднего веса одного изделия во всей партии.

Прежде всего устанавливаются характеристики выборочной совокупности. Выборочная доля, или частость, определяется из отношения единиц, обладающих изучаемым признаком m, к общей численности единиц выборочной совокупности n:

Поскольку из 100 изделий, попавших в выборку n, 90 ед. оказались стандартными m, то показатель частости равен: = 90:100=0,9.

Средний вес изделия в выборке х = 500,5 г определен взвешиванием. Но полученные показатели частости (0,9) и средней величины (500,5 г) характеризуют долю стандартной продукции и средний вес одного изделия лишь в выборке. Дляопределения соответствующих показателей для всей партии товара надо установить возможные при этом значения ошибки выборки.

Ошибка выборки — это объективно возникающее расхождение между характеристиками выборки и генеральной совокупности. Она зависит от ряда факторов: степени вариации изучаемого признака, численности выборки, методом отбора единиц в выборочную совокупность, принятого уровня достоверности результата исследования.

Определение ошибки выборочной средней.

При случайном повторном отборе средняя ошибка выборочной средней рассчитывается по формуле:

где — средняя ошибка выборочной средней;

— дисперсия выборочной совокупности;

n — численность выборки.

При бесповторном отборе она рассчитывается по формуле:

где N — численность генеральной совокупности.

Определение ошибки выборочной доли.

При повторном отборе средняя ошибка выборочной доли рассчитывается по формуле:

где — выборочная доля единиц, обладающих изучаемым признаком;

— число единиц, обладающих изучаемым признаком;

— численность выборки.

При бесповторном способе отбора средняя ошибка выборочной доли определяется по формулам:

Предельная ошибка выборки связана со средней ошибкой выборки отношением:

При этом t как коэффициент кратности средней ошибки выборки зависит от значения вероятности Р, с которой гарантируется величина предельной ошибки выборки.

Предельная ошибка выборки при бесповторном отборе определяется по следующим формулам:

Предельная ошибка выборки при повторном отборе определяется по формуле:

Источник

Методы оценки ошибки выборки

При проведении выборочного наблюдения нельзя даже теоретически получить абсолютно точные данные, как при сплошном исследовании. Обусловлено это тем, что наблюдению подвергается не вся совокупность, а только её часть, поэтому при проведении выборочного наблюдения неизбежна некоторая свойственная ему погрешность (ошибки).

Ошибкой статистического наблюдения считается величина отклонения между расчётным и фактическим значениями признаков изучаемых объектов.

Ошибка выборки— это объективно возникающее расхождение между характеристиками выборки и генеральной совокупности. Она зависит от ряда факторов: степени вариации изучаемого признака, численности выборки, метода отбора единиц в выборочную совокупность, принятого уровня достоверности результата исследования. Чем больше величина этой ошибки, тем больше показатели выборочного наблюдения отличаются от показателей генеральной совокупности.

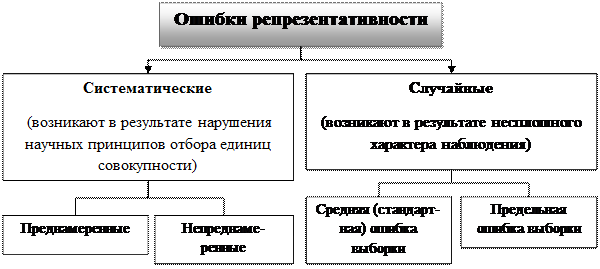
Общая величина ошибки выборочного наблюдения складывается из ошибки регистрации и ошибки репрезентативности.

Ошибка регистрации возникает при неправильном установлении факта в процессе наблюдения. Они свойственны как сплошному наблюдению, так и выборочному, но в выборочном их меньше.

Ошибка репрезентативности присуща только несплошным наблюдениям и представляет собой расхождение между выборочной характеристикой и характеристикой генеральной совокупности. Она обусловлена тем, что наблюдению подвергается не вся совокупность, а лишь её часть, и отобранные единицы не вполне отражают вариацию единиц генеральной совокупности. Величина ошибки выборки характеризует степень надёжности результатов выборки, и её необходимо учитывать при оценке параметров генеральной совокупности.

Ошибки репрезентативности бывают систематическими и случайными. Систематические ошибки могут возникать в связи с особенностями принятой системы отбора и обработки данных наблюдений или в связи с нарушением установленных правил отбора (отбираются либо заведомо лучшие, либо худшие единицы совокупности). В этом случае ошибка приобретает преднамеренный (тенденциозный) характер, и наблюдение теряет свой смысл. Общее правило отбора гласит, что у отдельных единиц генеральной совокупности должны быть совершенно одинаковые условия и возможности попасть в число единиц, входящих в выборку. Это характеризует независимость результата выборки от воли наблюдателя. Воля же наблюдателя порождает тенденциозные ошибки.

Ошибка выборки при случайном отборе носит случайный характер. Она характеризует размеры отклонений генеральных характеристик от выборочных. Возникновение случайных ошибок репрезентативности объясняется недостаточно верным представлением в выборочной совокупности различных категорий единиц генеральной совокупности, в силу чего распределение отобранной совокупности единиц не вполне точно воспроизводит распределение единиц генеральной совокупности.

Величина случайной ошибки репрезентативности выборки зависит от следующих условий:

1) принятый способ формирования выборочной совокупности (бесповторный отбор даёт меньшую ошибку);

2) объём выборки;

3) от степени варьирования изучаемого признака в генеральной совокупности.

Теоретическим обоснованием появления случайных ошибок выборки является теория вероятностей и её предельные теоремы. Сущность предельных теорем состоит в том, что в массовых явлениях совокупное влияние случайных причин на формирование закономерностей и обобщающих характеристик будет сколь угодно малой величиной или практически не зависит от случая.

Так как случайная ошибка выборки возникает в результате случайных различий между границами выборочной и генеральной совокупностей, при достаточно большом объёме выборки эта ошибка будет сколь угодно мала. Этот вывод, опирающийся на доказательстве предельных теорем, позволяет предполагать, что характеристики выборочного наблюдения могут достаточно хорошо представлять характеристики генеральной совокупности.

Случайные ошибки могут быть доведены до незначительных размеров, а главное, их размеры и пределы можно определить с достаточной точностью на основании закона больших чисел.

Случайная ошибка репрезентативности выборки разделяется на среднюю и предельную.

Средняя (стандартная) ошибка выборки – такое расхождение между средними выборочной и генеральной совокупности, которое не превышает среднего квадратического отклонения ±s.

В математической статистике доказывается, что значения средней ошибки простой случайной выборки определяются по следующим формулам:

а) для повторного отбора:

б) для бесповторного отбора:

где – средняя ошибка выборочной средней;

– дисперсия выборочной совокупности;

– среднее квадратическое отклонение в выборке;

n — численность выборки;

N — численность генеральной совокупности.

Дисперсия генеральной совокупности связана с выборочной дисперсией по формуле:

Для больших выборок (n>30) поправка на объём выборки необязательна, и можно считать генеральную и выборочную дисперсию тождественными, а значит, и величины их средних ошибок.

Средняя ошибка выборочной доли простой случайной выборки :

а) для повторного отбора:

б) для бесповторного отбора:

где – выборочная доля единиц, обладающих изучаемым признаком.

Предельная ошибка выборки 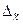–максимально возможное расхождение выборочной и генеральной средних, т. е. максимум ошибки при заданной вероятности её появления: .

Предельная ошибка выборочной доли: .

Множитель t в этих формулах называется коэффициентом доверия. Он представляет собой показатель кратности средней ошибки выборки и зависит от значения доверительной вероятности Р, с которой гарантируется величина предельной ошибки выборки.

В математической статистике доказывается, что вероятность появления заданной предельной ошибки подчиняется нормальному закону распределения, выражающемуся через функцию Лапласа. Значения функции Лапласа для разных t рассчитаны и имеются в специальных таблицах, из которых в статистике широко применяется сочетание:

Вероятность	0,683	0,866	0,950	0,954	0,988	0,990	0,997	0,999
t	1	1,5	1,96	2	2,5	2,58	3	3,5

Задавшись конкретным уровнем вероятности, выбирают величину коэффициента доверия t и определяют предельную ошибку выборки.

Тогда доверительный интервал для генеральной средней зависит от величины предельной ошибки выборки: .

Из вышесказанного следует, что лишь с определённой степенью вероятности можно утверждать, что показатели генеральной совокупности и их отклонения не превысят величину .

Аналогичным образом определяется доверительный интервал для генеральной доли: p .

Таким образом, чем больше величина предельной ошибки выборки, тем больше величина доверительного интервала и, следовательно, тем ниже точность оценки.

Следовательно, при выборочном наблюдении определяется не одно, точное значение обобщающей характеристики генеральной совокупности, а лишь её доверительный интервал с заданным уровнем вероятности. И это серьезный недостаток выборочного метода статистики.

В порядке случайной выборки исследован возраст 100 студентов вуза из общего числа 200 человек. Результаты обработки материалов наблюдения приведены в таблице:

Возраст, лет	17	18	19	20	21	22	23
Число студентов, чел.	11	13	18	23	17	10	8

Установить: 1) средний возраст студентов вуза по выборке;

2) величину ошибки при определении возраста студентов на основе выборки;

3) вероятные пределы колебания возраста для всех студентов при вероятности 0,997.

Решение:

1). Средний возраст студентов вуза (выборочная средняя) определяется по формуле средней арифметической взвешенной:

Дисперсия выборочной средней:

2). Средняя ошибка случайной выборки:

3). Предельная ошибка выборки (P=0,997, t=3):

4). Пределы колебания возраста студентов в генеральной совокупности:

Таким образом, средний возраст всех студентов вуза находится в пределах от 19,48 до 20,20 лет.

При 20%-м выборочном наблюдении (по способу случайной бесповторной выборки) населения города с численностью 380000 чел. установлено: удельный вес населения в возрасте до 16 лет составил 14%. Определить с вероятностью 0,954 пределы, в которых будет находиться доля этой группы населения в численности населения всего города.

Решение:

1). Зная объём генеральной совокупности и долю отбора (20%, или 0,2), находим объём выборки:

2). Средняя ошибка выборочной доли:

3). Предельная ошибка выборочной доли (P=0,954, t=2):

4). Доверительный интервал для генеральной доли:

Таким образом, доля населения в возрасте до 16 лет в общей численности населения города с вероятностью 95,4% находится в пределах от 13,775% до 14,225%, то есть составляет интервал от 52345 чел. до 54055 чел. из 380000 чел.

При выборочном обследовании 10 % изделий партии готовой продукции по методу бесповторного отбора получены следующие данные о содержании влаги в образцах.

Влажность, %	Число образцов, f_i	х_i
До 13	4	12
13 – 15	18	4
15 – 17	50	16
17 – 19	22	18
19 и выше	6	20
Итого:	100

Определить: средний % влажности, дисперсию, среднее квадратическое отклонение; с вероятностью 0,954 возможные пределы, в которых ожидается средний % влажности всей готовой продукции; с вероятностью 0,997 возможные пределы удельного веса стандартной продукции при условии, что к нестандартной партии относятся изделия с влажностью до 13 и выше 19%.

Решение: