Оригинальные способы решения арифметических задач

Различные способы решения арифметических задач;

По альтернативным методикам предлагаются разнообразные способы решения задач, например:

1) решение задач способом подбора;

2) решение задач методом целенаправленного перебора;

3) решение комбинаторных задач. При их решении пользуются графом.

4) графический способ решения

5) практический способ.

Приведем пример решения одной задачи разными способами из статьи Романовой Т.Д. «Решение задач разными способами».

Задача № 1. («Математика» Моро М.И. 1-3 № 20 с. 147). Две бригады рабочих должны посадить 490 деревьев. Сколько деревьев посадит каждая бригада, если распределить эту работу по числу рабочих и если в первой бригаде 34 рабочих, а во второй 36 рабочих.

Составим краткую запись в виде таблицы:

Производительность труда рабочего	Кол-во рабочих в бригаде	Объем выполненной работы
I	одинаковая	34 р.	? > 490 д. ?
II	36 р.

По данной краткой записи может видеть три способа ее решения.

1 способ. 1)34+36=70(р.) — всего рабочих в двух бригадах

2)490:70=7(д.) — производительность труда рабочего

3)34*7=238(д.) — посадит первая бригада

4)36*7=252(д.) — посадит вторая бригада

2 способ . 1)34+36=70(р.) — всего рабочих в двух бригадах

2)490:70=7(д.) — производительность труда рабочего

3)34*7=238(д.) — посадит первая бригада

4)490-238=252(д.) — посадит вторая бригада

3 способ . 1)34+36=70(р.) — всего рабочих в двух бригадах

2)490:70=7(д.) — производительность труда рабочего

3)36*7=252(д.) — посадит вторая бригада

4)490-252=238(д.) — посадит первая бригада.

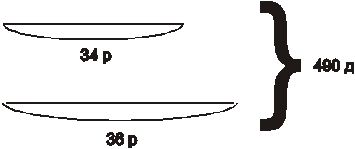Воспользуемся графической иллюстрацией для составления краткой записи:

Предположим, что число рабочих в каждой бригаде одинаковое и каждая бригада посадила деревьев поровну. Этот прием — выдвижение гипотезы — позволяет изменить схему.

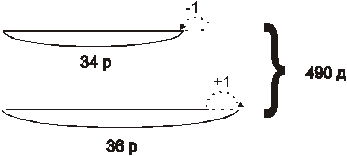Рис.2

Данная схема побуждает к следующим способам решения задач:

4 способ . 1)34+36=70(р.) — всего рабочих в двух бригадах

2)70:2=35(р.) — в каждой бригаде по предположению

3)490:2=245(д.) — посадила бы каждая такая бригада

4)245:35=7(д.) — производительность труда рабочего

5)34*7=238(д.) — посадит первая бригада

6)36*7=252(д.) — посадит вторая бригада

5 и 6 способы основаны на предположении о равночисленности рабочих в бригадах и, следовательно, на одинаковом объеме выполненных работ. 5 и 6 способы имеют первые три действия аналогичные первым трем действиям способа 4, а последние действия аналогичны действиям 3 и 4 в способах 2 и 3.

7 способ. Предположим только, что обе бригады посадили деревьев поровну. Тогда 1)490:2=245(д.) — могла бы посадить каждая бригада

2)34+36=70(р.) — всего рабочих в двух бригадах

3)490:70=7(д.) — производительность труда рабочего

4)245-7=238(д.) — посадит первая бригада рабочих

5)245+7=252(д.) — посадит вторая бригада

8 способ. Воспользуемся четность чисел и предположим, что рабочие выполняют предложенный объем работы в парах. Тогда

1)34:2=17(п.) — число пар рабочих в первой бригаде

2)36:2=18(п.) — число пар рабочих во второй бригаде

3)17+18=35(п.) — всего пар в двух бригадах

4)490: 35=14(д.) — производительность труда пары рабочих

5)14*17=238(д.) — посадит первая бригада

6)14*18=252(д.) — посадит вторая бригада

9 и 10 способы также основаны на предположении о выполнении объема работ по посадке деревьев рабочими в парах. Данные способы имеют первые четыре действия аналогичные первым четырем действиям способа 8.Последующие 5 и 6 действия могут быть такими:

Например для способа 9: 14*17=238(д.) — посадит первая бригада

490-238=252(д.) — посадит вторая бригада .

Для 10 способа: 18*14=252(д.) — посадит вторая бригада

490-252=238(д.) — посадит первая бригада.

Внесем изменения в схему:

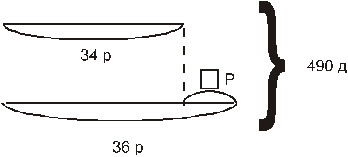Рис.3

Воспользуемся разностью в численности рабочих бригад .

11 способ. 1)36-34=2(р.) — разница

2)36+34=70(р.) — всего рабочих

3)490:70=7(д.) — производительность труда одного рабочего

4)7*2=14(д.) — посадят деревьев два рабочих

5)34*7=238(д.) — посадит первая бригада

6)238+14=252(д.) — посадит вторая бригада

12 способ. Рассуждения аналогичны рассмотренным в способе 11, но в пятом действии узнаем, сколько посадит деревьев вторая бригада 36*7=252(д.), а уже после найдем, сколько посадит деревьев первая бригада.

Рассмотренные способы называют арифметическим. В заключении

можно выделить еще два способа — алгебраический и графический.

13 способ(алгебраический). Пусть х — число деревьев, посаженных одним рабочим. Тогда две бригады посадят (34+36)*х. Всего надо посадить 490 деревьев.

Составим уравнение: (34+36)*х=490

Решая уравнение, находим, сколько деревьев посадит один рабочий:

х=7. Отсюда:7*34=238(д.) — посадит первая бригада

Источник

Решение текстовых задач арифметическим способом

Разделы: Математика

Обучение решению текстовых задач играет важную роль в формировании математических знаний. Текстовые задачи дают большой простор для развития мышления учащихся. Обучение решению задач – это не только обучение технике получения правильных ответов в некоторых типичных ситуациях, сколько обучение творческому подходу к поиску решения, накопление опыта мыслительной деятельности и демонстрация учащимися возможностей математики в решении разнообразных задач. Однако при решении текстовых задач в 5-6 классах чаще всего используется уравнение. Но мышление пятиклассников еще не готово к формальным процедурам, выполняемым при решении уравнений. Арифметический способ решения задач имеют ряд преимуществ по сравнению с алгебраическим потому, что результат каждого шага по действиям нагляднее и конкретнее, не выходит за рамки опыта пятиклассников. Школьники лучше и быстрее решают задачи по действиям, чем с помощью уравнений. Детское мышление конкретно, и развивать его надо на конкретных предметах и величинах, затем постепенно переходить к оперированию абстрактными образами.

Работа над задачей предусматривает внимательное прочтение текста условия, вникания в смысл каждого слова. Приведу примеры задач, которые легко и просто можно решить арифметическим способом.

Задача 1. Для приготовления варенья на две части малины берут три части сахара. Сколько килограммов сахара нужно взять на 2 кг 600 г малины?

При решении задачи на “части” надо приучить наглядно представлять условие задачи, т.е. лучше опираться на рисунок.

1. 2600:2=1300 (г) — приходится на одну часть варенья;
2. 1300*3= 3900 (г) — сахара нужно взять.

Задача 2. На первой полке стояло в 3 раза больше книг, чем на второй. На двух полках вместе стояло 120 книг. Сколько книг стояло на каждой полке?

1) 1+3=4 (части) — приходится на все книги;

2) 120:4=30 (книг) — приходится на одну часть ( книги на второй полке);

3) 30*3=90 (книг)- стояло на первой полке.

Задача 3. В клетке сидят фазаны и кролики. Всего в ней 27 голов и 74 ноги. Узнать число фазанов и число кроликов в клетке.

Представим, что на крышку клетки, в которой сидят фазаны и кролики, мы положили морковку. Тогда все кролики встанут на задние лапки, чтобы дотянуться до нее. Тогда:

1. 27*2=54 (ноги) — будут стоять на полу;
2. 74-54=20 (ног) — будут наверху;
3. 20:2=10 (кроликов);
4. 27-10=17 (фазанов).

Задача 4. В нашем классе 30 учащихся. На экскурсию в музей ходили 23 человека, а в кино – 21, а 5 человек не ходили ни на экскурсию, ни в кино. Сколько человек ходили и на экскурсию, и в кино?

Для анализа условия и выбора плана решения можно использовать “круги Эйлера”.

1. 30-5=25 (человек) – ходили или в кино, или на экскурсию,
2. 25-23=2 (человек) – ходили только в кино;
3. 21-2=19 ( человек) – ходили и в кино, и на экскурсию.

Задача 5. Три утенка и четыре гусенка весят 2 кг 500 г, а четыре утенка и три гусенка весят 2кг 400г. Сколько весит один гусенок?

1. 2500+2400=2900 (г) – весят семь утят и семь гусят;
2. 4900:7=700 (г) – вес одного утенка и одного гусенка;
3. 700*3=2100 (г) – вес 3 утят и 3 гусят;
4. 2500-2100=400 (г) – вес гусенка.

Задача 6. Для детского сада купили 20 пирамид: больших и маленьких – по 7 и по 5 колец. У всех пирамид 128 колец. Сколько было больших пирамид?

Представим, что со всех больших пирамид мы сняли по два кольца. Тогда:

1) 20*5=100 (колец) – осталось;

2) 128-100-28 (колец) – мы сняли;

3) 28:2=14 (больших пирамид).

Задача 7. Арбуз массой 20кг содержал 99% воды. Когда он немного усох, содержание воды в нем уменьшилось до 98%. Определите массу арбуза.

Для удобства решение будет сопровождаться иллюстрацией прямоугольников.

99% вода	1% сухое вещество
98% вода	2% сухое вещество

При этом желательно рисовать прямоугольники “сухого вещества” равными, потому что масса “сухого вещества” в арбузе остается неизменной.

1) 20:100=0,2 (кг) – масса “сухого вещества”;

2) 0,2:2=0,1 (кг) – приходится на 1% усохшего арбуза;

3) 0,1*100=10 (кг) – масса арбуза.

Задача 8. Гости спросили: сколько лет исполнилось каждой из трех сестер? Вера ответила, что ей и Наде вместе 28 лет, Наде и Любе вместе 23 года, а всем троим 38 лет. Сколько лет каждой из сестер?

1. 38-28=10 (лет) – Любе;
2. 23-10=13 (лет) – Наде;
3. 28-13=15 (лет) – Вере.

Арифметический способ решения текстовых задач учит ребенка действовать осознанно, логически правильно, потому что при решении таким способом усиливается внимание к вопросу “почему” и имеется большой развивающий потенциал. Это способствует развитию учащихся, формированию у них интереса к решению задач и к самой науке математике.

Чтобы сделать обучение посильным, увлекательным и поучительным, надо очень внимательно отнестись к выбору текстовых задач, рассматривать различные способы их решения, выбирая оптимальные из них, развивать логическое мышление, что в дальнейшем необходимо при решении геометрических задач.

Научиться решать задачи школьники смогут, лишь решая их. “Если вы хотите научиться плавать, то смело входите в воду, а, если хотите научиться решать задачи, то решайте их”,- пишет Д.Пойа в книге “ Математическое открытие”.

Источник

Обучение младших школьников решению нестандартных арифметических задач

Обучение младших школьников решению нестандартных арифметических задач

Решение арифметических задач, особенно нестандартных, позволяет приучать млад- ших школьников к правильности и четкос- ти рассуждений, к критическому осмысле- нию полученных результатов; развивает у них гибкость, вариативность мышления.

Учителя включают нестандартные ариф- метические задачи в уроки математики, предлагают для домашней самостоятельной работы, используют во внеклассной работе с учениками. Однако результативность такой работы иногда оказывается не столь высо- кой, как хотелось бы. При выполнении олимпиадных работ ученики не могут само- стоятельно решить задачу, у них возникают трудности при оформлении решения.

Эффективность обучения младших школьников решению нестандартных задач зависит, на наш взгляд, от нескольких усло- вий. Во-первых, задачи следует вводить в процесс обучения в определенной системе с постепенным нарастанием сложности, так как непосильная задача мало повлияет на развитие учащихся. Во-вторых, необходи- мо предоставлять ученикам максимальную самостоятельность в поиске решения задач, давать возможность пройти до конца по не- верному пути, убедиться в ошибке, вер-

нуться к началу и искать другой, верный путь решения. В-третьих, нужно помочь учащимся осознать некоторые способы, приемы, общие подходы к решению нестан- дартных арифметических задач. Предлагае- мые в данной статье приемы описаны в ме- тодической литературе (см. список литера- туры), и с ними, безусловно, должен быть знаком учитель. С некоторыми способами поиска путей решения нестандартных задач учитель может познакомить учащихся.

Как показала школьная практика, обуче- ние младших школьников решению нестан- дартных арифметических задач можно раз- делить на два этапа. На первом этапе прово- дится специальная работа по выводу и ос- мыслению общих подходов к решению таких задач. При этом важно, чтобы учени- ки уже усвоили процесс решения любой арифметической задачи (читаю задачу; вы- деляю, что известно и что надо узнать, и т.д.); познакомились с приемами работы на каждом этапе решения задачи (виды наг- лядной интерпретации, поиска решения, проверки решения задачи и др.). На втором этапе учащиеся применяют ранее сформу- лированные общие приемы в ходе самостоя- тельного поиска решения конкретных задач.

Опишем, как можно провести работу на первом этапе. В описании методики рабо- ты будем выделять серии задач. Задачи од- ной серии будут подчинены определенной цели. Первая задача серии решается под руководством учителя (чаще всего она бо- лее сложная, чем другие задачи серии), она служит для выведения приема или спосо- ба, который помогает решить задачу. На следующих задачах дети упражняются в применении приема, который они сформу- лировали, и выделяют некоторые ориенти- ры, помогающие определить, в каких слу- чаях удобно использовать данный способ или прием.

Задачи серий I–III позволяют сформу- лировать первую рекомендацию для уча- щихся при решении нестандартных задач: для того чтобы решить задачу, бывает по- лезно построить к ней рисунок или чертеж. Следует начинать с этой рекомендации, так как ученики уже делали такой вывод при решении стандартных задач. Но в дан- ном случае должны быть выделены неко- торые особенности использования графи- ческих изображений. Во-первых, ответ, а в некоторых случаях часть неизвестных мо- гут быть получены только из чертежа без выполнения арифметических действий. Во-вторых, иногда нужно будет делать до- полнительные построения, т.е. в процессе решения задачи будут выполнены новые чертежи с учетом найденных чисел. Чер- теж будет использоваться также и при применении других приемов нестандарт- ных задач.

Задача 1. Бревно длиной 12 м распи- лили на 6 равных частей. Сколько распилов сделали?

После чтения задачи ученикам предла- гается ответить на вопрос, решали ли они задачи такого вида и известен ли им способ решения таких задач.

Возможно, некоторые ученики ошибоч- но будут считать, что знают, как решить за- дачу: «Надо 12 м разделить на 6 равных час- тей». Учитель должен дать учащимся воз- можность найти результат, оценить его и убедиться в ошибке. (Разделив 12 на 6, мы узнали, что длина одной части равна 2 м. Но в задаче спрашивается не какова длина

одной части, а сколько сделали распилов. Следовательно, задача решена неправиль- но.) Затем ученики могут вновь прийти к ошибочному заключению: «Сколько час- тей, столько и распилов». Учитель предла- гает проверить найденный ответ, сделав ус- ловный рисунок или чертеж. Ученики обоз- начают бревно прямоугольником или от- резком длиной 12 клеточек, делят его вертикальными засечками на 6 равных час- тей. Подсчитав число полученных засечек (распилов), они убеждаются, что их 5, а не 6, как они считали раньше. Эту задачу ре- шили, не выполняя арифметических дейс- твий. Ответ получили, построив чертеж (рисунок). Под ним ученики записывают ответ задачи. Таким образом, учащиеся приходят к следующему выводу: при поиске решения незнакомой задачи полезно сделать чертеж (рисунок), так как работа с черте- жом (рисунком) может являться способом решения задачи.

Решение нижеследующих задач будет

способствовать подтверждению вывода, сделанного при поиске решения первой за- дачи. Учитель ставит перед учащимися сле- дующую учебную задачу: научиться решать арифметические задачи с помощью постро- ения графических изображений.

Задача 2. Лестница состоит из 9 ступе- нек. На какую ступеньку надо встать, чтобы оказаться на середине лестницы? (На пя- тую ступеньку.)

Задача 3. Маша и Петя встретились в вагоне электропоезда. Маша всегда садится в пятый вагон от начала поезда, а Петя — в пятый вагон от конца поезда. Сколько ваго- нов в поезде? (9 вагонов.)

Задача 4. Вдоль одной стороны огоро- да надо поставить изгородь. Длина огорода 10 м. Сколько потребуется столбов, чтобы поставить их по длине огорода на расстоя- нии 2 м друг от друга? (6 столбов.)

Задача 5. 3 одинаковые ватрушки надо разделить поровну между 4 детьми. Как это сделать, выполнив наименьшее число раз- резов? (2 ватрушки разрезать пополам, а третью — на 4 равные части.)

Решая следующие задачи, можно под- вести учащихся к мысли о том, что в неко- торых случаях часть данных целесообразно

найти с помощью графических изображе- ний (рисунков, чертежей), а часть — с помо- щью арифметических действий.

Задача 6. Ширина занавески для окна равна 1 м 20 см. Надо пришить 6 колец на одинаковом расстоянии друг от друга (пер- вое и последнее кольца должны распола- гаться по краям занавески). Сколько санти- метров надо оставлять между кольцами?

Следуя ранее выведенной рекоменда- ции, ученики начинают делать схематичес- кий чертеж к данной задаче. Они показыва- ют засечкой первое кольцо, откладывают отрезок любой выбранной длины, ставят

мается на 18 м, а за ночь сползает вниз на 12 м. Сколько дней нужно муравью, чтобы выбраться из колодца?

Самостоятельно решая эту задачу, уча- щиеся могут сделать следую-

щий чертеж (рис. 1) и неверно решить задачу:

1) 18 – 12 = 6 (м) — подни- мается муравей за сутки.

2) 30 : 6 = 5 (сут.) — потре- буется муравью, чтобы вы- браться из колодца.

Учитель предлагает: а) про- верить решение, показав на от-

вторую засечку, откладывают отрезок та-

дельных чертежах положение

кой же длины, как первый, ставят третью засечку и так действуют до тех пор, пока не поставят 6 засечек. По полученному схема- тическому чертежу подсчитывают число равных частей, на которые 6 колец разделят занавеску.

Для того чтобы ответить на вопрос зада- чи, остается разделить всю ширину занавес- ки на 5 равных частей: 120 : 5 = 24 (см).

Такая же идея используется учениками при самостоятельном решении следующих задач этой серии.

Задача 7. Вдоль беговой дорожки че- рез одинаковое расстояние вкопаны стол- бы. Старт дан у 1-го столба. Через 12 минут бегун был у 4-го столба. Через сколько ми- нут от начала старта бегун будет у 7-го столба, если он бежит с одинаковой скорос- тью? (Через 24 минуты.)

Задача 8. Имеются бревна длиной 4 м и 5 м одинаковой толщины. Бревно перепи- ливается за 1 минуту. Надо напилить 60 бревен длиной 1 м. Можно пилить только 4-метровые или только 5-метровые бревна. Какие бревна надо пилить, чтобы работу за- кончить раньше? Сколько времени тогда можно сэкономить? (Надо пилить 4-метро- вые бревна, можно сэкономить 3 минуты.)

Следует также показать учащимся, что иногда в процессе решения задачи нужно делать дополнительные построения или пе- рестраивать чертежи с учетом найденных чисел. Это можно сделать при решении сле- дующей задачи.

Задача 9. Муравей находится на дне колодца глубиной 30 м. За день он подни-

муравья в каждый день; б) в ходе решения подсчитывать, сколько метров остается му- равью, чтобы выбраться из колодца.

Таким образом, ученики видят, что в третий день муравей поднимется на 18 м и выберется из колодца. Значит, сначала они решили задачу неправильно. А найти верный ответ им помогло последователь- ное построение нескольких чертежей, от- ражающих те изменения, которые проис- ходили в реальной ситуации, описывае- мой в задаче.

В следующих задачах закрепляется вы- веденный прием решения.

Задача 10. Дети едут на экскурсию в трех автобусах. Во второй автобус село на 5 человек больше, чем в первый, а в третий — на 7 человек меньше, чем во второй. Сколь- ко детей из второго автобуса должно пере- сесть, чтобы в каждом автобусе детей стало поровну? (В первый автобус — 1 человек, в третий — 3 человека.)

Задача 11. 10 слив имеют такую же массу, как 3 яблока и 1 груша, а 2 сливы и 1

яблоко — как 1 груша. Сколько слив нужно взять, чтобы их масса была равна массе 1 груши? (4 сливы.)

Задачи серии IV позволяют вывести сле- дующую рекомендацию для учащихся при решении нестандартных задач: для того чтобы решить задачу, бывает нужно ввести вспомогательный элемент (часть).

Задача 12. Разложи 45 шариков в 4 коробки так, что если число шариков в третьей коробке увеличить в 2 раза, а в четвертой уменьшить в 2 раза, а в первой и второй оставить без изменения, то в каж- дой коробке будет одинаковое число ша- риков.

Сначала учащиеся выполняют первый схематический чертеж (рис. 3).

Анализируя чертеж, ученики замечают, что на нем есть отрезки одинаковой длины, но не все. Учитель предлагает дорисовать чертеж, чтобы все отрезки состояли из оди- наковых частей (рис. 4). Затем сообщает, что в таких случаях можно ввести вспомо- гательный элемент — часть. Примем число шариков в третьей коробке за 1 часть, тогда число шариков в четвертой коробке соста- вит 4 части, в первой — 2 части, во второй — 2 части. Затем выполняется арифметичес- кое решение:

1) 2 + 2 + 1 + 4 = 9 (ч.) — составляют 45 шариков.

2) 45 : 9 = 5 (ш.) — содержится в 1 части или число шариков в третьей коробке.

3) 5 · 2 = 20 (ш.) — число шариков в пер- вой или во второй коробке.

4) 5 · 4 = 20 (ш.) — число шариков в чет- вертой коробке.

В процессе поиска решения данной за- дачи использовали несколько приемов: строили и достраивали чертеж, вводили вспомогательный элемент. Его удобно ввес- ти, когда на чертеже получены отрезки оди- наковой длины.

В следующих задачах ученики будут уп- ражняться в решении задач с помощью вве- дения вспомогательного элемента.

Задача 13. Веревку разрезали на 2 кус- ка так, что один кусок оказался в 4 раза длиннее другого. Чему равна длина верев- ки, если один кусок длиннее другого на 18 см? (30 см)

Задача 14. Одного крестьянина спро- сили, сколько у него денег. Он ответил:

«Мой брат втрое богаче меня, отец втрое богаче брата, дед втрое богаче отца, а у всех у нас ровно 100 000 рублей. Узнайте, сколь- ко у меня денег». (2 500 рублей.)

В задачах серии V выводится еще одна рекомендация для учащихся при решении нестандартных задач: в поиске ответа на вопрос задачи можно использовать способ подбора.

Задача 15. Сумма четырех различных чисел равна 13. Наименьшее из этих чисел на 5 меньше наибольшего. Найди эти числа.

Сначала ученики выполняют чертеж (рис. 5).

Затем учащиеся пытаются преобразо- вать чертеж, чтобы получить одинаковые числа, как они делали в предыдущих зада- чах. Ученики приходят к выводу, что этого сделать нельзя, так как в условии ничего не говорится о числовых отношениях между вторым и третьим числом. Встает проблема: можно ли решить эту задачу? Может быть, в ней не хватает данных? Учитель предла- гает использовать для решения этой задачи способ подбора.

Рассуждения удобнее начать с наимень- шего из чисел.

— Пробуем число 0. Тогда получаем: 0 + ☐ + ☐ + 5 = 13. Подберем пропущенные

числа. Их сумма равна 13 – 5 – 0 = 8. Эти числа должны быть разными и быть больше 0, но меньше 5. Между 0 и 5 идут числа 1, 2, 3, 4. Среди них нельзя выбрать два разных

числа, дающих в сумме 8. Значит, число 0 не подходит.

Пробуем число 1. Тогда получаем: 1 + ☐ + ☐ + 6 = 13. Подбираем пропущен — ные числа . Их сумма равна : 13 – 1 – 6 = 6.

Между числами 1 и 6 стоят числа 2, 3, 4, 5. Среди них выбираем два, дающих в сумме

6. Это числа 2 и 4. Проверяем, правильно ли мы нашли четыре числа. Для этого скла- дываем их: 1 + 2 + 4 + 6 = 13. Получили сумму, данную в задаче. Другие условия также соблюдены: числа различные, наи- меньшее из этих чисел 1, оно на 5 меньше наибольшего числа 6.

Получив один ответ, нужно проверить, нет ли других вариантов ответа. Для этого пробуем число 2. Тогда получаем: 2 + ☐ +

+ ☐ + 7 = 13. Подбираем пропущенные чис —

ла. Их сумма равна 4. Среди чисел 3, 4, 5, 6 нельзя выбрать два числа, дающих в сумме 4 (сумма любых двух перечисленных чисел больше 4). Можно проверить число 3 та- ким же образом. Числа, начиная с 4, прове- рять не нужно, так как сумма двух чисел получается равной или больше: 13 : 4 + ☐ +

Получаем ответ задачи: числа 1, 2, 4, 6.

В итоге важно подчеркнуть, что задачу решили, подбирая нужные числа. Делали это так: последовательно рассматривали различные возможные варианты и выбра- ли те, которые соответствуют всем усло- виям задачи. Чертеж помогал выделить эти условия из текста задачи. В некоторых случаях перебор удобно начинать не с на- именьшего, а с наибольшего возможного числа. Иногда, оценив полученный ре- зультат, можно пропустить некоторые числа. Этот способ удобно использовать, когда число возможных вариантов не- большое.

При решении следующих задач учени- ки упражняются в применении способа подбора.

Задача 16. Сумма трех разных дву- значных чисел равна 34. Какие это числа? (10, 11, 13)

Задача 17. Трое ребят были на рыбал- ке. Вместе они поймали 14 рыб. Андрей поймал меньше всех рыб. Дима поймал в 3 раза больше рыб, чем Вова. Сколько рыб поймал каждый мальчик? (Вова поймал 3

рыбы, Дима поймал 9 рыб, Андрей поймал 2 рыбы.)

Задача 18. Внучке, маме и бабушке вместе 114 лет. Сколько лет в отдельности внучке, маме и бабушке, если возраст каж- дой выражается двузначным числом, оканчивающимся одной и той же цифрой? (Внучке 18 лет, маме 38 лет, бабушке 58 лет.)

В задачах серии VI выводится следую- щая рекомендация при решении нестан- дартных задач: полезно переформулировать задачу, т.е. сказать ее другими словами, чтобы она стала знакомой и понятной. При этом в большинстве случаев будет происходить перевод текста задачи на язык математики.

Задача 19. Число яблок в корзине двузначное. Эти яблоки можно раздать по- ровну 2, 3 или 5 детям, но нельзя раздать поровну 4 детям. Сколько яблок в корзине? (Укажите такое наименьшее двузначное число.)

Сначала ученики пытаются сделать ри- сунок или чертеж к задаче, но испытывают затруднения, так как на чертеже трудно по- казать, что нельзя раздать яблоки поровну 4 детям, следовательно, непонятно, как ис- пользовать чертеж для решения задачи. Тогда ученики начинают применять способ подбора. Учитель предлагает сначала изме- нить формулировку задачи, чтобы легче было выполнить перебор. Выясняется, что если яблоки можно раздать поровну 2, 3 и 5 детям, значит, число яблок делится на 2, 3,

5. Если яблоки нельзя раздать 4 детям по- ровну, значит, число яблок не делится на 4. Задачу переформулируют следующим об- разом: «Найди наименьшее двузначное число, которое делится на 2, 3, 5 и не делит- ся на 4».

Далее выполняется перебор. Ученики проверяют наименьшее двузначное число

10. Оно делится на 2 и 5, но не делится на 3, значит, число 10 не подходит. Перебор можно сократить, не рассматривать все чис- ла подряд, а проверять только числа, деля- щиеся на 5. Число 15 не подходит, так как не делится на 2. Так ученики доходят до числа 30, которое делится на 2, 3, 5 и не де- лится на 4. Значит, в корзине 30 яблок.

Данную задачу можно было бы решить, выполняя чертеж. Начертить в тетради луч и откладывать на нем последователь- но отрезки длиной 2, 3, 5 клеточек, найти точку, в которой соединяются концы от- резков трех видов, подсчитать число кле- ток от начала луча до этой точки. На чер-

теже следовало бы проверить, что отрезки длиной 4 клеточки не укладываются целое число раз в большом отрезке длиной 30 клеток. И только тогда назвать ответ зада- чи. Этот способ трудоемкий, но он может оказаться более легким для некоторых учеников в силу их индивидуальных осо- бенностей.

В следующих задачах используется при- ем переформулирования задачи, а затем они решаются известными учащимся спо- собами.

Задача 20. Если конфеты расклады- вать по 2, 3, 4, то всегда остается 1 лишняя конфета. А если их раскладывать по 5, то лишних конфет нет. Сколько конфет, если их меньше 50? (25 конфет.)

Задача 21. В детском саду 100 детей. Для каждого ребенка купили альбом, крас- ки, кисточку. Продавец выписал чек на 3 750 рублей. Докажи, что при подсчете общей стоимости покупки допущена ошибка, если цены предметов выражались целым числом рублей. (Для нахождения общей стоимости цену набора надо умно- жить на 100, поэтому в результате должно получиться число, оканчивающееся двумя нулями, а число 3 750 оканчивается одним нулем.)

В задачах серии VII выводится следую- щая рекомендация при решении нестандарт- ных задач: условие или вопрос задачи можно разделить на части и решить задачу по частям.

Задача 22. В два автобуса сели 123 экскурсанта. Затем из одного автобуса вышли 8 человек. Трое из них сели в другой автобус, а остальные поехали на машине. После этого в автобусах стало пассажиров поровну. Сколько пассажиров было в каж- дом автобусе сначала?

По усвоенной первой рекоменда- ции ученики вначале делают к задаче чер- теж.

Учитель предлагает решать эту задачу, разбив ее на части, чтобы облегчить реше- ние. Ученики читают первые три предложе- ния из текста задачи и думают, что по этим данным можно узнать.

1) 8 – 3 = 5 (чел.) — поехали на машине.

2) 123 – 5 = 118 (чел.) — остались в каж- дом автобусе.

Затем решают задачу дальше:

3) 118 : 2 = 59 (чел.) — стало в каждом автобусе.

Чтобы легче было сформулировать пос- леднюю часть задачи, можно переделать чертеж с учетом найденных данных. Учени- ки формулируют: «Из одного автобуса вышли 8 человек, и в нем осталось 59 чело- век. В другой автобус сели 3 человека, и в нем стало 59 человек. Сколько человек бы- ло в каждом автобусе сначала?» — и закан- чивают решение:

4) 59 + 8 = 67 (чел.) — было в первом ав- тобусе.

5) 59 – 3 = 56 (чел.) — было во втором автобусе.

Иногда полезно разделить на части не условие, а вопрос задачи. Так можно посту- пить при решении следующей задачи.

Задача 23. 18 ручек стоят на 30 рублей больше, чем 30 карандашей. Те же 18 ручек стоят на 10 рублей больше, чем 40 таких же карандашей. Сколько стоят 1 карандаш и

Сначала ученики выполняют к задаче чертеж.

Затем, используя чертеж, отвечают сна- чала на первый вопрос: «Сколько стоит 1 карандаш?»

1) 40 – 30 = 10 (шт.) — разница в коли- честве карандашей.

2) 30 – 10 = 20 (р.) — стоят 10 каранда- шей.

3) 20 : 10 = 2 (р.) — стоит 1 карандаш. После этого можно ответить на второй

вопрос: «Сколько стоит 1 ручка?»

4) 2 · 30 = 60 (р.) — стоят 30 карандашей. 5) 60 + 30 = 90 (р.) — стоят 18 ручек.

6) 90 : 18 = 5 (р.) — стоит 1 ручка.

Данный прием используется в задачах с больши м числом разных объектов или

действий с ними, с несколькими вопроса- ми. В следующих задачах также можно ис- пользовать прием разбиения задачи на части.

Задача 24. На двух кустах сидели 16 воробьев. Со второго куста улетели 2 воро- бья, а затем с первого куста на второй пере- летели 5 воробьев. После этого на каждом кусте оказалось одно и то же число воро- бьев. Сколько воробьев было вначале на каждом кусте? (12 и 4 воробья.)

Задача 25. Три подружки договори- лись купить к праздничному столу 12 пи- рожных. Первая купила 5 штук, вторая — 7, а третья вместо своей доли пирожных внес- ла 12 рублей. Как подружки должны разде- лить между собой эти деньги, если все пи- рожные были по одинаковой цене? (3 рубля и 9 рублей.)

С помощью задач серии VIII можно вы- вести следующую рекомендацию при ре- шении нестандартных задач: решать зада- чу можно, начиная «с конца».

Задача 26. Мать троих сыновей оста- вила утром тарелку слив. Первым прос- нулся старший сын, съел третью часть слив и ушел. Вторым проснулся средний сын, он съел третью часть того, что было на тарелке, и ушел. Позднее всех встал младший сын. Он съел также третью часть слив. После этого на тарелке осталось 8 слив. Сколько слив мать утром положила на тарелку?

Ученики выполняют чертеж (рис. 8). Учитель предлагает начать решать зада-

чу «с конца», так как известно, сколько

слив осталось в конце, когда три брата съе- ли сливы. Из чертежа видно, что 8 слив — это —²3 всех слив, которые были в тарелке, когда встал младший сын. Найдем, сколько слив было в тарелке, когда встал младший сын: 8 : 2 · 3 = 12 (сл.). Подпишем это число на втором отрезке (рис. 9). Из чертежа ви-

дим, что 12 слив — это —²3 всех слив, которые были в тарелке, когда встал средний сын. Найдем, сколько слив было в тарелке, когда встал средний сын: 12 : 2 · 3 = 27 (сл.). Дела- ется вывод о том, что, решая «с конца», пос- ледовательно пришли к тому, что было в са- мом начале. Прием используется, когда в задаче известно число, полученное в конце выполнения каких-либо действий.

В следующих задачах ученики упражня- ются в решении задач «с конца».

Задача 27. Мальчик задумал число. Умножил его на 3, из полученного произве- дения вычел 10, затем к результату приба- вил 16. У него получилось 21. Какое число задумал мальчик? (5)

Задача 28. Девочка начертила 4 отрез- ка. Каждый следующий отрезок она делала на 2 см длиннее предыдущего. Найди длину первого отрезка, если длина четвертого от- резка равна 12 см. (6 см)

Задача 29. У моста через речку встрети- лись лодырь и волшебник. Лодырь стал жа- ловаться на свою бедность. В ответ волшеб-

ник предложил: «Каждый раз, как ты перей- дешь этот мост, деньги у тебя удвоятся. Но каждый раз, перейдя мост, ты должен будешь отдать мне 24 копейки. Согласен?» Три раза переходил лодырь по мосту. А когда посмот- рел в кошелек, там ничего не осталось. Сколько денег было у лодыря? (21 копейка.) Сформулированные рекомендации по решению нестандартных задач объединя-

ются в следующей памятке.

Если тебе трудно решить задачу, то по- пробуй:

1) сделать к задаче рисунок или чертеж; подумай, может быть, нужно сделать на них дополнительные построения или изменить чертеж в процессе решения задачи;

2) ввести вспомогательный элемент (часть);

3) использовать для решения задачи способ подбора;

4) переформулировать задачу другими словами, чтобы она стала более понятной и знакомой;

5) разделить условие или вопрос задачи на части и решить ее по частям;

6) начать решение задачи «с конца».

Важно объяснить детям, что данные указания носят рекомендательный харак- тер. Необязательно применять их в той пос- ледовательности, как они записаны в па- мятке, необязательно выполнять все реко- мендации при решении одной задачи, мож- но комбинировать их в разных сочетаниях. В этом суть творческого процесса решения нестандартных задач. Можно показать это учащимся при совместном решении нес- кольких задач.

Задача 30. В семье 12 детей. Они соб- рали в лесу 70 орехов. Половину всех оре- хов мама раздала дочерям поровну. Осталь- ные она отдала сыновьям, которые раздели- ли их между собой также поровну. Каждый мальчик получил на 2 ореха больше, чем каждая девочка. Сколько у мамы дочерей и сыновей?

Сначала можно выделить следующую часть условия: «Собрали в лесу 70 орехов. Половину всех орехов мама раздала доче- рям, остальные — сыновьям». Отсюда узна- ем, что все дочери получили 70 : 2 = 35 (ор.) и сыновья также получили 35 орехов.

Затем выделяется вторая часть усло- вия: «В семье 12 детей. Все дочери получи- ли 35 орехов. И все сыновья получили 35 орехов. Мальчики и девочки разделили орехи поровну». Отсюда заключаем, что число сыновей и число дочерей — это чис- ла, которые в сумме дают число 12, и чис- ло 35 делится на каждое из них без остат- ка. Таким образом, мы переформулирова- ли условие, сказали его другими словами. Теперь будем использовать способ подбо- ра. Число 35 делится на 5, 7, 1, 35. Подхо- дят числа 5 и 7, так как их сумма равна 12. Остается решить, кого было 5 — сыно- вей или дочерей? Используем последнюю часть условия: «Каждый мальчик получил на 2 ореха больше, чем каждая девочка». Все девочки получили 35 орехов, все мальчики получили 35 орехов, если каж- дому мальчику досталось орехов больше, значит, мальчиков меньше, чем девочек.

Получаем ответ задачи: в семье 5 сыновей и 7 дочерей.

После работы, проведенной на первом этапе, можно перейти ко второму, на кото- ром учащиеся самостоятельно решают не- стандартные задачи. Приведем примеры нестандартных задач.

Задача 31. В магазине расфасовали картофель в 16 пакетов по 5 кг и по 3 кг. Масса всех пакетов по 5 кг оказалась равной массе всех пакетов по 3 кг. Сколько было па- кетов по 5 кг и сколько было пакетов по 3 кг? (6 пакетов по 5 кг и 10 пакетов по 3 кг.)

Задача 32. Мама испекла пирожки. Утром она съела 1 пирожок, а половину всех оставшихся пирожков положила в корзинку Красной Шапочке, чтобы она их отнесла бабушке. По дороге Красная Ша- почка съела 2 пирожка и третью часть ос- тавшихся пирожков отдала Волку. Бабушке Красная Шапочка принесла 8 пирожков. Сколько пирожков испекла мама? (29 пи- рожков.)

Задача 33. Периметр треугольника ра- вен 18 см. Первая сторона на 4 см короче второй, а вторая на 1 см короче третьей. Найди длину каждой стороны треугольни- ка, если длины выражаются целым числом сантиметров. (3 см, 7 см, 8 см)

Задача 34. У двоих мальчиков было вместе 8 груш. Когда один мальчик съел 1

грушу, а другой — 3 груши, груш стало по- ровну. Сколько груш было у каждого маль- чика? (3 и 5 груш.)

Задача 35. Имеется 6 шаров трех цве- тов. Желтых шаров больше, чем красных, и зеленых шаров больше, чем красных. Сколько шаров каждого цвета? (1 крас- ный шар, 2 зеленых и 3 желтых.)

Задача 36. Мальчик считал камушки, но потом забыл, сколько их было. Помнил только, что, когда считал парами, один ка- мушек был лишним, когда считал по четы- ре — тоже один камушек был лишним. Ког- да считал по пять — ни одного лишнего ка- мушка не было. Сколько было камушков, если их больше 10, но меньше 40? (25 ка- мушков.)

Задача 37. В трех клетках 8 кроликов. В первой столько, сколько во второй, а в третьей столько, сколько в первой и во второй вместе. Сколько кроликов в каждой клетке? (2, 2 и 4 кролика.)

Задача 38. За несколько одинаковых тетрадей заплатили 51 рубль. Сколько сто- ит 1 тетрадь, если их купили больше 10, но меньше 50? Цена тетради выражается це- лым числом рублей. (3 рубля.)

Задача 39. В токарном цехе завода вы- тачивают детали из металлических загото- вок. Из одной заготовки получается 1 де- таль. При изготовлении деталей получают- ся стружки, которые переплавляются в но- вые заготовки. Из стружек, полученных при изготовлении четырех деталей, вып- лавляется 1 новая заготовка. Сколько дета- лей можно сделать таким образом из 16 ме- таллических заготовок? (21 деталь.)

Задача 40. После того как 3 человека съели по одинаковому кусочку торта пря- моугольной формы, длина и ширина торта уменьшились в 2 раза. На сколько еще че- ловек хватит оставшегося торта, если все будут есть такие же кусочки, как и первые 3 человека? (Оставшегося торта хватит на 1 человека.)

Задача 41. На площадке играли 7 де- вочек и 2 мальчика. Сумма возрастов всех

играющих составила 80 лет. Все девочки были одногодки. Одинакового возраста бы- ли и мальчики. Когда в одну группу объеди- нились 5 девочек, а в другую все остальные, то оказалось, что суммы числа лет играю- щих в одной группе и другой стали равны- ми. Какого возраста были играющие? (Воз- раст каждой девочки — 8 лет, возраст каж- дого мальчика — 12 лет.)

Рамки статьи не позволяют подробно из- ложить методику обучения младших школь- ников решению нестандартных арифмети- ческих задач. Мы высказали только основ- ные идеи по поводу соответствующей рабо- ты, привели примеры задач.

Предлагаемые в статье материалы раз- рабатывались для учащихся выпускных классов начальной школы, апробированы учителями Санкт-Петербурга. Но, по мне- нию учителей, такая работа может и дол- жна начинаться с I класса, что требует про- ведения дальнейших исследований.

Волкова С.И. Задания развивающего характе- ра в новом едином учебнике «Математика»// Начальная школа. 1997. № 9.

Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка. М., 1988.

Кордемский Б.А. Математическая смекалка.

Кордемский Б.А., Ахадов А.А. Удивительный мир чисел: Математические головоломки и зада- чи для любознательных. М., 1996.

Левитас Г.Г. Нестандартные задачи в курсе математики начальной школы// Начальная школа. 2001. № 5.

Николау Л.Л. Задачи повышенной трудности

Радченко В.П. Способ подбора при решении задач// Там же. № 11–12.

Русанов В.Н. Математические олимпиады для младших школьников. М., 1990.

Труднев В.П. Внеклассная работа по матема- тике в начальной школе. М., 1975.

Фридман Л.Н., Турецкий Е.Н. Как научиться решать задачи. М., 1989.

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Источник