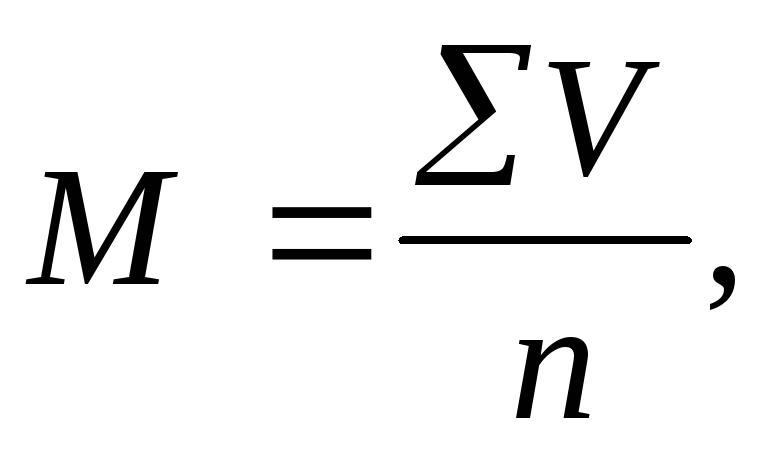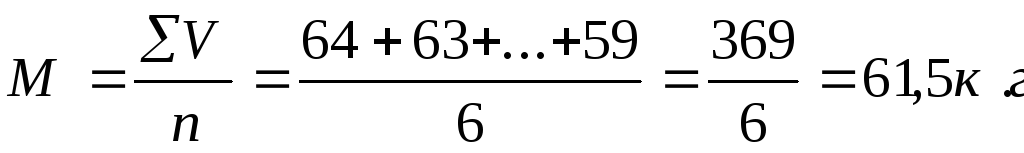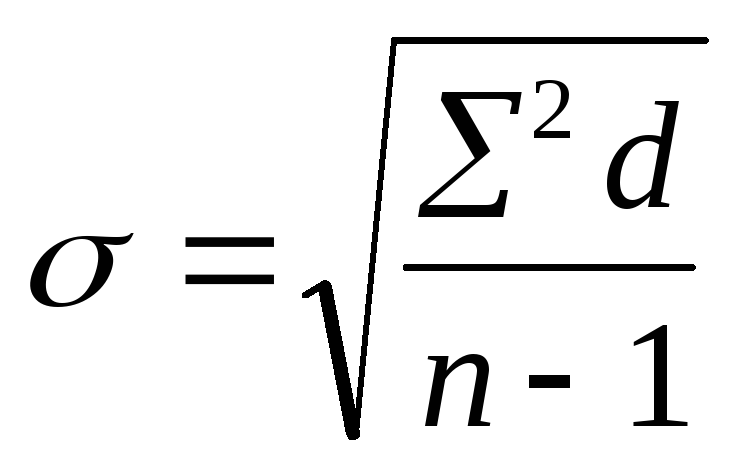Определяем среднюю величину по способу моментов

Вычисление средней арифметической по способу моментов

При большом числе наблюдений или при большом числовом значении вариант применяют

упрощенный способ вычисления средней арифметической- способ моментов.

где М — средняя арифметическая; А — условная средняя; i — интервал между группами вариант;

S — знак суммирования.; а- условное отклонение каждой варианты от условной средней;

р — частота встречаемости вариант; n — число наблюдений.

Пример вычисления средней арифметической по способу моментов (средней массы тела

юношей в возрасте 18 лет)

V(n в кг)	Р	а (V-А)	а . Р
+2	+4
+1	+3
Мо=62
-1	-6
-2	-8
-3	-3
п = 25	Sар = — 10кг

Этапы расчета средней по способу моментов:

1) за условную среднюю А рекомендуется принять Моду или Медиану, например А = 62кг, так как 62 кг было у 9 юношей из 25;

2) определяем «а» — условное отклонение варианты от условной средней, для этого из каждой варианты вычитаем условную среднюю: а = V — А, ( например, а = 64 — 62 = +2 и т.д.).

3) умножаем условное отклонение «а» на частоту «р» каждой варианты и получаем произведение а р;

4) находим сумму Sа . р = — 10кг

5) рассчитываем среднюю арифметическую по способу моментов:

М = А + i SаР = 62 — 1×0,4 = 61,6кг

Таким образом, можно сделать вывод, что в изучаемой нами группе юношей средняя масса тела

Средняя арифметическая сама по себе ничего не говорит о том вариационном ряде, из которого

она была вычислена. На ее типичность (достоверность) влияет однородность рассматриваемого

материала и колеблемость ряда.

Пример: даны два одинаковых по числу наблюдений вариационных ряда, в которых

представлены данные измерений окружности головы детей в возрасте от 1 года до 2-х лет

Ряд 1	Ряд 2
Окружность головы(в см) Частота	41, 45, 46, 47, 48 7, 8, 25, 6, 2	42, 43, 44, 45, 46, 47, 48, 49, 50 1, 2, 4, 6, 14, 10, 3, 0, 2

Имея одинаковое число наблюдений и одинаковые средние арифметические (М= 46 см), ряды

имеют различия в распределении внутри. Так варианты первого ряда отклоняются в целом от

средней арифметической с меньшим значением, чем варианты второго ряда, что дает

возможность предположить, что средняя арифметическая (46 см) более типична для первого

ряда, чем для второго.

В статистике для характеристики разнообразия вариационного ряда употребляют среднее

квадратическое отклонение (s)

Существует два способа расчета среднего квадратического отклонения: среднеарифметический

способ и способ моментов. При среднеарифметическом способе расчета применяют формулу:

где d истинное отклонение каждой варианты от истиной средней М. Формула используется при

Источник

Основные свойства средней величины:

1.имеется абстрактный характер так как является обобщающей величиной, в ней стираются

2.занимает срединное положение в ряду (в строго симметричном ряду)

3.сумма отклонений всех вариант от средней величины равна нулю. Данное свойство средней

величины используется для проверки правильности расчета средней величины.

Виды средних величин

1. Мода (Мо) — варианта, наиболее часто встречающая и в вариационном ряду.

2. Медиана (Ме) — варианта занимающая в вариационном ряду срединное

положение, т.е., центральная варианта, делящая вариационный ряд на две

3. Средняя арифметическая:

а).Средняя арифметическая простая

б).Средняя арифметическая взвешенная

в). Средняя арифметическая, вычисленная по способу моментов.

Вычисление средней арифметической , простой и взвешенной

В случаях, когда мы имеем простой вариационный ряд, в котором каждой варианте

соответствует частота (Р) равная 1, вычисляется средняя арифметическая простая по

формуле:

где М средняя арифметическая - знак суммирования V — варианта, n — число наблюдений

Таким образом, средняя арифметическая простая равна сумме всех вариант, деленной на число

Пример: Определение средней массы тела юношей в возрасте 18 лет (в кг)

Однако чаще всего приходится вычислять среднюю арифметическую взвешенную, которая

получается из взвешенных рядов, где каждая вариантавстречается различное количество раз

или, как говорят, имеет различный вес.

Средняя арифметическая взвешенная вычисляется по формуле:

n где М средняя арифметическая - знак суммирования , V — варианта,

Р -частота встречаемости, n — число наблюдений

Таким образом, средняя арифметическая взвешенная равна сумме произведений вариант на их

частоты, деленной на число всех наблюдений.

Пример: определение средней массы тела юношей в возрасте 18 лет (в кг.)

кг.

Вычисление средней арифметической по способу моментов

При большом числе наблюдений или при большом числовом значении вариант применяют

упрощенный способ вычисления средней арифметической- способ моментов.

где М — средняя арифметическая; А — условная средняя; i — интервал между группами вариант;

 — знак суммирования.; а- условное отклонение каждой варианты от условной средней;

р — частота встречаемости вариант; n — число наблюдений.

Пример вычисления средней арифметической по способу моментов (средней массы тела

юношей в возрасте 18 лет)

Этапы расчета средней по способу моментов:

1) за условную среднюю А рекомендуется принять Моду или Медиану, например А = 62кг, так как 62 кг было у 9 юношей из 25;

2) определяем «а» — условное отклонение варианты от условной средней, для этого из каждой варианты вычитаем условную среднюю: а = V — А, ( например, а = 64 — 62 = +2 и т.д.).

3) умножаем условное отклонение «а» на частоту «р» каждой варианты и получаем произведение а р;

4) находим сумму а . р = — 10кг

5) рассчитываем среднюю арифметическую по способу моментов:

М = А + i аР = 62 — 10,4 = 61,6кг

Таким образом, можно сделать вывод, что в изучаемой нами группе юношей средняя масса тела

Средняя арифметическая сама по себе ничего не говорит о том вариационном ряде, из которого

она была вычислена. На ее типичность (достоверность) влияет однородность рассматриваемого

материала и колеблемость ряда.

Пример: даны два одинаковых по числу наблюдений вариационных ряда, в которых

представлены данные измерений окружности головы детей в возрасте от 1 года до 2-х лет

Окружность головы(в см)

42, 43, 44, 45, 46, 47, 48, 49, 50

1, 2, 4, 6, 14, 10, 3, 0, 2

Имея одинаковое число наблюдений и одинаковые средние арифметические (М= 46 см), ряды

имеют различия в распределении внутри. Так варианты первого ряда отклоняются в целом от

средней арифметической с меньшим значением, чем варианты второго ряда, что дает

возможность предположить, что средняя арифметическая (46 см) более типична для первого

ряда, чем для второго.

В статистике для характеристики разнообразия вариационного ряда употребляют среднее

Существует два способа расчета среднего квадратического отклонения: среднеарифметический

способ и способ моментов. При среднеарифметическом способе расчета применяют формулу:

где d истинное отклонение каждой варианты от истиной средней М. Формула используется при

небольшом числе наблюдений (п 30)

Формула для определения по способу моментов:

где а — условное отклонение варианты от условной средней ;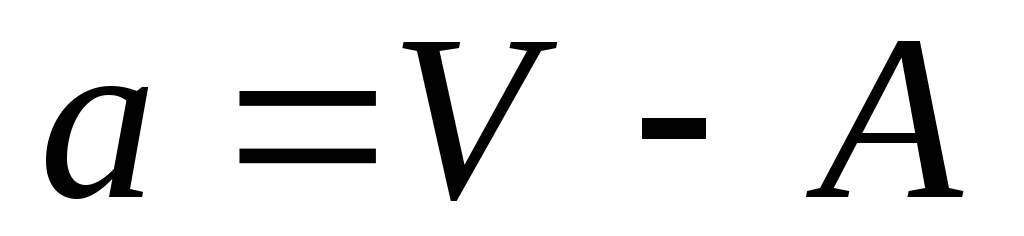

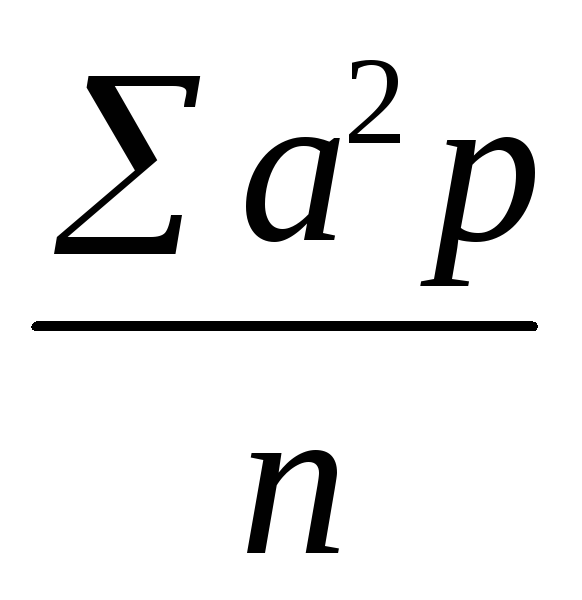
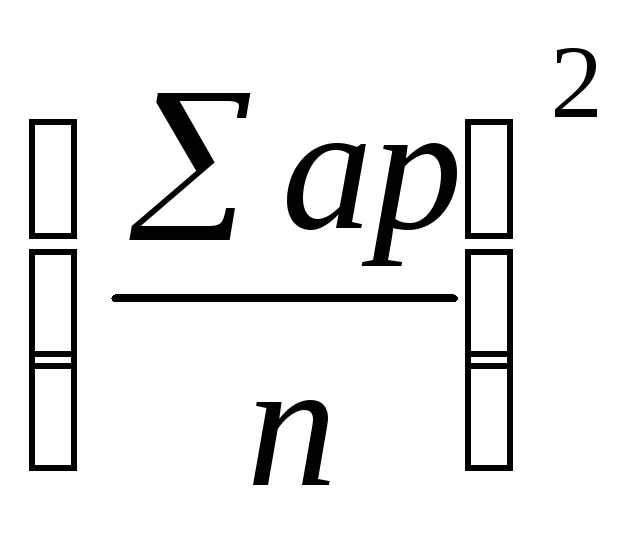
момент второй степени, а момент первой степени, возведенный в квадрат.

Теоретически и практически доказано, что если при большом числе наблюдений к средней

арифметической прибавить и отнять от нее 1(М1), то в пределах полученных величин

будет находится 68,3% всех вариант вариационного ряда. Если к средней арифметической

прибавить и отнять 2(М2), то в пределах полученных величин будет находиться 95,5%

всех вариант. М 3включает в себя 99,7% всех вариант вариационного ряда.

Исходя из этого положения можно проверить типичность средней арифметической для

вариационного ряда, из которого она была вычислена. Для этого надо к средней

арифметической прибавить и от нее отнять утроенную (М3). Если в полученные пределы

данный вариационный ряд укладывается, то средняя арифметическая типична, т.е. она

выражает основную закономерность ряда и ей можно пользоваться.

Указанное положение широко применяется при выработке различных стандартов (одежды,

обуви, школьной мебели и т.д).

Степень разнообразия признака в вариационном ряду можно оценить покоэффициенту

вариации(отношение среднего квадратического отклонения к средней арифметической,

умноженное на 100% )

При С_vменее 10% отмечается слабое разнообразие, при С_v10-20% — среднее, а при более 20% —

сильное разнообразие признака.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Решаем проверочные задачи по статистике

Тема: «Средние величины»

1. Задача на определение средней арифметической

Рассчитать средний возраст студентов в группе из 20 человек:

== 19,4 года

Если сгруппировать данные, то получим ряд распределения:

= = 19 , 4 года

2. Задача на нахождение средней арифметической взвешенной

Распределение рабочих по выработке деталей

Выработка деталей за смену одним рабочим, шт., Х _i

Число рабочих, fi

= = 19,4 деталей

3. Задача на в ычисление средней по групповым средним или по частным средним.

Распределение рабочих по среднему стажу работы

Средний стаж работы, лет.

Число рабочих, чел.,

==6,85 года

4. Задача на в ычисление средних в рядах распределения (интервальный ряд).

Распределение рабочих АО по уровню ежемесячной оплаты труда

Группы рабочих по оплате труда у.е.

Число рабочих, чел.

Середина интервала, х i

=(450*5+550*15+650*20+750*30+850*16+950*14)/100= 729 у.е.

Задача 5 . Вычисление средних в интервальных рядах методом моментов

Распределение малых предприятий региона по стоимости основных производственных фондов

Группы предприятий по стоимости ОПФ, у.е.

Для упрощения расчетов средней идут по пути уменьшения значений вариантов и частот.

Один из вариантов, обладающий наибольшей частотой принимают за А, i — величина интервала.

А- начало отсчета «способ отсчета от условного нуля», «способ моментов». Все варианты уменьшим на А, затем разделим на I , получим новый вариационный ряд распределения новых вариантов х _{i .} Средняя арифметическая их новых вариантов- момент первого порядка m _{i = = 0/25=0}

= m _I* I+ А =0*2+19=19 у . е .

Задача 6 на определение Средней гармонической.

Заработная плата предприятий АО

Численность промышленно- производственного персонала, чел

Месячный фонд заработной платы, тыс руб.

Средняя заработная плата, руб.

Определить среднюю з/п по всем предприятиям.

Составим логическую формулу средней: средняя з/п по всем предприятиям =

1) Пусть мы располагаем данными гр.1 и 2. Нам известен числитель и знаменатель логической формулы.

Искомая средняя величина определяется по средней агрегатной: _{= =}

2) Пусть мы располагаем данными гр.1 и 3 , нам известен числитель логической формулы, а знаменатель числитель не известен, но может быть найден путем умножения средней з/п на численность ППП. Искомая средняя определяется по средней арифметической взвешенной.

_{= =(1046*540+1210*275+1130*458)/1273=1112 руб.}

3) Пусть мы располагаем данными гр.2 и 3 , нам известен числитель логической формулы, а знаменатель не известен, но может быть найден путем деления фонда з/п на среднюю з/п логической формулы. Искомая средняя определяется по средней гармонической взвешенной:

Все ответы верны.

Задача 7. Определить среднюю цену моркови по всем магазинам.

Цена и выручка от реализации по трем коммерческим магазинам.

Цена моркови., руб за кг.

Выручка от реализации, руб.

Решение.

Логическая формула средней: средняя цена моркови =;

нам известен числитель логической формулы, а знаменатель не известен, но может быть найден путем деления выручки от реализации на цену моркови.

Искомая средняя определяется по средней гармонической взвешенной:

Задача 8 по статистике с решением: средние величины.

Информация о вкладах в банке

Число вкладов, тыс., f

Средний размер вклада, руб., x

Сумма вкладов, млн. руб., F

Средний размер вклада, x

Определить средний размер вклада по двум видам.

1) Пусть в октябре известен средний размер вкладов каждого вида и число вкладов. По формуле средней арифметической взвешенной:

_{= =}

2) Пусть в ноябре известен средний размер вкладов каждого вида и сумма вкладов. По формуле средней гармонической взвешенной:

Задача 9: Удельная материалоемкость по двум предприятиям, изготавливающим один и тот же вид продукции составила соответственно 2,5 и 3 кг. Вычислить среднюю удельную материалоемкость изделия по двум предприятиям при условии, что каждым предприятием израсходовано на изготовления одного изделия по 60 тонн стали.

1) Решение задачи по средней арифметической простой:

= = 2,75 кг/ед

2) решение по средней арифметической взвешенной

_{= =} 2,75 кг/ед

Оба решения не имеют логического смысла, чтобы правильно выбрать формулу средней величины необходимо составить логическую формулу задачи, отражающую ее смысл.

Логическая формула: средняя удельная материалоемкость по двум предприятиям = общему расходу материала на двух предприятиях/ на количество произведенных изделий→ средняя гармоническая взвешенная

3)

Источник