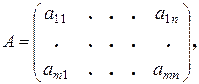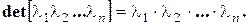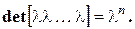Разложение определителей по элементам его рядов.
Всякий определитель равен сумме парных произведений элементов какого-либо ряда на их алгебраические дополнения.
;
или для j-го столбца:
Пример 7.1.Вычислить определитель разложением по элементам первой строки:
=1∙(1+12+12 
) 
∙(2+16+18 
)+
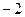
+3∙(4+8+27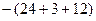 
) 
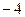
∙(8+4+18 
)=
=8 
= 
.
Теорема разложения позволяет заменить вычисление одного определителя n-го порядка вычислением n определителей (n-1)-го порядка.
Однако для упрощения вычислений целесообразно для определителей высоких порядков использовать метод «размножения нулей», основанный на свойстве 6 раздела 5. Его идея:
-сначала «размножить нули» в некотором ряду, т.е. получить ряд, в котором только один элемент не равен нулю, остальные нули;
-затем разложить определитель по элементам этого ряда.
Следовательно, на основании теоремы разложения исходный определитель равен произведению ненулевого элемента на его алгебраическое дополнение.
Пример7.2. Вычислить определитель:
.
«Размножим нули» в первом столбце.
От второй строки вычтем первую, умноженную на 2, от третьей строки вычтем первую, умноженную на 3, а от четвертой строки вычтем первую, умноженную на 4. При таких преобразованиях величина определителя не изменится.
По свойству 4 раздела 5 можем вынести 
за знак определителя из 1-го столбца, 
из 2-го столбца и 
из 3-го столбца.
Следствие: Определитель с нулевым рядом равен нулю.
2. Теорема замещения:
Сумма парных произведений каких-либо чисел на алгебраические дополнения некоторого ряда определителя равна тому определителю, который получается из данного, если в нем заменить элементы этого ряда взятыми числами.
Для 
-й строки:
1. Теорема аннулирования:
Сумма парных произведений элементов какого-либо ряда на алгебраические дополнения параллельного ряда равна нулю.
.
Действительно, по теореме замещения получаем определитель, у которого в k-й строке стоят те же элементы, что и в i-й строке
Но по свойству 3 раздела 5 такой определитель равен нулю.
Т.о., теорему разложения и ее следствия можно записать следующим образом:
8. Общие сведения о матрицах. Основные определения.
Определение 8.1 . Матрицей называется следующая прямоугольная таблица:
содержащая 
элементов 
,расположенных в т строках и в п столбцах.
Применяют также следующие обозначения матрицы: 
, или 
, или 
.
Строки и столбцы матрицы именуются рядами.
Величина 
называется размером матрицы.
Если в матрице поменять местами строки и столбцы, то получим матрицу, называемую транспонированной. Матрица, транспонированнаяс 
, обычно обозначается символом 
.
Например:
Определение 8.2. Две матрицы A и B называются равными, если
1) обе матрицы одинаковых размеров, т.е. 
и 
;
2) все их соответствующие элементы равны, т.е.
(8.1)
Тогда 
. (8.2)
Здесь одно матричное равенство (8.2) эквивалентно скалярных равенств (8.1).
9. Разновидности матриц.
1) Матрица, все элементы которой равны нулю, называется ноль-матрицей:
2) Если матрица состоит только из одной строки, то она называется матрицей-строкой, например 
. Аналогично этому матрица, имеющая только один столбец, именуется матрицей-столбцом, например 
.
Транспонирование переводит матрицу-столбец в матрицу-строку и наоборот.
3) Если m = n , то матрица называется квадратной матрицей n-го порядка.
Диагональ членов квадратной матрицы, идущая из левого верхнего угла в ее правый нижний угол, называется главной. Другая же диагональ ее членов, идущая из левого нижнего угла в ее правый верхний угол, именуется побочной.
Для квадратной матрицы может быть вычислен определитель det(A).
4) Если определитель матрицы равен нулю, то матрица называется особенной, или вырожденной. В противном случае матрица именуется неособенной, или невырожденной.
5) Разновидности квадратных матриц:
Если все элементы квадратной матрицы, за исключением элементов ее главной диагонали, равны нулю, то матрица называется диагональной. Диагональная матрица имеет вид: 
Ее определитель равен произведению элементов главной диагонали: 
В частности, при 
диагональная матрица называется скалярной: 
. 
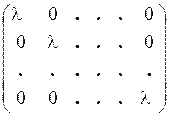
При 
скалярная матрица называется единичной и обозначается символом Е.
. Ее определитель равен единице: 
Если все элементы квадратной матрицы по одну сторону главной диагонали равны нулю, то матрица именуется треугольной (соответственно верхней или нижней).
— верхняя треугольная матрица.
Источник
Определитель матрицы: алгоритм и примеры вычисления определителя матрицы
Определитель (детерминант) матрицы — некоторое число, с которым можно сопоставить любую квадратную матрицу А = ( a i j ) n × n .
|А|, ∆ , det A — символы, которыми обозначают определитель матрицы.
Способ вычисления определителя выбирают в зависимости от порядка матрицы.
Определитель матрицы 2-го порядка вычисляют по формуле:
d e t A = 1 — 2 3 1 = 1 × 1 — 3 × ( — 2 ) = 1 + 6 = 7
Определитель матрицы 3-го порядка: правило треугольника
Чтобы найти определитель матрицы 3-го порядка, необходимо одно из правил:
- правило треугольника;
- правило Саррюса.
Как найти определитель матрицы 3-го порядка по методу треугольника?
а 11 а 12 а 13 а 21 а 22 а 23 а 31 а 32 а 33 = a 11 × a 22 × a 33 + a 31 × a 12 × a 23 + a 21 × a 32 × a 13 — a 31 × a 22 × a 13 — a 21 × a 12 × a 33 — a 11 × a 23 × a 32
А = 1 3 4 0 2 1 1 5 — 1
d e t A = 1 3 4 0 2 1 1 5 — 1 = 1 × 2 × ( — 2 ) + 1 × 3 × 1 + 4 × 0 × 5 — 1 × 2 × 4 — 0 × 3 × ( — 1 ) — 5 × 1 × 1 = ( — 2 ) + 3 + 0 — 8 — 0 — 5 = — 12
Правило Саррюса
Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:
- дописать слева от определителя два первых столбца;
- перемножить элементы, которые расположены на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
- перемножить элементы, которые расположены на побочных диагоналях и параллельных им, взяв произведения со знаком «—».
а 11 а 12 а 13 а 21 а 22 а 23 а 31 а 32 а 33 = a 11 × a 22 × a 33 + a 31 × a 12 × a 23 + a 21 × a 32 × a 13 — a 31 × a 22 × a 13 — a 21 × a 12 × a 33 — a 11 × a 23 × a 32
А = 1 3 4 0 2 1 — 2 5 — 1 1 3 0 2 — 2 5 = 1 × 2 × ( — 1 ) + 3 × 1 × ( — 2 ) + 4 × 0 × 5 — 4 × 2 × ( — 2 ) — 1 × 1 × 5 — 3 × 0 × ( — 1 ) = — 2 — 6 + 0 + 16 — 5 — 0 = 3
Методы разложения по элементам строки и столбца
Чтобы вычислить определитель матрицу 4-го порядка, можно воспользоваться одним из 2-х способов:
- разложением по элементам строки;
- разложением по элементам столбца.
Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.
Разложение матрицы по элементам строки:
d e t A = a i 1 × A i 1 + a i 2 × A i 2 + . . . + а i n × А i n
Разложение матрицы по элементам столбца:
d e t A = а 1 i × А 1 i + а 2 i × А 2 i + . . . + а n i × А n i
Если раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.
А = 0 1 — 1 3 2 1 0 0 — 2 4 5 1 3 2 1 0
- раскладываем по 2-ой строке:
А = 0 1 — 1 3 2 1 0 0 — 2 4 5 1 3 2 1 0 = 2 × ( — 1 ) 3 × 1 — 1 3 — 2 5 1 3 1 0 = — 2 × 1 — 1 3 4 5 1 2 1 0 + 1 × 0 — 1 3 — 2 5 1 3 1 0
- раскладываем по 4-му столбцу:
А = 0 1 — 1 3 2 1 0 0 — 2 4 5 1 3 2 1 0 = 3 × ( — 1 ) 5 × 2 1 0 — 2 4 5 3 2 1 + 1 × ( — 1 ) 7 × 0 1 — 1 2 1 0 3 2 1 = — 3 × 2 1 0 — 2 4 5 3 2 1 — 1 × 0 1 — 1 2 1 0 3 2 1
Свойства определителя
- если преобразовывать столбцы или строки незначительными действиями, то это не влияет на значение определителя;
- если поменять местами строки и столбцы, то знак поменяется на противоположный;
- определитель треугольной матрицы представляет собой произведение элементов, которые расположены на главной диагонали.
Пример 6
А = 1 3 4 0 2 1 0 0 5
d e t А = 1 3 4 0 2 1 0 0 5 = 1 × 5 × 2 = 10
Определитель матрицы, который содержит нулевой столбец, равняется нулю.
Источник
