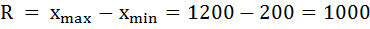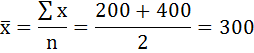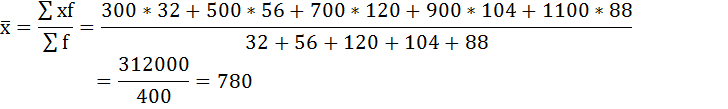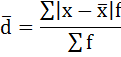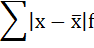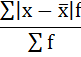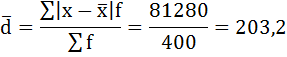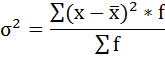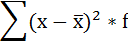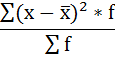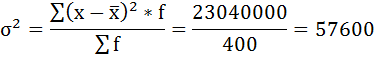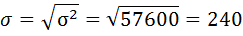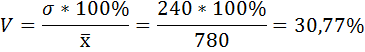Определите средний размер вклада используя способ моментов

Задача №6. Расчёт показателей вариации

По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:

Размер вклада, руб.	До 400	400 — 600	600 — 800	800 — 1000	Свыше 1000
Число вкладчиков	32	56	120	104	88

Определите:

1) размах вариации;

2) средний размер вклада;

3) среднее линейное отклонение;

5) среднее квадратическое отклонение;

6) коэффициент вариации вкладов.

Решение:

Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей.

Величина интервала второй группы равна 200, следовательно, и величина первой группы также равна 200. Величина интервала предпоследней группы равна 200, значит и последний интервал будет иметь величину, равную 200.

Размер вклада, руб.	200 — 400	400 — 600	600 — 800	800 — 1000	1000 — 1200
Число вкладчиков	32	56	120	104	88

1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:

Размах вариации размера вклада равен 1000 рублей.

2) Средний размер вклада определим по формуле средней арифметической взвешенной.

Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.

Среднее значение первого интервала будет равно:

второго — 500 и т. д.

Занесём результаты вычислений в таблицу:

Размер вклада, руб.	Число вкладчиков, f	Середина интервала, х	xf
200-400	32	300	9600
400-600	56	500	28000
600-800	120	700	84000
800-1000	104	900	93600
1000-1200	88	1100	96800
Итого	400	—	312000

Средний размер вклада в Сбербанке города будет равен 780 рублей:

3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:

Порядок расчёта среднего линейонго отклонения в интервальном ряду распределения следующий:

1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2).

2. Определяются абсолютные отклонения вариант от средней:

3. Полученные отклонения умножаются на частоты:

4. Находится сумма взвешенных отклонений без учёта знака:

5. Сумма взвешенных отклонений делится на сумму частот:

Удобно пользоваться таблицей расчётных данных:

Размер вклада, руб.	Число вкладчиков, f	Середина интервала, х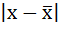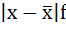
200-400	32	300	-480	480	15360
400-600	56	500	-280	280	15680
600-800	120	700	-80	80	9600
800-1000	104	900	120	120	12480
1000-1200	88	1100	320	320	28160
Итого	400	—	—	—	81280

Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля.

4) Дисперсия — это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.

Расчёт дисперсии в интервальных рядах распределения производится по формуле:

Порядок расчёта дисперсии в этом случае следующий:

1. Определяют среднюю арифметическую взвешенную, как показано в п. 2).

2. Находят отклонения вариант от средней:

3. Возводят в квадрат отклонения каждой варианты от средней:

4. Умножают квадраты отклонений на веса (частоты):

5. Суммируют полученные произведения:

6. Полученная сумма делится на сумму весов (частот):

Расчёты оформим в таблицу:

Размер вклада, руб.	Число вкладчиков, f	Середина интервала, х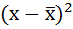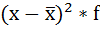
200-400	32	300	-480	230400	7372800
400-600	56	500	-280	78400	4390400
600-800	120	700	-80	6400	768000
800-1000	104	900	120	14400	1497600
1000-1200	88	1100	320	102400	9011200
Итого	400	—	—	—	23040000

5) Среднее квадратическое отклонение размера вклада определяется как корень квадратный из дисперсии:

6) Коэффициент вариации — это отношение среднего квадратического отклонения к средней арифметической:

По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.

Источник

Задача по статистике S-15

Номер задачи: S-15

Решение: бесплатно

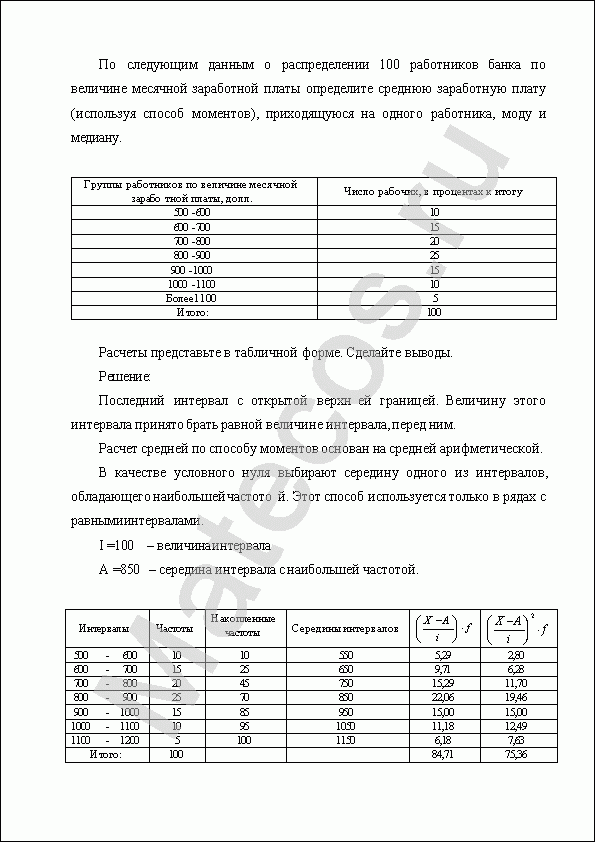
По следующим данным о распределении 100 работников банка по величине месячной заработной платы определите среднюю заработную плату (используя способ моментов), приходящуюся на одного работника, моду и медиану.

Группы работников по величине месячной заработной платы, долл.	Число рабочих, в процентах к итогу
500-600	10
600-700	15
700-800	20
800-900	25
900-1000	15
1000-1100	10
Более 1100	5
Итого:	100

Если Вы нашли, что искали, но решили набрать эту задачку самостоятельно, хочу немного облегчить Вам работу.

Ниже выкладываю «голый» текст задачи. Останется добавить формулы и графики.

По следующим данным о распределении 100 работников банка по величине месячной заработной платы определите среднюю заработную плату (используя способ моментов), приходящуюся на одного работника, моду и медиану.

Группы работников по величине месячной заработной платы, долл.

Число рабочих, в процентах к итогу

Расчеты представьте в табличной форме. Сделайте выводы.

Последний интервал с открытой верхней границей. Величину этого интервала принято брать равной величине интервала, перед ним.

Расчет средней по способу моментов основан на средней арифметической.

В качестве условного нуля выбирают середину одного из интервалов, обладающего наибольшей частотой. Этот способ используется только в рядах с равными интервалами.

I = 100 – величина интервала

A = 850 – середина интервала с наибольшей частотой.

m1 — момент первого порядка,

m2 — момент второго порядка.

Среднее квадратическое отклонение свидетельствует о том, что рассматриваемая величина в среднем отклоняется от средней величины на 18,97.

Вычислим моду и медиану:

Мода – наиболее часто встречающееся значение признака в совокупности.

Для интервального ряда распределения, сразу можно указать только интервал, где будут находиться мода и медиана.

Для определения их величины используют формулы:

Медианным называется интервал, которому соответствует значение накопленной частоты большей полусуммы всех частот.

Источник