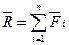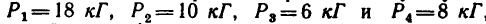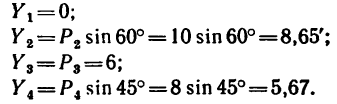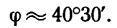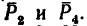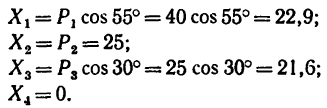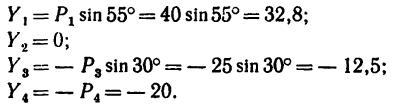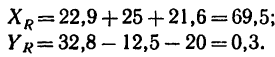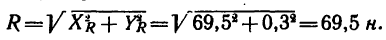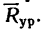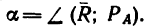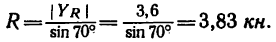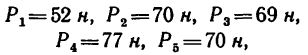Графический способ определения равнодействующей сходящихся сил на плоскости.
Пусть задана произвольная система сходящихся сил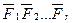 
, приложенных к твердому телу.
Перенесем эти силы как скользящие векторы в точку пересечения линий их действия. Затем, пользуясь аксиомой о параллелограмме сил, найдем равнодействующую этих сил. Равнодействующая такой системы может быть определена графически и аналитически.
Графически сложение двух сходящихся сил производится по правилу параллелограмма, причем 
. Затем по правилу параллелограмма складываем силы 
и 
, и получаем их равнодействующую 
. Продолжая процесс, получим 
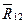
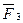
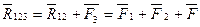
Процесс последовательного применения правила параллелограмма приводит к построению многоугольника из заданных сил. В силовом многоугольнике конец одной из сил служит началом другой. Равнодействующая сила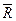 
в силовом многоугольнике соединяет начало первой силы с концом последней, т.е. изображается замыкающей силового многоугольника.
Для пространственной системы сходящихся сил силовой многоугольник является пространственной фигурой, для плоской — плоской.
Для равновесия системы сходящихся сил, приложенных к твердому телу, замыкающая силового многоугольника, изображающая равнодействующую силу, должна обратиться в точку, т. е. конец последней силы в многоугольнике должен совпадать с началом первой силы.
Такой силовой многоугольник называют замкнутым.
Получено условие равновесия системы сходящихся сил: для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая сила равнялась нулю 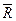= 0. Это условие является геометрическим.
Для случая трех сходящихся сил при равновесии должен быть замкнутым силовой треугольник, построенный из трех сил.
Источник
Равнодействующая сходящихся сил
Равнодействующая сходящихся сил
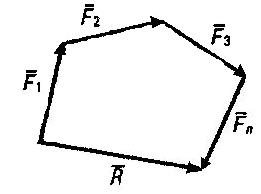
Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма или треугольника сил (4-я аксиома) (рис. 2.2).
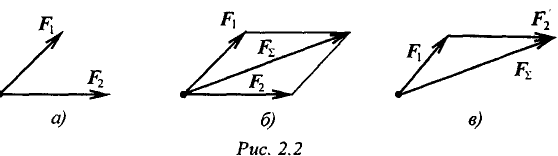
Используя свойства векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил (рис. 2.3). Вектор равнодействующей силы соединит начало первого вектора с концом последнего.
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называют геометрическим.
Замечание. При вычерчивании многоугольника обращать внимание на параллельность сторон многоугольника соответствующим векторам сил.
Эта теория взята со страницы решения задач по предмету «техническая механика»:
Возможно эти страницы вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Источник
Определение равнодействующей сходящихся сил в теоретической механике
Определение равнодействующей сходящихся сил:
Для сложения любого числа сходящихся сил применяется правило многоугольника. Используя это правило, задачу можно решить либо графическим методом либо методом проекций.
Задачи, решены методом проекций. Графическим методом рекомендуется решить эти задачи самостоятельно.
Задача №1
Определить равнодействующую четырех сил: 
Решение — методом проекций.
1. Изображаем на рисунке четыре данные силы и выбираем расположение осей проекций. В данном случае удобно начало осей поместить в точке А, а оси совместить с силами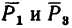 
(рис. 42, а).
2. Находим проекции данных сил на ось х: 
3. Находим проекции данных сил на ось у:
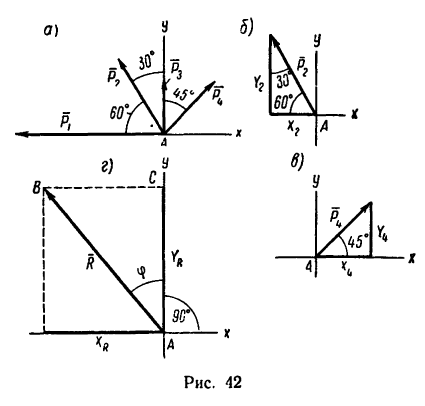
Если трудно определить знак и числовое значение проекции, то необходимо помнить, что проектируемую силу и две проекции на взаимно перпендикулярные оси всегда можно представить в виде прямоугольного треугольника. В тех случаях, когда еще нет достаточных навыков, силы и ее проекции можно изобразить отдельно, как показано на рис. 42,6 для силы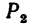 
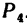
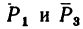
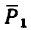
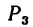
и на рис. 42, в для силы 
. Эти рисунки облегчают правильное определение проекций.
Для сил 
такие рисунки не нужны, так как сила 
лежит на оси х и, следовательно, проектируется на эту ось в натуральную величину, но зато на ось у проекция этой силы равна нулю. Сила 
проектируется в натуральную величину на ось у, а ее проекция на ось х равна нулю.
4. Находим проекции искомой равнодействующей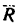 
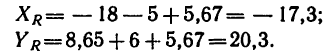
на оси хну:
Проекция на ось х получается отрицательной, а на ось у положительной. Значит вектор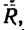 
заменяющий действие четырех данных сил и приложенный к точке А, должен быть направлен относительно оси у вверх, а относительно оси х — влево. Положение равнодействующей R показано отдельно на рис. 42, г.
5. Находим модуль равнодействующей (т. е. заканчиваем решение задачи первым путем, см. п. 7 в § 4-1):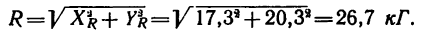 
6. Находим угол ф, определяющий направление R относительно оси у (см. рис. 42, а):
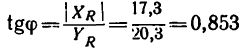
и, следовательно, 
Для определения угла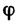 
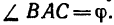
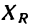
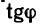
использован 
АВС (см. рис. 42, г), в котором 
Поэтому 
не имеет значения и в выражение 
подставлена его абсолютная величина.
Угол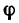 
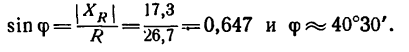
можно найти при помощи синуса:
Для определения угла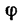 
можно воспользоваться и косинусом, но при работе с логарифмической счетной линейкой эта функция менее удобна.
Таким образом, равнодействующая четырех заданных сил равна 26,7 кГ направлена под углом 40°30′ к положительному направлению оси у и под углом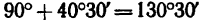 
к положительному направлению оси х.
Задача №2
К концу В веревки АВ прикреплено кольцо, на которое действуют четыре силы: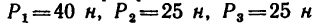 
, 
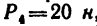
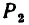
направленные, как показано на рис. 43, а (сила 
горизонтальна). Определить усилие, возникшее в веревке, и ее направление относительно горизонтали.
Решение — методом проекций.
1. Веревка будет натянута равнодействующей четырех заданных сил. Следовательно, определив модуль равнодействующей, получим усилие, возникшее в веревке, а определив направление равнодействующей, найдем положение натянутой веревки.
2. Изобразим точку В с действующими на нее силами на отдельном рисунке (рис. 43, 6) и совместим оси проекций с силами
3. Найдем проекции заданных сил на ось х:
4. Найдем проекции заданных сил на ось у:
5. Найдем проекции равнодействующей R на оси х и у:
6. Найдем модуль равнодействующей:
Как видно, в данном случае проекция равнодействующей на ось у очень мала по сравнению с проекцией на ось х. Поэтому равнодействующая практически численно равна проекции на ось х. Следовательно, можно принять, что вектор равнодействующей направлен вдоль оси х вправо (проекция на ось х положительна), т. е. горизонтально.
Таким образом, четыре заданные силы натягивают веревку равнодействующей силой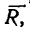 
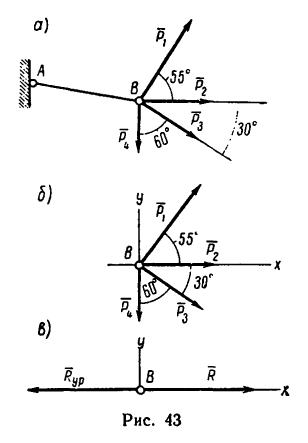
приложенной к точке В (к кольцу на конце веревки) и направленной горизонтально.
Другой конец веревки (точка А, рис. 43,а) закреплен, поэтому на кольцо В со стороны веревки действует еще одна сила, численно равная равнодействующей, но направленная в противоположную сторону. Эта сила называется уравновешивающей системы четырех сил.
На рис. 43, в показаны равнодействующая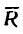 
и уравновешивающая 
Задача №3
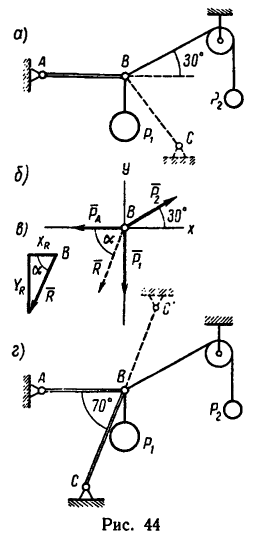
На конце В горизонтального стержня АВ необходимо прикрепить две нити с грузами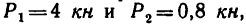 
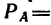
, как показано на рис. 44, а. Под каким углом к этому стержню следует присоединить второй стержень ВС, чтобы стержень АВ растягивался силой 
2 кн? Какое усилие при этом будет испытывать стержень ВС?
Соединения стержней между собой и с опорами шарнирные.
Решение — методом проекций.
1. На точку В действуют три силы: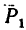 
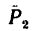
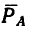
— вертикально вниз, 
— вдоль нити от точки В к блоку (под углом 30° к горизонтали) и противодействие (реакция) стержня 
тому растягивающему действию, которое испытывает стержень. Изобразим эти три силы на рис. 44,6 и найдем их равнодействующую, вдоль направления действия которой необходимо установить стержень ВС.
2. Оси проекций совместим с силами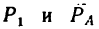 
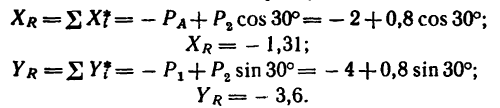
и определим проекции искомой равнодействующей сначала на ось х, а потом на ось у, зная, что каждая из них равна алгебраической сумме проекций данных сил на соответствующую ось:
3. Обе проекции получаются отрицательными. Значит равнодействующая расположится так, как показано штриховым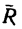 
на рис. 44,6, и положение стержня ВС определится углом 
4. Определим значение угла а из треугольника, образуемого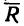 
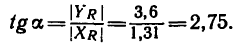
и его проекциями (рис. 44,в): 
Этому значению соответствует угол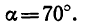
5. Стержень ВС необходимо установить под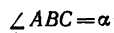
= 70° к стержню АВ., и тогда он будет сжиматься силой, равной
Описанное положение стержня показано на рис. 44, г.
Если же установить стержень, как показано на рисунке штриховой линией ВС, то стержень будет испытывать растяжение, равное той же силе R = 3,83 кн.
Задача №4
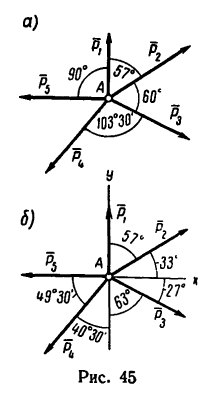
Определить равнодействующую пяти сил:
действующих на точку А, как показано на рис. 45,а.
Решение — методом проекций.
1. Так как силы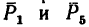 
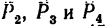
направлены друг к другу под прямым углом, то и совместим с этими силами ось проекций. Тогда векторы 
будут образовывать с осями проекций углы, показанные на рис. 45.б
2. Найдем проекцию равнодействующей на ось х:
* Здесь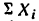 
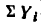
— обозначена алгебраическая сумма проекций всех сил на ось х, а 
— алгебраическая сумма проекций тех же сил на ось у.
3. Найдем проекцию равнодействующей на ось у:
4. Обе проекции искомой равнодействующей равны нулю, значит и сама равнодействующая также равна нулю.
Таким образом, данная система сил уравновешена. Иными словами, любую из пяти заданных сил можно рассматривать как уравновешивающую четыре остальных.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Равновесие сходящихся сил
- Равновесие трех непараллельных сил
- Сочлененные системы
- Равновесие пространственной системы сходящихся сил
- Потенциальная энергия
- Обобщенные координаты системы
- Сложение двух сил
- Разложение силы на две составляющие
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Источник
