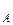Определите порядок реакции всеми возможными способами
Общий метод определения порядка реакции основан на законе действующих масс:
. (3.1)
Представим, что вещество B находится в большом избытке, и его концентрация мало меняется в ходе реакции. Тогда порядок реакции по веществу A можно определить, измерив скорость реакции при двух концентрациях A. Записывая уравнение (3.1) для двух моментов времени в логарифмической форме и вычитая одно выражение из другого, найдем порядок x:
.
В случае, если имеется больше двух экспериментальных точек, можно записать кинетические данные в координатах lnw — ln[A] и представить их в линейном виде с помощью метода наименьших квадратов. Тогда порядок реакции x будет равен тангенсу угла наклона прямой.
Если реакция имеет целый порядок, то для определения порядка используют различные частные методы. Метод подстановки заключается в том, что кинетические данные представляют в виде
где функция f соответствует решению кинетического уравнения для одного из целых порядков. Если величина k, определенная таким образом, будет постоянной, то мы угадали, т.е. выбрали верный порядок. Если k будет изменяться со временем, то надо выбрать функцию f, соответствующую другому порядку.
Другой способ определения целого порядка заключается в измерении зависимости времени протекания реакции от начальной концентрации. Из решения (2.1) кинетического уравнения для реакции n-го порядка следует, что время t x, за которое степень превращения достигнет x, обратно пропорционально (n-1)-й степени начальной концентрации (см. также (2.2)):
Измеряя время превращения t x при двух начальных концентрациях, можно определить порядок n по формуле:
.
Отметим, что разные начальные концентрации можно выбирать на одной и той же кинетической кривой.
Пример 3-1. В некоторой реакции целого порядка nA 
B концентрация исходного вещества 0.5 моль/л была достигнута за 4 мин при начальной концентрации 1 моль/л и за 5 мин при начальной концентрации 2 моль/л. Установите порядок реакции.
Решение. Из первого опыта следует, что период полураспада вещества при начальной концентрации 1 моль/л равен 4 мин. Во втором опыте при начальной концентрации 2 моль/л период полураспада равен 1 мин (от 2 моль/л до 0.5 моль/л — за 5 мин, из них от 1 моль/л до 0.5 моль/л — 4 мин, следовательно на превращение от 2 моль/л до 1 моль/л потребовалась 1 мин).
Таким образом, при увеличении начальной концентрации в 2 раза период полураспада уменьшился в 4 = 2 n-1 раза, следовательно порядок реакции n = 3.
Пример 3-2. Кинетика реакции первого порядка, в которой происходило образование кислоты, изучалась путем отбора проб реакционной смеси и их титрования одним и тем же раствором щелочи. Объемы щелочи, которые пошли на титрование:
Время, мин
Объем, мл
Докажите, что реакция имеет первый порядок. Рассчитайте период полураспада.
Решение. Запишем решение кинетического уравнения для реакции первого порядка в виде:
,
где a = x = 29.7 мл.
Время, мин
В течение реакции величина k остается постоянной, что и доказывает первый порядок.
Период полураспада равен
мин.
Пример 3-3. Реакция омыления метилацетата при 298 К описывается уравнением:
Для этой реакции получены следующие кинетические данные:
Время, мин
сNaOH, ммоль/л
Исходные концентрации щелочи и эфира одинаковы и равны 0.01 моль/л. Определите порядок реакции и константу скорости.
Решение. Запишем кинетические данные в координатах lnw-lnсNaOH, причем скорость реакции определим через конечные изменения концентраций и времени:
.
(Концентрацию вещества иногда обозначают не квадратными скобками, а буквой c). По этой приближенной формуле скорость лучше определять в середине временного интервала: t = (t1 + t2)/2. Концентрацию в этот момент времени определим как полусумму значений на границах интервала: c = (c1 + c2)/2. Сведем полученные данные в таблицу (учтем, что cNaOH = 10 ммоль/л при t = 0):
Источник
Методы определения порядка реакции
На практике исследование скорости химических реакций начинают с определения порядков этой реакции по каждому из реагирующих веществ и (или) порядка реакции в целом. Для реакции с участием нескольких веществ определить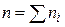 
можно только поэтапно, определяя порядки по отдельным веществам. Для этого используется метод избытка (метод изоляции, метод Оствальда), а затем определяют ni любым из описанных ниже методов.
Метод изоляции или метод избытка.
Если в исследуемой реакции участвуют несколько реагирующих веществ, то общий порядок реакции 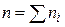, где ni — порядок по каждому из участников. Частный порядок ni можно определить, взяв все вещества, кроме данного, взять в большом избытке. Так, в случае реакции
.
Если вещества В и С взяты в большом избытке, то при протекании реакции их концентрации практически не изменяются, т.е.
.
.
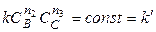
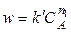
Тогда, определив порядки реакции по каждому из реагирующих веществ, можно найти общий порядок реакции:
Метод подстановки.
Этот метод заключается в том, что опытные результаты — текущие концентрации веществ в моменты времени t — последовательно подставляются в интегральные кинетические уравнения реакций нулевого (7), первого (9), второго (12 или 14) порядков и определяется, какое из уравнений дает практически постоянную величину константы скорости. Именно это уравнение и определяет порядок исследуемой реакции.
Графический вариант метода подстановки.
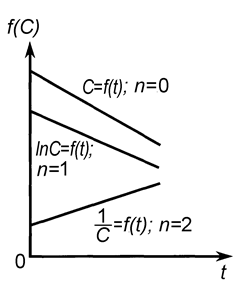
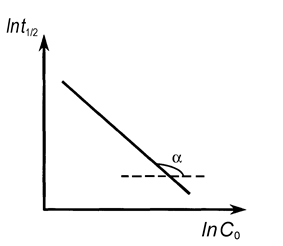
| Рис. 9. Линейные зависимости различных функций концентрации реагирующих веществ от времени. | Рис. 10. Определение порядка реакции по зависимости времени полупревращения от начальной концентрации |
Графический метод состоит в построении зависимостей различных функций концентрации от времени и определения, для какой из них наблюдается прямолинейная зависимость.
Линейные зависимости для реакций различных порядков получаются в следующих координатах (рис. 9): нулевого порядка С = f(t), первого порядка lnС = f(t), второго порядка 1/С = f(t).
Для реакций более высоких порядков выбираются координаты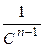 
—t.
Метод определения порядка реакции по времени полупревращения.
Порядок реакции определяется на основе опытной зависимости времен полупревращения (t1/2) от начальных концентраций веществ (C0).
Как уже отмечалось, для n = 0 время полупревращения прямо пропорционально величине С0, для n = 1 — не зависит от С0, а n = 2 — обратно пропорционально С0. Для реакции любого другого порядка справедливо соотношение (20)
, (20)
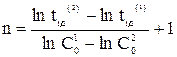
где t1/2 (1) и t1/2 (2) — время полупревращения при начальных концентрациях С01 и С02, соответственно.
Возможен графический вариант метода: по оси ординат откладываются значения ln(t1/2), а по оси абсцисс — значения lnC0 (рис. 10), тогда n = —tga + 1.
Дифференциальный метод Вант-Гоффа.
Этот метод применяют, когда в реакции участвует одно вещество, или при участии нескольких веществ, когда все вещества, кроме данного (А), взяты в большом избытке. Тогда скорость реакции равна
. (21)
Прологарифмируем уравнение (21):
lnw = lnk + n lnС
Очевидно, что в координатах lnw- lnC мы получим линейную зависимость, причем n = tga.
Построив зависимость lnw от lnC (рис. 11), можно определить порядок реакции, равный в данном случае тангенсу угла наклона прямой (n = tga).
Рис. 11. Определение порядка реакции дифференциальным методом Вант-Гоффа.
Источник
Определите порядок реакции всеми возможными способами
Общий метод определения порядка реакции основан на законе действующих масс:
. (3.1)
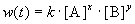
Представим, что вещество B находится в большом избытке, и его концентрация мало меняется в ходе реакции. Тогда порядок реакции по веществу A можно определить, измерив скорость реакции при двух концентрациях A. Записывая уравнение (3.1) для двух моментов времени в логарифмической форме и вычитая одно выражение из другого, найдем порядок x:
.
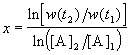
В случае, если имеется больше двух экспериментальных точек, можно записать кинетические данные в координатах lnw — ln[A] и представить их в линейном виде с помощью метода наименьших квадратов. Тогда порядок реакции x будет равен тангенсу угла наклона прямой.
Если реакция имеет целый порядок, то для определения порядка используют различные частные методы. Метод подстановки заключается в том, что кинетические данные представляют в виде
где функция f соответствует решению кинетического уравнения для одного из целых порядков. Если величина k, определенная таким образом, будет постоянной, то мы угадали, т.е. выбрали верный порядок. Если k будет изменяться со временем, то надо выбрать функцию f, соответствующую другому порядку.
Другой способ определения целого порядка заключается в измерении зависимости времени протекания реакции от начальной концентрации. Из решения (2.1) кинетического уравнения для реакции n-го порядка следует, что время t x, за которое степень превращения достигнет x, обратно пропорционально (n-1)-й степени начальной концентрации (см. также (2.2)):
Измеряя время превращения t x при двух начальных концентрациях, можно определить порядок n по формуле:
.
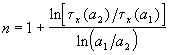
Отметим, что разные начальные концентрации можно выбирать на одной и той же кинетической кривой.
Пример 3-1. В некоторой реакции целого порядка nA 
B концентрация исходного вещества 0.5 моль/л была достигнута за 4 мин при начальной концентрации 1 моль/л и за 5 мин при начальной концентрации 2 моль/л. Установите порядок реакции.
Решение. Из первого опыта следует, что период полураспада вещества при начальной концентрации 1 моль/л равен 4 мин. Во втором опыте при начальной концентрации 2 моль/л период полураспада равен 1 мин (от 2 моль/л до 0.5 моль/л — за 5 мин, из них от 1 моль/л до 0.5 моль/л — 4 мин, следовательно на превращение от 2 моль/л до 1 моль/л потребовалась 1 мин).
Таким образом, при увеличении начальной концентрации в 2 раза период полураспада уменьшился в 4 = 2 n-1 раза, следовательно порядок реакции n = 3.
Пример 3-2. Кинетика реакции первого порядка, в которой происходило образование кислоты, изучалась путем отбора проб реакционной смеси и их титрования одним и тем же раствором щелочи. Объемы щелочи, которые пошли на титрование:
Время, мин
Объем, мл
Докажите, что реакция имеет первый порядок. Рассчитайте период полураспада.
Решение. Запишем решение кинетического уравнения для реакции первого порядка в виде:
,
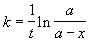
где a = x = 29.7 мл.
Время, мин
В течение реакции величина k остается постоянной, что и доказывает первый порядок.
Период полураспада равен
мин.
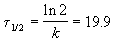
Пример 3-3. Реакция омыления метилацетата при 298 К описывается уравнением:
Для этой реакции получены следующие кинетические данные:
Время, мин
сNaOH, ммоль/л
Исходные концентрации щелочи и эфира одинаковы и равны 0.01 моль/л. Определите порядок реакции и константу скорости.
Решение. Запишем кинетические данные в координатах lnw-lnсNaOH, причем скорость реакции определим через конечные изменения концентраций и времени:
.
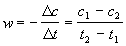
(Концентрацию вещества иногда обозначают не квадратными скобками, а буквой c). По этой приближенной формуле скорость лучше определять в середине временного интервала: t = (t1 + t2)/2. Концентрацию в этот момент времени определим как полусумму значений на границах интервала: c = (c1 + c2)/2. Сведем полученные данные в таблицу (учтем, что cNaOH = 10 ммоль/л при t = 0):
Источник
