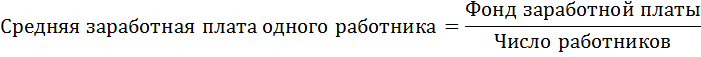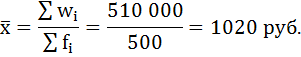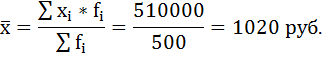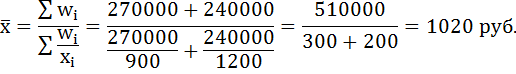Задача №4. Расчёт средней заработной платы
Имеются следующие данные об оплате труда работников малых предприятий:
| № предприятия | Фонд заработной платы, руб. | Среднесписочная численность работников, руб. | Среднемесячная заработная плата, руб. | Удельный вес работников, % |
|---|---|---|---|---|
| А | 1 | 2 | 3 | 4 |
| 1 | 270 000 | 300 | 900 | 60 |
| 2 | 240 000 | 200 | 1200 | 40 |
Определите среднюю заработную плату работников предприятий, используя показатели:
Решение:
Для определения средней заработной платы воспользуемся следующим соотношением:
а) Используя показатели 1 и 2 графы, построим новую таблицу исходных и расчётных данных:
| № предприятия | Фонд заработной платы, руб., wi | Среднесписочная численность работников, руб., fi |
|---|---|---|
| А | 1 | 2 |
| 1 | 270 000 | 300 |
| 2 | 240 000 | 200 |
| Итого: | 510 000 | 500 |
Итоги 1 и 2 графы содержат необходимые величины для расчёта искомой средней. Воспользуемся формулой средней агрегатной:
wi = xifi;
xi – i-й вариант осредняемого признака;
f i – вес i-го варианта.
б) Если мы располагаем только показателями 2 и 3 графы, таблица исходных и расчётных данных будет следующая:
| № предприятия | Среднесписочная численность работников, руб., fi | Среднемесячная заработная плата, руб., xi | xi fi |
|---|---|---|---|
| А | 2 | 3 | 4 |
| 1 | 300 | 900 | 270 000 |
| 2 | 200 | 1200 | 240 000 |
| Итого: | 500 | — | 510 000 |
Нам известен знаменатель исходного соотношения средней, но не известен его числитель. Однако фонд заработной платы можно получить, умножив среднемесячную заработную плату на среднесписочную численность работников (гр. 4 последней таблицы). Поэтому общая средняя может быть рассчитана по формуле средней арифметической взвешенной:
в) Теперь используем только показатели 1 и 3 графы:
| № предприятия | Фонд заработной платы, руб., wi | Среднемесячная заработная плата, руб., xi |
|---|---|---|
| А | 1 | 3 |
| 1 | 270 000 | 900 |
| 2 | 240 000 | 1200 |
| Итого: | 510 000 | — |
То есть известен теперь числитель в формуле расчёта средней заработной платы, но не известен знаменатель. Число работников по каждому предприятию можно получить делением фонда заработной платы на среднемесячную заработную плату. Тогда расчёт средней заработной платы в целом по двум предприятиям будет произведён по формуле средней гармонической взвешенной:
г) Теперь известны только показатели гр.3 и 4:
| № предприятия | Среднемесячная заработная плата, руб., xi | Удельный вес работников, %, fi |
|---|---|---|
| А | 3 | 4 |
| 1 | 900 | 60 |
| 2 | 1200 | 40 |
| Итого: | — | 100 |
Данная задача аналогична задаче б) с той только разницей, что роль численности работников в данном случае выполняет её доля в общем итоге, выраженная в процентах. Для расчёта воспользуемся средней арифметической взвешенной:
Следовательно, среднюю заработную плату работников предприятий в зависимости от исходных данных можно рассчитать и по формуле средней арифметической, и средней гармонической, и средней агрегатной. Но выбор конкретной формы средней зависит от экономического смысла изучаемого показателя – от его исходного соотношения. Поэтому при решении подобной задачи вначале следует составить исходное соотношение средней, что поможет определиться с необходимой формулой.
Источник
Решаем проверочные задачи по статистике
Тема: «Средние величины»
1. Задача на определение средней арифметической
Рассчитать средний возраст студентов в группе из 20 человек:
=
= 19,4 года
Если сгруппировать данные, то получим ряд распределения:
= 
= 19 , 4 года
2. Задача на нахождение средней арифметической взвешенной
Распределение рабочих по выработке деталей
Выработка деталей за смену одним рабочим, шт., Х i
Число рабочих, fi
= = 19,4 деталей
3. Задача на в ычисление средней по групповым средним или по частным средним.
Распределение рабочих по среднему стажу работы
Средний стаж работы, лет. 
Число рабочих, чел.,
=
=6,85 года
4. Задача на в ычисление средних в рядах распределения (интервальный ряд).
Распределение рабочих АО по уровню ежемесячной оплаты труда
Группы рабочих по оплате труда у.е.
Число рабочих, чел.
Середина интервала, х i
=(450*5+550*15+650*20+750*30+850*16+950*14)/100= 729 у.е.
Задача 5 . Вычисление средних в интервальных рядах методом моментов
Распределение малых предприятий региона по стоимости основных производственных фондов
Группы предприятий по стоимости ОПФ, у.е.
Для упрощения расчетов средней идут по пути уменьшения значений вариантов и частот.
Один из вариантов, обладающий наибольшей частотой принимают за А, i — величина интервала.
А- начало отсчета «способ отсчета от условного нуля», «способ моментов». Все варианты уменьшим на А, затем разделим на I , получим новый вариационный ряд распределения новых вариантов х i . Средняя арифметическая их новых вариантов- момент первого порядка m i = 
= 0/25=0
= m I* I+ А =0*2+19=19 у . е .
Задача 6 на определение Средней гармонической.
Заработная плата предприятий АО
Численность промышленно- производственного персонала, чел
Месячный фонд заработной платы, тыс руб.
Средняя заработная плата, руб.
Определить среднюю з/п по всем предприятиям.
Составим логическую формулу средней: средняя з/п по всем предприятиям = 
1) Пусть мы располагаем данными гр.1 и 2. Нам известен числитель и знаменатель логической формулы.
Искомая средняя величина определяется по средней агрегатной: = 
= 
2) Пусть мы располагаем данными гр.1 и 3 , нам известен числитель логической формулы, а знаменатель числитель не известен, но может быть найден путем умножения средней з/п на численность ППП. Искомая средняя определяется по средней арифметической взвешенной.
= 
=(1046*540+1210*275+1130*458)/1273=1112 руб.
3) Пусть мы располагаем данными гр.2 и 3 , нам известен числитель логической формулы, а знаменатель не известен, но может быть найден путем деления фонда з/п на среднюю з/п логической формулы. Искомая средняя определяется по средней гармонической взвешенной:
Все ответы верны.
Задача 7. Определить среднюю цену моркови по всем магазинам.
Цена и выручка от реализации по трем коммерческим магазинам.
Цена моркови., руб за кг.
Выручка от реализации, руб.
Решение.
Логическая формула средней: средняя цена моркови =
;
нам известен числитель логической формулы, а знаменатель не известен, но может быть найден путем деления выручки от реализации на цену моркови.
Искомая средняя определяется по средней гармонической взвешенной:
Задача 8 по статистике с решением: средние величины.
Информация о вкладах в банке
Число вкладов, тыс., f
Средний размер вклада, руб., x
Сумма вкладов, млн. руб., F
Средний размер вклада, x
Определить средний размер вклада по двум видам.
1) Пусть в октябре известен средний размер вкладов каждого вида и число вкладов. По формуле средней арифметической взвешенной:
= = 
2) Пусть в ноябре известен средний размер вкладов каждого вида и сумма вкладов. По формуле средней гармонической взвешенной:
Задача 9: Удельная материалоемкость по двум предприятиям, изготавливающим один и тот же вид продукции составила соответственно 2,5 и 3 кг. Вычислить среднюю удельную материалоемкость изделия по двум предприятиям при условии, что каждым предприятием израсходовано на изготовления одного изделия по 60 тонн стали.
1) Решение задачи по средней арифметической простой:
= 
= 2,75 кг/ед
2) решение по средней арифметической взвешенной
= = 
2,75 кг/ед
Оба решения не имеют логического смысла, чтобы правильно выбрать формулу средней величины необходимо составить логическую формулу задачи, отражающую ее смысл.
Логическая формула: средняя удельная материалоемкость по двум предприятиям = общему расходу материала на двух предприятиях/ на количество произведенных изделий→ средняя гармоническая взвешенная
3) 
Источник
