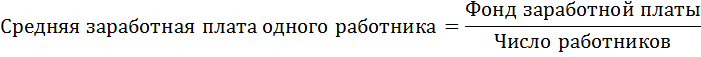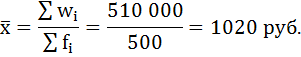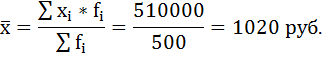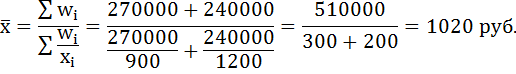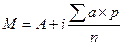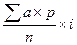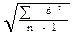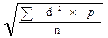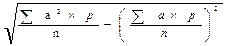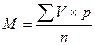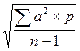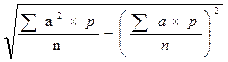Задача №4. Расчёт средней заработной платы
Имеются следующие данные об оплате труда работников малых предприятий:
| № предприятия | Фонд заработной платы, руб. | Среднесписочная численность работников, руб. | Среднемесячная заработная плата, руб. | Удельный вес работников, % |
|---|---|---|---|---|
| А | 1 | 2 | 3 | 4 |
| 1 | 270 000 | 300 | 900 | 60 |
| 2 | 240 000 | 200 | 1200 | 40 |
Определите среднюю заработную плату работников предприятий, используя показатели:
Решение:
Для определения средней заработной платы воспользуемся следующим соотношением:
а) Используя показатели 1 и 2 графы, построим новую таблицу исходных и расчётных данных:
| № предприятия | Фонд заработной платы, руб., wi | Среднесписочная численность работников, руб., fi |
|---|---|---|
| А | 1 | 2 |
| 1 | 270 000 | 300 |
| 2 | 240 000 | 200 |
| Итого: | 510 000 | 500 |
Итоги 1 и 2 графы содержат необходимые величины для расчёта искомой средней. Воспользуемся формулой средней агрегатной:
wi = xifi;
xi – i-й вариант осредняемого признака;
f i – вес i-го варианта.
б) Если мы располагаем только показателями 2 и 3 графы, таблица исходных и расчётных данных будет следующая:
| № предприятия | Среднесписочная численность работников, руб., fi | Среднемесячная заработная плата, руб., xi | xi fi |
|---|---|---|---|
| А | 2 | 3 | 4 |
| 1 | 300 | 900 | 270 000 |
| 2 | 200 | 1200 | 240 000 |
| Итого: | 500 | — | 510 000 |
Нам известен знаменатель исходного соотношения средней, но не известен его числитель. Однако фонд заработной платы можно получить, умножив среднемесячную заработную плату на среднесписочную численность работников (гр. 4 последней таблицы). Поэтому общая средняя может быть рассчитана по формуле средней арифметической взвешенной:
в) Теперь используем только показатели 1 и 3 графы:
| № предприятия | Фонд заработной платы, руб., wi | Среднемесячная заработная плата, руб., xi |
|---|---|---|
| А | 1 | 3 |
| 1 | 270 000 | 900 |
| 2 | 240 000 | 1200 |
| Итого: | 510 000 | — |
То есть известен теперь числитель в формуле расчёта средней заработной платы, но не известен знаменатель. Число работников по каждому предприятию можно получить делением фонда заработной платы на среднемесячную заработную плату. Тогда расчёт средней заработной платы в целом по двум предприятиям будет произведён по формуле средней гармонической взвешенной:
г) Теперь известны только показатели гр.3 и 4:
| № предприятия | Среднемесячная заработная плата, руб., xi | Удельный вес работников, %, fi |
|---|---|---|
| А | 3 | 4 |
| 1 | 900 | 60 |
| 2 | 1200 | 40 |
| Итого: | — | 100 |
Данная задача аналогична задаче б) с той только разницей, что роль численности работников в данном случае выполняет её доля в общем итоге, выраженная в процентах. Для расчёта воспользуемся средней арифметической взвешенной:
Следовательно, среднюю заработную плату работников предприятий в зависимости от исходных данных можно рассчитать и по формуле средней арифметической, и средней гармонической, и средней агрегатной. Но выбор конкретной формы средней зависит от экономического смысла изучаемого показателя – от его исходного соотношения. Поэтому при решении подобной задачи вначале следует составить исходное соотношение средней, что поможет определиться с необходимой формулой.
Источник
Способ моментов
Применяя этот способ, среднюю арифметическую рассчитывают по формуле: 
Эта формула технически упрощает расчеты, особенно в тех случаях, когда варианты состоят из многозначных чисел, а совокупность — из большого числа наблюдений.
Например: Методика расчета средней арифметической величины по способу моментов Таблица 8.
| V кг | p | а | а ×р |
| 64 | 2 | +2 | +4 |
| 63 | 3 | +1 | +3 |
| 62 | 9 | 0 | 0 |
| 61 | 6 | -1 | -6 |
| 60 | 4 | -2 | -8 |
| 59 | 1 | -3 | -3 |
| n =25 | Sа × р = -10 кг |
Этапы расчета М по способу моментов:
1) за условную среднюю Ао рекомендуется принять варианту, чаще других повторяющуюся в вариационном ряду. В нашем примере: Ао = М = 62 кг., так как 62 кг было у 9 юношей из 25;
2) определяем а — условное отклонение от условной средней. Для этого из каждой варианты вычитаем условную среднюю а = (V — Ао).
В нашем примере: а = 64 — 62 = + 2 и т. д.;
3) умножаем условное отклонение (а) на частоту (р) каждой варианты и получаем произведения
(а × р).
В нашем примере: 2 ×(+2) = 4 и т.д.
4) получаем сумму S а × р
В нашем примере: — 10кг;
5) определяем интервал между группами вариант ( I)
В нашем примере: i = 1 кг;
6) момент первой степени 
В нашем примере: -10 кг / 25× 1 = — 0,4
7)рассчитываем среднюю арифметическую по способу моментов:
В нашем примере: М = 62 кг – 0,4 = 61,6 кг
Есливариационный ряд предварительно был сгруппирован, то в качестве ряда(V)используются середины групп.
Средняя арифметическая величина обладает тремя свойствами.
1. Средняя занимает серединное положение в вариационном ряду. В строго симметричном ряду: М = Мо = Ме.
2. Средняя является обобщающей величиной и за ней не видны колебания, различия индивидуальных данных.
3. Сумма отклонений всех вариант от средней равна нулю. Sd = S (V-M) = 0
Величина того или иного признака неодинакова у всех членов совокупности, несмотря на ее относительную однородность.
Наиболее полную характеристику разнообразию признака в совокупности дает так называемое среднее квадратическое отклонение, обозначаемое греческой буквой «сигма» — s.
Существует два способа расчета среднего квадратического отклонения: среднеарифметический и способ моментов. При среднеарифметическом способе расчета применяют формулу: s = 
где d— истинное отклонение вариант от истинной средней (V-М). Эта формула используется при небольшом числе наблюдений (n 1 используют формулу такого вида:
s =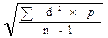 
;
При Р>1 и N>30 — s = 
Следующая формула предназначена для определения s по способу моментов: s =i× 
где а — условное отклонение вариант от условной средней: а =V — А; Sa 2 ×p/n момент второй степени, а (Sa×p/n) 2 — момент первой степени, возведённый в квадрат. Этот способ применяется в тех случаях, когда нет вычислительной техники, а вариационный ряд громоздкий как за счет большого числа наблюдений, так и за счет вариант, выраженных многозначными числами. При числе наблюдений, равном 30 и менее, в моменте второй степени n заменяют на (n-1).
Например: Расчет среднего квадратического отклонения по среднеарифметическому способу. Таблица 9.
| Рост мальчиков 12 лет. | Число детей (р) | V • Р | d | d 2 | d 2 × Р |
| 155 | 1 | 155 | +2 | 4 | 4 |
| 154 | 4 | 616 | +1 | 1 | 4 |
| 153 | 6 | 918 | 0 | 0 | 0 |
| 152 | 4 | 608 | —1 | 1 | 4 |
| 151 | 1 | 151 | —2 | 4 | 4 |
| М = 153 | n = 16 | SV ×p = 1448 | S d 2 × Р = 16 |
Последовательность расчета s.
1.Определить М (по среднеарифметическому способу). 
В нашем примере: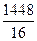 
= 153см.
2.Найти истинное отклонение d =(V-M).
В нашем примере:155-153=+2; 154-153= +1 и т.д.
3.Возвести каждое отклонение в квадрат d 2.
4.Найти произведение (d 2 × р) по всем строкам ряда.
5.Определить сумму (S d 2 ×р).
В нашем примере: 4+4+0+4+4=16
6.Рассчитать s по формуле: 
В нашем примере: Ö16/16-1 =1,05 см.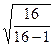 
=1,05
Например: Расчет среднего квадратического отклоненияпо способу моментов Таблица 10.
| Рост, см (V) | Число детей (р) | а | а×р а×р | a 2 ×р |
| 155 | 1 | +2 | 2 | 4 |
| 154 | 4 | + 1 | 4 | 4 |
| 153 | 6 | 0 | 0 | 0 |
| 152 | 4 | -1 | -4 | 4 |
| 151 | 1 | -2 | -2 | 4 |
| n = 16 | Sар = 0 | Sa 2 ×р = 16 |
Последовательность расчета s по способу моментов.
1.Найти условную среднюю А
В нашем примере: А =153 cм.
2.Определить условное отклонение (а) каждой варианты от условной средней: а =V — А.
3.Получить произведения а × р, а затем их просуммировать.
В нашем примере: =0.
4.Рассчитать истинную среднюю арифметическую по формуле
=153 см, так как сумма отклонений равна 0, то поэтому М=А.
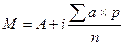
5.Получить произведения а 2 ×p по всем строкам вариационного ряда и просуммировать их.
В нашем примере:Sa 2 ×p =16.
6. Рассчитать по способу моментов по формуле: s =i× 
В нашем примере:s =1×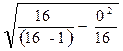 
= 1,05
Ошибка репрезентативности (m) является важнейшей статистической величиной, необходимой для оценки достоверности результатов исследования. Эта ошибка возникает в тех случаях, когда требуется по части охарактеризовать явление в целом. Эти ошибки неизбежны. Они проистекают из сущности выборочного исследования: генеральная совокупность может быть охарактеризована по выборочной совокупности только с некоторой погрешностью, измеряемой ошибкой репрезентативности.
По величине ошибки репрезентативности определяют, насколько результаты, полученные при выборочном наблюдении, отличаются от результатов, которые могли бы быть получены при проведении сплошного исследования всех без исключения элементов генеральной совокупности.
Ошибки репрезентативности можно свести к достаточно малой величине, т. е. к величине допустимой погрешности. Делается это путем привлечения в выборку достаточного количества наблюдений (n):
· 
– для выборочного исследования, в котором будут рассчитываться относительные величины.
· 
– для выборочного исследования, в котором будут рассчитываться средние величины.
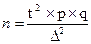
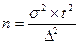
p– вероятность наступления явления (выбирается по данным аналогичных исследований)
q— вероятность не наступления явления, q =100-p
t— доверительный критерий – таблица 11.
D— предельная ошибка, вытекает из таблицы 6, исходя из выбранного t.
| Степень безошибочного прогноза (Р) | Доверительный критерий (t) | Предельная ошибка (D) |
| 68% | — | |
| 95% | 5% | |
| 99% | 1% |
Если аналогичных исследований нет, то p и q принимаются как 50% на 50%.
Ошибки репрезентативности рассчитываются по следующим формулам:
· 
– для относительных величин;
· 
– для средних величин.
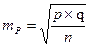
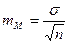
В медицине и здравоохранении по разности параметров оценивают средние и относительные величины, полученные для разных групп населения по полу, возрасту, а также групп больных и здоровых и т. д. Во всех случаях при сопоставлении двух сравниваемых величин возникает необходимость не только определить их разность, но и оценить ее достоверность. Достоверность разности величин, полученных при выборочных исследованиях, означает, что вывод об их различии может быть перенесен на соответствующие генеральные совокупности. Достоверность различия сравниваемых величин измеряется доверительным критерием (критерием точности t), который рассчитывается по специальным формулам для средних и относительных величин.
Формула оценки достоверности разности сравниваемых величин такова:
· 
— для средних величин;
· 
— для относительных величин.
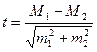
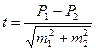
Разность величин считается достоверной при значениях, равных или больших 2. Р1 всегда выбирается больше, чем Р2.
Например: При изучении влияния анаболических гормонов при инфаркте миокарда на белковый обмен были получены следующие данные: общий белок до лечения (Р) составил 7,14% (m-±0,17%), после лечения (Р) 8,04% (m-±0,12%).
1. Определяем большую величину как Р1, а меньшую как Р2.
2.Возводим ошибки репрезентативности в квадраты:
В нашем примере: 0,17 2 =0,0289;0,12 2 = 0,0144.
3.Складываем квадраты и извлекаем квадратный корень.
В нашем примере: Ö0,0289+0,0144=Ö0,0433 = 0,2.
4.Находим разность сравниваемых величин и делим на знаменатель.
В нашем примере:8,04-7,14=0,9/0,2=4,5.
В нашем примере: 4,5>2, значит разность величин достоверна, т.е, анаболические гормоны действительно увеличивают уровень общего белка.
Источник
