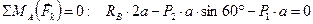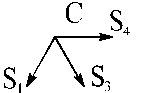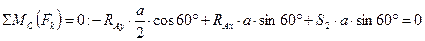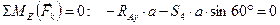Определить сил стержня способы вырезания узлов

Метод вырезания узлов

Способы расчета ферм

1. Метод вырезания узлов (аналитический и графический).

2. Метод Риттера (метод сечений).

3. Диаграмма Максвелла-Кремоны.

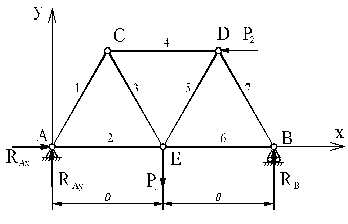
1. Предварительно определяем силы опорных реакций, рассматривая равновесие фермы в целом.

Составим систему уравнений равновесия фермы:

,

,

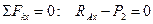
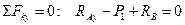
Отсюда найдем опорные реакции:

, , .

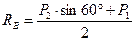
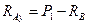
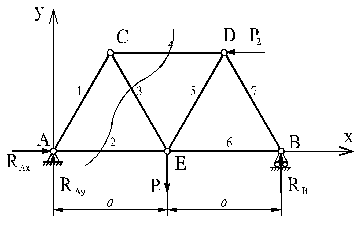
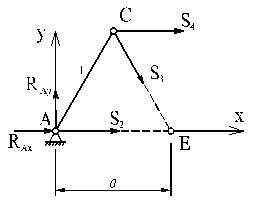
2. Теперь переходим к определению усилий в стержнях. Для сокращения записей пронумеруем стержни согласно рисунку.

При вырезании условимся направлять силы реакций в стрежнях фермы (усилия в стержнях) от узлов, предполагая, что все стержни растянуты. Если в результате решения задачи величина усилия окажется положительной, то предположение о растяжении будет подтверждено, а если величина усилия отрицательна, то стержень фактически испытывает сжатие.

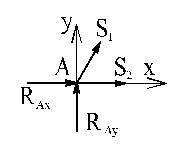
Решение задачи методом вырезания узлов можно начинать только с тех узлов, в которых сходится по два неизвестных усилия. Вырезаем узел А. Выбрав направление декартовых осей, составляем систему уравнений равновесия узла А.

,

,

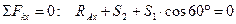
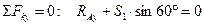
Решив эту систему, находим S₁ и S₂.

Теперь можно перейти к узлу С, так как после определения усилия S₁ в этом узле осталось только две неизвестные силы: S₄ и S₃. Составляем и решаем систему уравнений равновесия узла С.

,

,

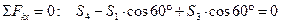
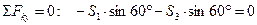
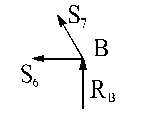
Теперь рассматриваем равновесие узла В.

,

,

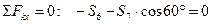
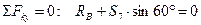
находим из этих уравнений S₆ и S₇.

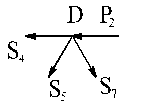
Остается определить усилие S₅. Для этого можно рассмотреть равновесие узла D либо Е. Рассмотрим равновесие узла D. Запишем уравнения равновесия узла D в проекциях на декартовы оси.

,

,

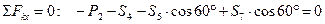
Для определения S₅ достаточно одного из этих уравнений – второго.

Первое уравнение системы можно использовать для проверки полученных результатов.
Метод Риттера

1. Определяем опорные реакции, рассматривая равновесие фермы в целом (см. метод вырезания узлов).

2. Мысленно разрезаем ферму на две части, так, чтобы число рассеченных стержней не превышало трех, отбрасываем одну из частей и заменяем действие отброшенной части искомыми усилиями в стержнях, полагая все стержни растянутыми.

3. Составляем уравнения равновесия для оставшейся части таким образом, чтобы в каждое уравнение входило только одно неизвестное усилие. Для этого составляем уравнения моментов относительно точек, в которых пересекаются линии действия неизвестных усилий. Если два стрежня параллельны, то составляем уравнение проекций на ось, перпендикулярную к этим стержням.

,

4. Решая каждое из составленных уравнений, находим искомое усилие в стержнях. Если в ответе получим знак минус, то это означает, что стержень сжат, а не растянут.

Источник

Расчет усилий в стержнях фермы

Содержание:

Расчет ферм состоит в определении продольных усилий в стержнях, а также перемещений отдельных узлов. Настоящий параграф посвящен определению усилий в стержнях ферм. Для нахождения внутренних усилий мысленно разрезают ферму на две части и рассматривают условия равновесия одной из частей, к которой прикладывают внешние силы и пока неизвестные усилия в разрезанных стержнях.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Расчет усилий в стержнях фермы

Фермой называется конструкция, состоящая из стержней, соединённых между собой шарнирами, которые называются узлами фермы. Внешняя нагрузка на ферму передаётся через эти узлы. Каждый стержень в ферме находится в условиях простого осевого растяжения – сжатия, но общая деформация фермы – изгибная, то есть ферма работает на изгиб.

Простые фермы

Фермой называется геометрически неизменная конструкция, состоящая из стержней, соединенных между собой на концах шарнирами (рис.6.1).

Шарниры, соединяющие стержни между собой, называются узлами фермы. Стержни, расположенные внутри контура фермы, образуют ее решетку. Если все стержни, образующие ферму, расположены в одной плоскости, то такая ферма называется плоской.

При расчете ферм принимается, что весом стержней можно пренебречь и шарниры расположены на концах стержней. Поскольку нагрузки, действующие на ферму, передаются в шарнирах, то каждый стержень будет воспринимать усилие, которое направлено вдоль оси стержня, то есть будет либо растянут или сжат.

Среди разнообразных типов ферм различают два основных вида:

1. фермы без лишних стержней.

2. фермы, в которых есть лишние стержни.

В дальнейшем будем рассматривать простые плоские фермы, которые строятся следующим образом: к основному стержневому треугольнику двумя стержнями присоединяется новый шарнир (узел), к него второй и т.д.

По своему назначению фермы подразделяются в основном на мостовые, стропильные и крановые (рис.6.1 а, б, в).

Зависимость между числом стержней и числом узлов для фермы без лишних стержней имеет вид:

Если , то число стержней является недостаточным для обеспечения геометрической неизменности фермы. Если же , то ферма имеет лишние стержни.

При расчете ферм предполагается, что выполняются следующие условия:

1. все стержни фермы — прямолинейные.

2. трение в шарнирах отсутствует.

3. силы, действующие на ферму, лежат в плоскости этой фермы и приложены только к ее узлам.

4. собственный вес каждого стержня фермы настолько мал по сравнению с силами приложенными к узлам фермы, что им можно пренебречь.

Основной задачей расчета простых ферм является определение усилий в стержнях фермы, которые представляют собой внутренние силы, возникающие в стержнях под действием внешних сил.

Определение усилий в стержнях фермы

Ограничимся двумя аналитическими способами определения усилий в стержнях простых ферм:

1. способ вырезания узлов.

2. способ сечений (метод Риттера).

Способ вырезания узлов состоит в том, что каждый узел вырезают из фермы и рассматривают отдельно в равновесии под действием приложенных к нему внешних сил и усилий разрезанных стержней.

Метод Риттера позволяет определить усилия в любом стержне фермы независимо от усилий в других стержнях и заключается в том, что ферма рассекается на две части таким образом, чтобы в сечении было не более трех стержней с неизвестными усилиями.

Определения усилий в стержнях фермы

Определение усилий в стержнях ферм упрощается, если при рассмотрении равновесия узла встречаются следующие случаи.

1. Узел фермы с двумя стержнями без нагрузка (рис.6.2).

В этом случае усилия в каждом из стержней равны нулю, поскольку иначе равновесие узла было бы невозможно.

2. Узел фермы с двумя стержнями, по оси одного из которых приложена сила (рис.6.3).

Реакция стержня, с осью которого совпадает направление силы, по модулю равна, а по направлению противоположна силе . Усилие же во втором стержне равно нулю.

3. Узел фермы с тремя стержнями, оси двух стержней которого направлены вдоль прямой (рис.6.4).

В этом случае усилие в третьем стержне равно нулю, а в каждом из первых двух или тоже равны нулю, либо равны между собой по величине и направлены в противоположные стороны, то есть эти стержни либо не подвергаются нагрузкам, либо оба сжаты (растянуты) с одинаковыми силами.

4. Узел фермы с тремя стержнями, у которого оси двух стержней направлены вдоль одной прямой, а по направлению оси третьего стержня приложена сила (рис.6.5).

В этом случае реакция третьего стержня по величине равна, а по направлению противоположна силе . Усилия в первых двух стержнях либо равны нулю, либо равны между собой по величине и направлены в противоположные стороны.

5. К узлу фермы с тремя стержнями с осью одного из стержней приложена сила , а усилие в одном из двух других стержней равно нулю (рис.6.6).

В этом случае реакция стержня, ось которого совпадает с линией действия силы , по величине равна, а по направлению противоположна силе .Усилия во втором и третьем стержнях равны нулю.

6. Узел фермы с четырьмя стержнями, в которой оси стержней попарно расположены по одной прямой (рис.6.7).

В этом случае усилия или:

а) равны нулю в каждом стержне;
б) равны нулю только в двух стержнях, что расположены по одной прямой, а в двух других равны по модулю и противоположны по направлению;
в) для каждой пары стержней, что расположены по одной прямой, равны между собой по модулю и противоположны по направлению.

Порядок решения задач на тему: Расчет усилий в стержнях фермы

Существует два способа:

Способ вырезания узлов

1. Выделить ферму, равновесие которой надо рассмотреть для нахождения неизвестных величин.

2. Приложить активные силы, действующие на объект равновесия.

3. Отбросить связи и заменить их действие реакциями.

4. Рассмотреть равновесие фермы, как твердого тела, под действием активных сил и реакций связей.

5. Определить реакции опор.

6. Вырезать узел, к которому сходятся два стержня и рассмотреть его равновесие под действием активных сил и реакций разрезанных стержней. (При выборе направления реакции стержня, лучше принимать что он растянут, то есть направлять реакцию от узла стержня).

7. Пользуясь условиями равновесия плоской системы сходящихся сил, определить реакции разрезанных стержней.

8. Двигаясь по ферме от узла к узлу, аналогично рассматривается равновесие каждого узла. При этом, в каждом последующем вырезанном узле должно быть только два стержня, реакции в которых неизвестны.

Способ сечений (метод Риттера)

1. Определить опорные реакции, рассматривая равновесие фермы как твердого тела, находящегося под действием плоской системы сил.

2. Мысленно разрезать ферму, к которой приложены все внешние силы, на две части таким образом, чтобы число разрезанных стержней не было больше трех.

3. Отбросить одну из частей фермы и заменить ее действие реакциями разрезанных стержней. (Рекомендуется принимать, что все стержни растянуты).

4. Рассмотреть равновесие выбранной части фермы под действием активных сил и реакций разрезанных стержней. (При составлении условий равновесия лучше руководствоваться тем, чтобы в каждое уравнение входила одна неизвестная реакция. Для этого, за центр моментов выбирают точку, где пересекаются линии действия двух неизвестных реакций, а в случае, когда два разрезанных стержня параллельны, составляют уравнение проекций на ось, которая перпендикулярна этим стержням).

5. Решить составленную систему уравнений, определить неизвестные усилия в стержнях.

Примеры решения задач на тему: Расчет усилий в стержнях фермы

Ферма (рис.6.8) нагружена вертикальными силами , , и .

Определить опорные реакции и усилия в стержнях, если

Решим задачу первым способом – методом вырезания узлов.

Для определения опорных реакций рассмотрим равновесие фермы в целом.

На ферму действуют активные силы , , и и реакции опор и .

Свяжем с фермой систему координат : ось направим горизонтально через опоры и ; ось – вертикально вверх.

Реакция шарнирно-подвижной опоры направлена перпендикулярно опорной поверхности, то есть вертикально. Поскольку все активные силы и реакция перпендикулярны оси , то и реакция шарнирно-неподвижной опоры тоже будет перпендикулярна оси .

Составим уравнения равновесия для системы сил, действующей на ферму:

где

Из второго уравнения получим :

Из первого уравнения найдем :

После определения реакций опор перейдем к определению усилий в стержнях. Для этого надо рассмотреть равновесие каждого узла фермы в отдельности, мнимо отбросив все сходящиеся к нему стержни и заменив их действие на узел реакциями.

Первыми надо рассматривать узлы, к которым приложены только две неведомые силы. В данной задаче таким требованиям соответствуют два узла и . Расчет можно начинать с любого из этих узлов.

Начнем с узла . Узел находится в равновесии под действием реакции , активной силы и неизвестных реакций и стержней 1 и 5 (рис.6.9).

Реакции стержней направим от узла, предполагая, что стержни растянуты.

Через точку проводим оси и и составляем уравнения равновесия плоской системы сходящихся сил:

Решив последовательно уравнения (4) и (3), получим:

Отрицательное значение реакции указывает на то, что действительное ее направление в противоположную показанному на рис.6.9. Стержень 5 не растянут, а сжат. Стержень 1 — растянут.

Следующим рассмотрим узел , поскольку к узлу надо будет приложить три неизвестных реакции и , а к узлу — только две — и , усилие в стержне 5 этого узла уже определено.

Узел находится в равновесии под действием: активной силы ; известной реакции , которая по величине равна реакции , приложенной к узлу , но направлена в противоположную сторону; неизвестных реакций и стержней 4 и 6 (рис.6.10).

Проведем через точку оси координат и составим уравнения равновесия узла:

Из уравнения (5) выразим :

Подставим выражение для в (6) и найдем :

Таким образом, стержень 6 растянут, как и предполагалось, а стержень 4 – сжат.

Следующим вырезаем узел .

К узлу приложены две неизвестные реакции и стержней 7 и 2; две известные реакции , и , стержней 6 и 1, которые за величинами равны реакциям и , приложенным соответственно к узлам и , но направлены в противоположные стороны (рис.6.11).

Проводим через точку координатные оси и составляем уравнения равновесия узла :

Из уравнения (8) найдем

Из уравнения (7) находим :

Таким образом, стержень 2 растянут, а стержень 7 – сжат.

Рассмотрим равновесие узла (рис.6.12).

На узел действуют неизвестна реакция стержня 3; активная сила ; известна реакция стержня 4, которая по модулю равна реакции , приложенной к узлу , но противоположно направлена; известна реакция стержня 7, которая по модулю равна реакции , что приложена к узлу , но противоположно направлена.

Через точку проводим оси координат и . Поскольку на узел действует только одна неизвестная сила , то достаточно составить только одно уравнение равновесия:

Стержень 3 — сжатый.

Таким образом определены усилия во всех стержнях фермы. Выяснено, что стержни 1, 2, 6 – растянуты, а стержни 3, 4, 5 и 7 – сжаты.

Рассмотрение равновесия узла (рис.6.13), позволяет проверить правильность расчета фермы.

Уравнения равновесия для узла :

Подставив в эти уравнения числовые данные, получим:

Уравнения (10) и (11) преобразуются в тождества, что указывает на правильность выполненного расчета.

Проверим, насколько верно определены усилия в отдельных стержнях фермы методом сечений (методом Риттера).

Для определения усилий в стержнях 1, 6, 4 рассечем ферму сечением на две части таким образом, чтобы в сечение попало не более трех стержней, усилия в которых неизвестны (рис.6.14). Отбросим правую часть фермы, заменив ее действие реакциями стержней и . Реакции стержней направим от узлов и , представив, что все стержни растянуты (рис.6.15).

Таким образом, левая часть фермы будет находиться в равновесии под действием реакции опоры , активных сил , и реакций стержней , .

Составим уравнения равновесия для левой части фермы.

Воспользуемся формой условий равновесия в виде 3-х уравнений моментов для произвольной плоской системы сил.

Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех сил относительно трех произвольных центров, которые не лежат на одной прямой, были равны нулю:

Выберем за центры моментов точки:

, где пересекаются линии действия неизвестных реакций и ;

, где пересекаются линии действия неизвестных реакций и ;

, где пересекаются линии действия неизвестных реакций и .

Из уравнения (12) определим реакцию :

где — плечо сил и относительно центра ;

— плечо реакции относительно центра ,

Из уравнения (13) определим:

где — плечо сил и относительно центра ;

— плечо силы относительно центра ,

— плечо реакции относительно центра ,

Из уравнения (14) найдем:

где — плечо сил и относительно центра ,

— плечо реакции относительно центра ,

Таким образом, при определении усилий в стержнях фермы методом сечений, имеем что полностью совпадает с результатами, которые найдены методом вырезания узлов.

Ответ:

Услуги по теоретической механике:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник