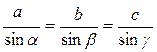Определение равнодействующей системы сил аналитическим способом
Практическая работа 1
Тема: Определение реакций связей аналитическим и графическим способами.
Цель: Изучить виды связей, научиться определять их реакции.
Теоретическая часть:
Тело, которое не скреплено с другими телами и может совершать из данного положения любые перемещения в пространстве, называется свободным.
Тело, перемещениям которого в пространстве препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным.
Все то, что ограничивает перемещения данного тела в пространстве, называется связью.
Сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям, называется силой реакции связи или реакцией связи.
Реакция связи направлена в сторону, противоположную той, куда связь не дает перемещаться телу.
Аксиома связей. Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями этих связей.
Все виды связей можно разделить на несколько типов.
1. Связь – гладкая опора (без трения).
Реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре (рисунок 1.1).
2. Гибкая связь (нить, веревка, трос, цепь).
Реакция нити направлена вдоль нить от тела, при этом нить может быть только растянута (рисунок 1.2).
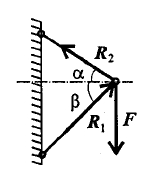
3. Жесткий стержень.
Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи (рисунок 1.3).
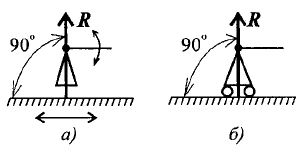
4. Шарнирная опора.
Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.
Подвижный шарнир. Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, т.к. не допускается только перемещение поперек опорной поверхности
Неподвижный шарнир. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Её принято изображать в виде двух составляющих: горизонтальной и вертикальной (рисунок 1.5).
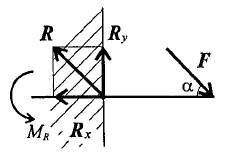
5. Защемление или «заделка».
Любые перемещения точки крепления невозможны.
Реактивную силу принято представлять в виде двух составляющих вдоль осей координат (рисунок 1.6).
Пример.
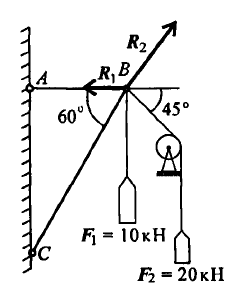
Грузы подвешены на стержнях и канатах и находятся в равновесии. Определить реакции стержней АВ и СВ (рисунок 1.7).
1. Аналитический способ.
1. Определяем вероятные направления реакций. Мысленно убираем стержень АВ, при этом стержень СВ опускается, следовательно, точка В отодвигается от стены: назначение стержня АВ – тянуть точку В к стене.
Если убрать стержень СВ, точка В опустится, следовательно, стержень СВ поддерживает точку В снизу – реакция направлена в верх.
2. Освобождаем точку В от связи.
3. Выберем направление осей координат, ось Ох совпадает с реакцией 
4. Запишем уравнения равновесия точки В:
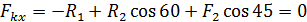

5. Из второго уравнения получаем:
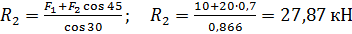
Из первого уравнения получаем:
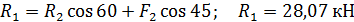
2. Графический способ.
1. Выбираем масштабный коэффициент сил: µ = 1 Н/мм
Определяем отрезки, изображающие силы 
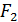
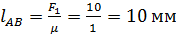
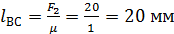
2. Полученная система сил находится в равновесии, поэтому силовой
многоугольник должен быть замкнутым (рисунок 1.8).
3. Вычисляем реакции 
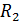
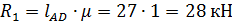


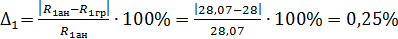
Задание.
Аналитически и графически определить реакции связей, сравнить результаты.
Контрольные вопросы.
1. Что называется связью?
2. Перечислите основные виды опор.
3. Запишите аксиому связей.
4. Как направлена реакция гибкой нити?
Содержание отчета
1. Схема фигуры в масштабе
3. Ответы на контрольные вопросы
Практическая работа № 2
Тема:Определение реакций опор двух опорной балки.
Цель работы:Научится определять реакции опор балки установленной на двух опорах.
Теоретическая часть:
Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца вектора (рис. 3.1).

Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси. Таким образом, проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси (рис. 3.2).
Проекция силы на две взаимно перпендикулярные оси (рис. 3.3).
Определение равнодействующей системы сил аналитическим способом
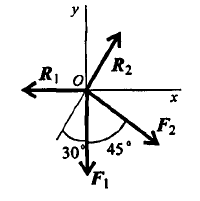
Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определяем равнодействующую геометрическим способом.
Выберем систему координат, определим пропорции всех заданных векторов на эти оси (рис. 3.4, а).
Складываем проекции всех векторов на оси х и у (рис. 3.4, б).

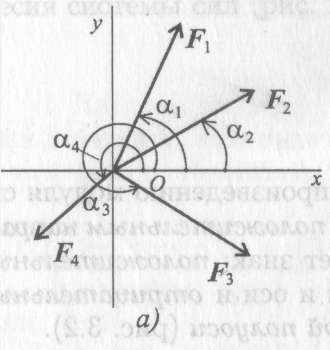
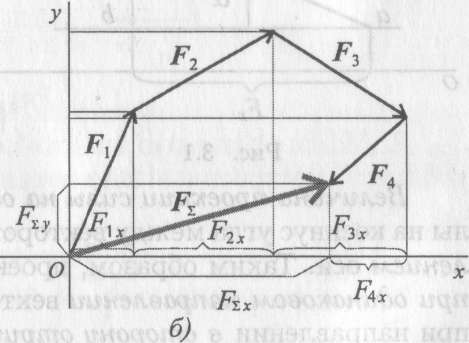
| Рис. 3.4 |
Модуль (величину) равнодействующей можно найти по известным проекциям:

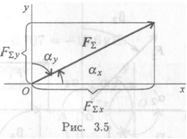
Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующей с осями координат (рис. 3.5).
Источник
Решение задач на равновесие геометрическим способом
Геометрическим способом удобно пользоваться, если в системе три силы. При решении задач на равновесие тело считать абсолютно твердым (отвердевшим).
Порядок решения задач:
1. Определить возможное направление реакций связей.
2. Вычертить многоугольник сил системы, начиная с известных сил в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура.)
3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
4. Для уточнения решения рекомендуется определить величины, векторов (сторон многоугольника) с помощью геометрических зависимостей.
Пример 1. Груз подвешен на стержнях и находится в равновесии. Определить усилия в стержнях (рис. 2.5, а).

1. Усилия, возникающие в стержнях крепления, по величине равны силам, с которыми стержни поддерживают груз (5-я аксиома статики) (рис. 2.5, а).
Определяем возможные направления реакций связей «жесткие стержни».
. γ = 180 0 – 60 0 – 45 0
Усилия направлены вдоль стержней.
2. Освободим точку А от связей, заменив действие связей их реакциями (рис. 2.5, б).
3. Система находится в равновесии. Построим треугольник сил. Построение начнем с известной силы, вычертив вектор F в некотором масштабе.
Из концов вектора F проводим линии, параллельные реакциям и R1 и R2.
Пересекаясь, линии создадут треугольник (рис. 2.5, в). Зная масштаб построений и измерив длину сторон треугольника, можно определить величину реакций в стержнях.
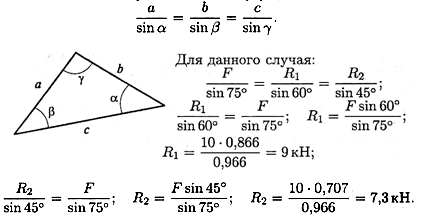 |
4. Для более точных расчетов можно воспользоваться геометрическими соотношениями, в частности теоремой синусов: отношение стороны треугольника к синусу противоположного угла — величина постоянная:
Замечание. Если направление вектора (реакции связи) на заданной схеме и в треугольнике сил не совпало, значит, реакция на схеме должна быть направлена в противоположную сторону.
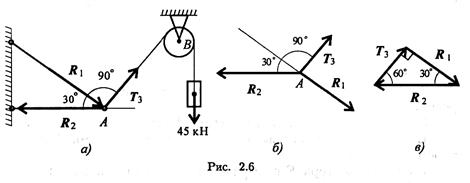
Пример 2. Груз подвешен на стержнях и канатах и находится в равновесии. Определить усилия в стержнях (рис. 2.6, а).
 |
Решение
1. Нанесем на схему возможные направления усилий, приложенных в точке А. Реакции стержней — вдоль стержней, усилие от каната — вдоль каната от точки А к точке В.
2. Груз находится в равновесии, следовательно, в равновесии находится точка А, в которой пересекаются три силы.
Освободим точку А от связей и рассмотрим ее равновесие (рис. 2.6, б).
Замечание. Рассмотрим только силы, приложенные к точке А. Груз растягивает канат силой 45 кН по всей длине, поэтому усилие от каната известно: Тз = 45 кН.
3. Строим треугольник для сил, приложенных в точке А, начиная с известной силы Т3. Стороны треугольника параллельны предполагаемым направлениям сил, приложенных в точке А.
Образовался прямоугольный треугольник (рис. 2.6, е).
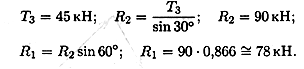 |
4. Неизвестные реакции стержней можно определить из соотношений в прямоугольном треугольнике:
Замечание. При равновесии векторы сил в треугольнике направлены один за другим (обходим треугольник по часовой стрелке). Сравним направления сил в треугольнике с принятыми в начале расчета на рис. 2.6, а. Направления совпали, следовательно, направления реакций определены верно.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Решение задач на равновесие геометрическим способом
Геометрическим способом удобно пользоваться, если в системе три силы. При решении задач на равновесие тело считать абсолютно твердым (отвердевшим).
Порядок решения задач:
1. Определить возможное направление реакций связей.
2. Вычертить многоугольник сил системы, начиная с известных сил в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура.)
3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
4. Для уточнения решения рекомендуется определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.
Решение задач на равновесие плоской системы
Сходящихся сил аналитическим методом
Непосредственное применение условий равновесия в геометрической форме дает наиболее простое решение для системы трех сходящихся сил. При наличии в системе четырех и более сил рациональнее применять аналитический метод, который является универсальным и применяется чаще всего. При аналитическом методе решение этих задач выполняется на основе уравнений равновесия по следующему плану:
первый этап — выделяют объект равновесия тело или точку, где пересекаются линии действия всех сил, т. е. точку, равновесие которой в данной задаче следует рассмотреть;
второй этап — к выделенному объекту равновесия прикладывают заданные силы;
третий этап — выделенную точку или тело освобождают от связей, их действие заменяют реакциями;
четвертый этап — выбирают координатные оси и составляют уравнения равновесия;
пятый этап — решают уравнения равновесия;
шестой этап — проверяют правильность решения.
В задачах статики часто приходится определять реакции стержней. Необходимо установить, как действуют растягивающие и сжимающие силы в стержнях на точки крепления стержней или узлы. Когда стержень MN растянут
(рис. 5, а), его реакции на точки крепления направлены от этих точек М и N
внутрь стержня. Когда стержень сжат, его реакции направлены к точкам закрепления, т, е. наружу (рис, 5, б). Следовательно, можно сказать, что в растянутом стержне реакции направлены от узлов внутрь стержня, в сжатом к узлам наружу от стержня, по аналогии с деформированной пружиной.
Часто при решении задач трудно заранее определить направление реакций стержней. В этих случаях удобно считать стержни растянутыми и их реакции направлять от узлов.
Если решение задачи даст значение реакции со знаком минус, то в действительности имеет место не растяжение, а сжатие. Таким образом, реакции растянутых стержней будут положительными, а сжатых — отрицательными.
Пример 1. Груз подвешен на стержнях и находится в равновесии. Определить усилия в стержнях (рис. 6а).
1. Усилия, возникающие в стержнях крепления, по величине равны силам, с которыми стержни поддерживают груз (5-я аксиома статики) (рис.6а).
Определяем возможные направления реакций связей «жесткие стержни».
Усилия направлены вдоль стержней.
2. Освободим точку А от связей, заменив действие связей ихреакциями
3. Система находится в равновесии. Построим треугольник сил. Построение начнем с известной силы, вычертив вектор F в некотором масштабе.
Из концов вектора F проводим линии, параллельные реакциям
Пересекаясь, линии создадут треугольник (рис. 6в). Зная масштаб построений и измерив длину сторон треугольника, можно определить величину реакций в стержнях.
4. Для более точных расчетов можно воспользоваться геометрическими соотношениями, в частности теоремой синусов: отношение стороны треугольника к синусу противоположного угла — величина постоянная
Для данного случая:

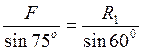




З а м е ч а н и е. Если направление вектора (реакции связи) на заданной схеме и в треугольнике сил не совпало, значит, реакция на схеме должна быть направлена в противоположную сторону.
Пример 2. Решение задач на равновесие плоской системы сходящихся сил
Дано: Груз подвешен на стержнях и канатах и находится в равновесии. Определить реакции стержней АВ и ВС. (рис. 7).
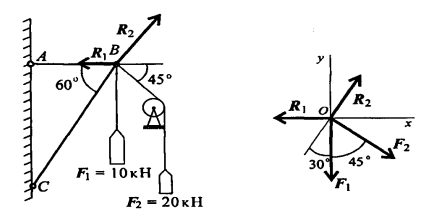
1. Определим вероятные направления реакций. Мысленно убираем стержень АВ, при этом стержень СВ опускается, следовательно точка В отодвигается от стены: назначение стержня АВ — тянуть точку В к стене.
Если убрать стержень СВ, точка В опустится, следовательно, стержень СВ поддерживает точку В снизу — реакция направлена вверх.
2. Освободим точку В от связей.
Пример 3. К кронштейну АВС в точке В подвешены два груза: груз g1 — 600 Н непосредственно и груз g 2 = 400 Н через отводной блокD (рис. 9, а). Определить реакции стержней АВ и ВС кронштейна.
В точке В пересекаются линии действия заданных сил G 1 и G 2 и искомых реакций стержней АВ и СВ, поэтому выделяем узел В (рис. 8, б), который в данной задаче рассматривается как объект равновесия. Прикладываем к этому узлу заданные силы G 1, направленную вертикально, и G 2, направленную вдоль троса. При этом учитываем, что неподвижный блок D изменяет направление силы, но не влияет на ее значение. Освобождаем узел В от связей, которые осуществляются стержнями АВ и ВС. Прикладываем вместо них реакции стержней ri и R 2, направляем их вдоль стержня от узла, т. е. полагаем, что оба стержня АВ и ВС растянуты. Выбираем координатные оси х и у (при выбранном направлении осей большинство проекций имеют знак плюс) и составляем уравнения равновесия:
1). Σ Fix = 0; R 1- G2 cos 45° + R2 cos 45° = 0;
Решив уравнения равновесия, находим:
R 1 = G2cos45° — R 2соз45° = 400 · 0,707 — (-1249) 0,707 = 1166 Н.
Знак минус перед численным значением реакции R2показывает, что стержень ВС не растянут, как предполагалось, а сжат.
Задание 1
1  | 2  |
3  | 4  |
5  | 6  |
7  | 8  |
9 F1  F2 F2 | 10 F1  F2 F2 |
Таблица1 –Данные по вариантам
| Вариант | № схемы | F1 | F2 | Вариант | № схемы | F1 | F2 |
| 1 | 1 | 6 | 7,4 | 16 | 6 | 7 | 9 |
| 2 | 2 | 4,2 | 10 | 17 | 7 | 11 | 6,2 |
| 3 | 3 | 8 | 6,2 | 18 | 8 | 14 | 8,4 |
| 4 | 4 | 12 | 12 | 19 | 9 | 8,5 | 10 |
| 5 | 5 | 3 | 12,6 | 20 | 10 | 7,2 | 7 |
| 6 | 6 | 4.5 | 10 | 21 | 1 | 10 | 6.5 |
| 7 | 7 | 4,6 | 7,2 | 22 | 2 | 6,8 | 4,6 |
| 8 | 8 | 8.2 | 11 | 23 | 3 | 12 | 5.2 |
| 9 | 9 | 5,4 | 6,8 | 24 | 4 | 13,6 | 8,4 |
| 10 | 10 | 4,8 | 7 | 25 | 5 | 14 | 6,8 |
| 11 | 1 | 9 | 11 | 26 | 6 | 12,6 | 9 |
| 12 | 2 | 11 | 14 | 27 | 7 | 14 | 12 |
| 13 | 3 | 5 | 8,5 | 28 | 8 | 7,5 | 5,8 |
| 14 | 4 | 12 | 7,2 | 29 | 9 | 9,8 | 10,5 |
| 15 | 5 | 14 | 10 | 30 | 10 | 14 | 12 |
Контрольные вопросы
1. Определить модуль равнодействующей системы сходящихся сил, если проекции слагаемых векторов равны: Flx = 50 Н; F2x = -30 Н; F3x = 60 Н; F4x = 70 Н;
2. В каком из указанных случаев плоская система сходящихся сил уравновешена?
3. Какая из приведенных ниже систем уравнений равновесия справедлива для изображенной на рис.9 системы сходящихся
4. По изображенным многоугольникам сил (рис. 10) решите, сколько сил входит в каждую систему, и какая из них уравновешена. (Обратить внимание на направление векторов.)

Практическое занятие № 02
Тема : Определение опорных реакций балок
Цель: Научиться составлять расчетные схемы балок и определять их опорные реакции.
Входной контроль
1. Пара сил и ее действие на тело.
2. Шарнирно-подвижная опора
3. Жесткая заделка (защемление)
Теоретический материал
Виды нагрузок
По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосредоточенной.
Часто нагрузка распределена по значительной площадке или линии (давление воды на плотину, давление снега на крышу и т.п.), тогда нагрузку считают распределенной.
В задачах статики для абсолютно твердых тел распределенную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 1).
q — интенсивность нагрузки; l — длина стержня;
G = ql равнодействующая распределенной нагрузки.
Дата добавления: 2020-04-08 ; просмотров: 3867 ; Мы поможем в написании вашей работы!
Источник