Определить расстояние между точками двумя способами

Расстояния между двумя точками

На данной странице калькулятор поможет рассчитать расстояние между двумя точками онлайн в плоскости и пространстве. Для расчета задайте координаты.

Расстояние между двумя точками — это длина отрезка, которая соединяет эти точки.

Расстояния между двумя точками

Формула вычисления расстояния между двумя точками A(x_a; y_a) и B(x_b; y_b) на плоскости:

Формула вычисления расстояния между двумя точками A(x_a; y_a; z_a) и B(x_b; y_b; z_b) в пространстве:

Вывод формулы для вычисления расстояния между двумя точками на плоскости

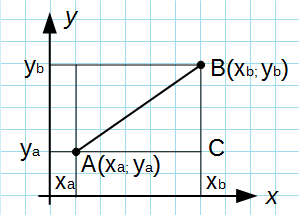
Из точек A и B опустим перпендикуляры на оси координат x и y.

Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:

Спомощью теоремы Пифагора, вычислим длину отрезка AB:

Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.

Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.

Источник

Определение расстояний по карте различными способами

↑ Масштабы карт и пользование ими

При создании топографических карт, спроецированные на уровенную поверхность линейные размеры всех объектов местности уменьшают в определенное количество раз. Степень такого уменьшения называется масштабом карты. Масштаб карты может быть выражен в численной форме (численный масштаб) или в графической (линейный, поперечный масштабы), в виде графика.

Расстояния по карте измеряют, пользуясь обычно численным или линейным масштабом. Более точные измерения выполняются с помощью поперечного масштаба.

На шкале линейного масштаба оцифрованы отрезки, соответствующие расстояниям на местности в метрах или километрах. Это облегчает процесс измерения расстояний, так как не требуется производить вычисления.

Определение по карте расстояний и площадей.Измерение расстояний.

При пользовании численным масштабом расстояние, измеренное на карте в сантиметрах, умножают на знаменатель численного масштаба в метрах.

Например, расстояние от пункта ГГС отм. 174,3 (кв. 3909 ) до развилки дорог (кв. 4314) на карте составляет 13,96 см, на местности оно будет: 13,96 х 500 = 6980 м. (карта масштаба 1: 50 000 У-34-85-А).

Если расстояние, измеренное на местности надо отложить на карте, то его надо разделить на знаменатель численного масштаба. Например, расстояние, измеренное на местности, равно 1550 м., на карте масштаба 1: 50 000 оно будет 3,1 см.

Измерения по линейному масштабу выполняют с помощью циркуля-измерителя. Раствором циркуля соединяют две контурные точки на карте, между которым надо определить расстояние, затем прикладывают к линейному масштабу и получают расстояние на местности. Криволинейные участки определяют по частям или при помощи курвиметра.

↑ Определение площадей.

Площадь участка местности определяют по карте чаще всего подсчетом квадратов координатной сетки, покрывающих этот участок. Величину долей квадратов определяют на глаз или с помощью специальной палетки. Каждый квадрат, образуемый линиями координатной сетки, соответствует : 1: 25 000 и 1: 50 000 – 1 км.кв., 1: 100 000 – 4 км.кв., 1: 200 000 – 16 км.кв.

Полезно помнить, следующие соотношение 2 х 2 мм., соответсвуют для масштабов:

1: 25 000 – 0,25 га = 0,0025 км.кв.

1: 50 000 – 1 га = 0, 01 км.кв.

1: 100 000 – 4 га = 0, 04 км.кв.

1: 200 000 – 16 га = 0, 16 км.кв.

Определение площадей отдельных участков проводится при отчуждении земельных участков для Министерства обороны.

Точность определения расстояний по карте. Поправка в длину маршрута.

Точность измерения линий, площадей по топографической карте. Приобрести седельные тягачи и грузовики по самым лучшим ценам, вы сможете на сайте auto-holland.ru. Все грузовые автомобили прошли предпродажную подготовку и инспекционный контроль (инструментальный, компьютерный и визуальный).

Точность измерения линий и площадей, в первую очередь, зависит от масштаба карты. Чем крупнее масштаб карты, тем точнее определяются по ней длины линий и площади. При этом точность зависит не только от точности измерений, но и от погрешности самой карты, неизбежно при ее составлении и печати. Ошибки могут достигать для равнинных районов 0, 5, а в горах до 0, 7 мм. Источником ошибок измерений также является деформация карты и сами измерения.

Абсолютно с такой же погрешностью определяются плоские прямоугольные координаты по топографическим картам вышеперечисленных масштабов.

↑ Поправка в расстояние за наклон линии.

Например, расстояние между двумя пунктами, измеренное по карте, на местности с углом наклона 12 градусов равно 9270 м. Действительное же расстояние между этими пунктами будет 9270 х 1.02 = 9455 м. Таким образом, при измерении расстояний по карте, необходимо вводить поправки за наклон линий (рельеф).

Прямолинейные расстояния большой протяженности в одной шестиградусной зоне могут быть рассчитаны по формуле:

Этот способ определения расстояния используется в основном при подготовке стрельбы артиллерии и при пуске ракет по наземным целям.

Источник

Расстояние между точками

На этой странице находится все необходимое, чтобы найти расстояние между двумя точками. Просто введите координаты точек и получите ответ и подробное решение с помощью наших онлайн-калькуляторов. Кроме того на сайте можно найти координаты середины отрезка.

Расстояние между двумя точками — это длина отрезка, соединяющего эти точки.

Расстояние между двумя точками на плоскости

Формула для нахождения расстояния между двумя точками A(x_a, y_a) и B(x_b, y_b) на плоскости:

^2 + <(y_b — y_a)^2>>> , где x_a и y_a — координаты первой точки A, x_b и y_b — координаты второй точки B.

Нахождение расстояния между двумя точками на плоскости сводится к решению треугольника, а точнее — нахождению его гипотенузы. Для этого используется теорема Пифагора. Посмотрите на рисунок.

Соединив отрезком точки A и B, а также опустив перпендикуляры на оси мы получим треугольник ABC. В этом треугольнике стороны AC и BC являются катетами прямоугольного треугольника, а AB — его гипотенузой. Длины катетов AC и BC найти довольно просто:

Осталось применить теорему Пифагора и получить сторону AB, которая является гипотенузой прямоугольного треугольника и расстоянием между точками A и B:

Подставив вместо отрезков AC и BC их длины, получим итоговую формулу расстояния между двумя точками:

Источник

Определение расстояний между двумя точками

Определение расстояний между двумя точками фактически сводится к нахождению истинной длины (натуральной величины) отрезка прямой линии. Эту задачу можно решить тремя способами, два из которых нами уже рассмотрено:

1. способом замены плоскостей проекций (прямую общего положения преобразовать в прямую уровня, (см. рис. 2.1-а);

2. способом вращения (прямую общего положения преобразовать в прямую уровня, (см. рис.2.3);

3. способом прямоугольного прямоугольника.

Определение натуральной величины отрезка прямой общего положения и углов его наклона к плоскостям проекций способом прямоугольного треугольника

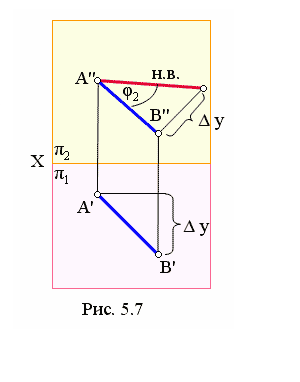
Способ прямоугольного треугольника можно сопоставить со способом замены плоскостей. Если новую осьХ₁ совместить с проекцией АВ (на рис. 5.6 ось Х₁ надо совместить с проекцией А»В»), тогда вместо А’А_х = А_х1 А IV и В’В_х = В_х1 В IV надо от А» отложить разность Δ y (рис. 5.7). Угол φ₂ является углом наклона прямой АВ к фронтальной плоскости проекций.

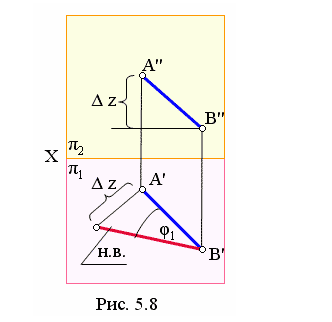
На рис. 5.8 определена натуральная величина отрезка АВ относительно горизонтальной плоскости проекций. Угол φ₁ является углом наклона прямой АВ к горизонтальной плоскости.

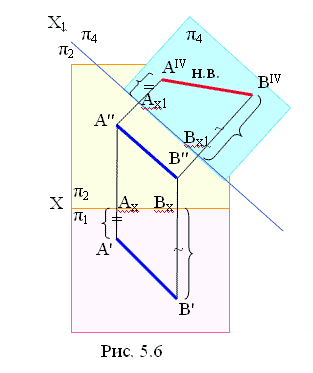
Теперь вы должны выполнить задачу 2 контрольной работы

Источник

Как найти расстояние между двумя точками?

Расстоянием между точками также называют прямую,
у которой одна из точек это начало, а соответственно
другая конец. Найти расстояние между этими
двумя точками, значит найти длину прямой,
связывающей точки.

Есть много разных способов найти расстояние между
двумя точками, но самый универсальный, на мой взгляд,
это найти расстояние взяв за основу Теорему Пифагора.
Исходя из этой теоремы, можно сказать, что в нашем
случае расстоянием(прямой), является гипотенуза,
а чем тогда являются точки, сейчас разберемся.

Формулировка великой Теоремы Пифагора звучит так:
в прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов. Или же кратко, формулой:
\( c^2 = a^2 + b^2 \) где c — это гипотенуза, a и b — катеты.

Формулировка этой теоремы применяется почти всегда и везде,
где нужно найти расстояние от чего-то до чего-то. Сейчас, мы
используя эту теорему найдем расстояние между точками.

Итак, для примера возьмем точки с координатами
первой точки — x1 = 0; y1 = 4, второй точки — x2 =3; y2 = 0.
Как же нам теперь выразить точки через катеты a и b ?
Читайте дальше, все гениальное просто.

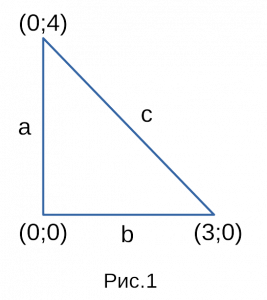
На рисунке 1 мы изобразили для наглядности
прямоугольный треугольник, с координатами
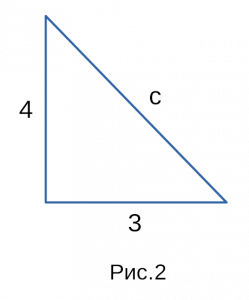
которые мы взяли для примера. На рисунке 2
тот же самый прямоугольный треугольник,
только без координат! Эти два прямоугольных
треугольника идентичные, поэтому вернемся
к Теореме Пифагора.

Заменяем длины катетов a и b, из Теоремы Пифагора,
на разность координат точек. ​Взгляните на формулу,
которая получилась:

Подставляем наши координаты:

В итоге получилось, что расстояние в нашем примере
равно 5(корень из 25). Как видите все просто, и вы можете
смело применять эту формулу, решая не только задачи,
но и на практике, находя расстояние зная только две точки.

Источник