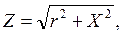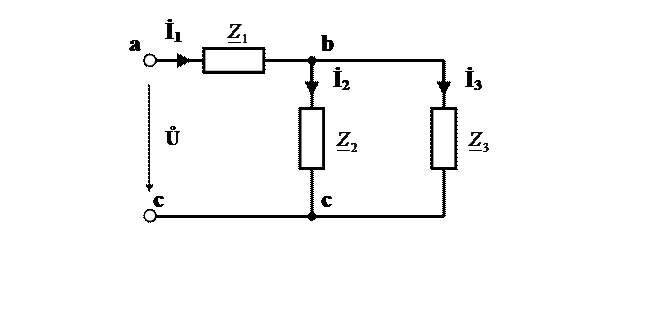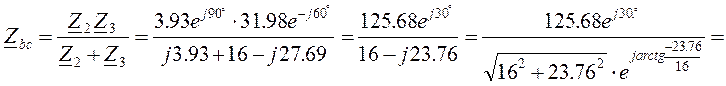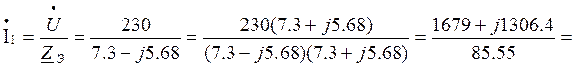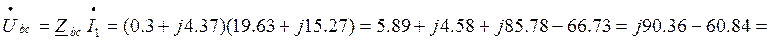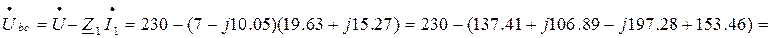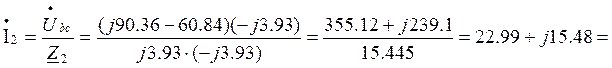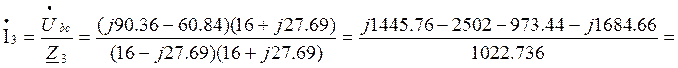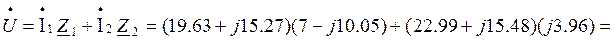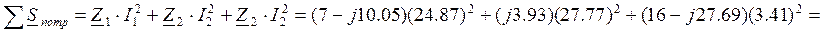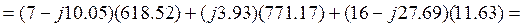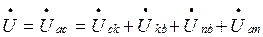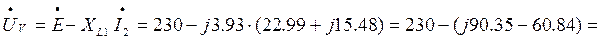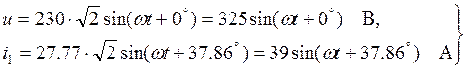Как измерить мощность с помощью двух ваттметров
При измерении мощности в трехфазных цепях двумя ваттметрами есть возможность не только сэкономить один ваттметр, но и по их показаниям судить ориентировочно о значении коэффициента мощности трехфазного электроприемника.
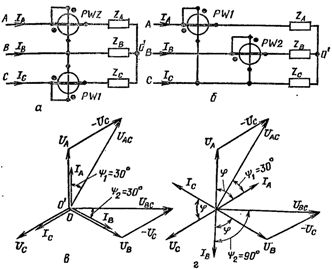
Например, если нагрузка в фазах активная и симметричная то показания обоих ваттметров будут одинаковы. Это видно из векторной диаграммы (рис. 1, в).
Токи совпадают по направлению с фазными напряжениями (приемник соединен звездой): ток I А с напряжением UА, а ток I В с напряжением UB, так как нагрузка активная. Угол ψ1 между UAC и I А равен 30 о , и угол ψ 2 между U BC и IB также равен 30 о .
Рис. 1 . Схема включения двух ваттметров в трехпроводную сеть (а, б) и векторные диаграммы напряжений и токов при cos ф=1 (в) и cos ф=0,5 (г).
Значения мощности, измеряемые ваттметрами, определяются одинаковыми выражениями:
Рw1 = UAC I Аcos ψ1 = UлIл cos30°,
Pw1 = U BC IB cosψ2 = UлIл cos30°
Если нагрузка носит активно-индуктивный характер и косинус фи равен 0,5, то есть угол φ = 60°, то угол ψ1 = 30°, а угол ψ 2 = 90° (рис. 1, г).
Показания ваттметров будут следующими:
Рw1 = UлIл cos30°
Pw1 = UлIл cos90°
Если показания одного из ваттметров становятся равными нулю, это значит, что косинус фи уменьшился до 0,5.
Из диаграммы также видно, что если косинус фи в сети станет меньше 0,5, то есть угол φ будет больше 60° , то угол ψ 2 станет больше 90°, а это приведет к тому, что показания второго ваттметра станут отрицательными, стрелка прибора начнет отклоняться в другую сторону (обычно в современных ваттметрах предусмотрен переключатель направления тока в подвижной катушке). Общая мощность в этом случае равна разности показаний ваттметров.
Если нагрузка симметрична, то по показаниям двух ваттметров можно точно вычислить значение cos φ по формуле
cos φ = P/S = P/(√ P 2 + Q 2 ) ,
где P = Рw1 + Рw2 — активная мощность трехфазного электроприемника, Вт, Q = √ 3 ( Рw1 + Рw2 ) — реактивная мощность трехфазного электроприемника. Последнее выражение показывает, что если разность показаний двух ваттметров умножить на √ 3 , получится значение реактивной мощности трехфазного электроприемника.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
Расчет сложных цепей переменного тока. Линейные электрические цепи синусоидального тока/
Страницы работы
Содержание работы
Кафедра электротехники и электрических машин
Тема: «Расчет сложных цепей переменного тока»
Выполнил: студент I курса 7145 гр. ИЭАСХ
заведующий кафедрой, доцент
Задача 1.2 Линейные электрические цепи синусоидального тока
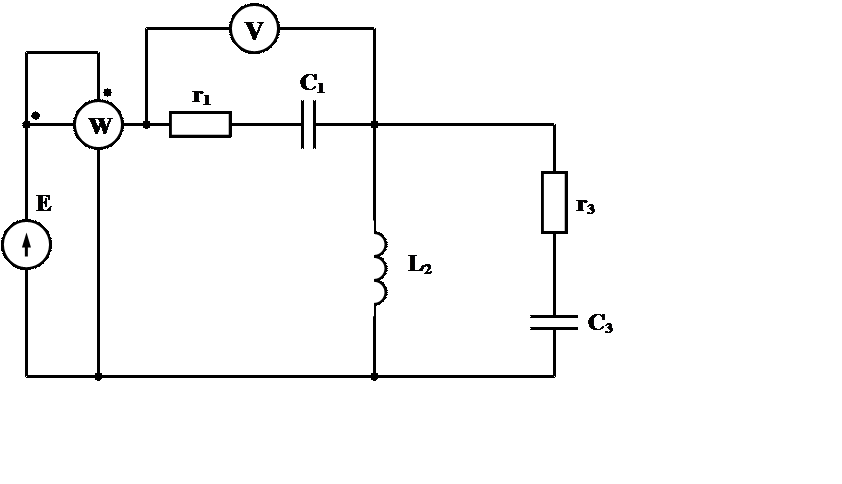
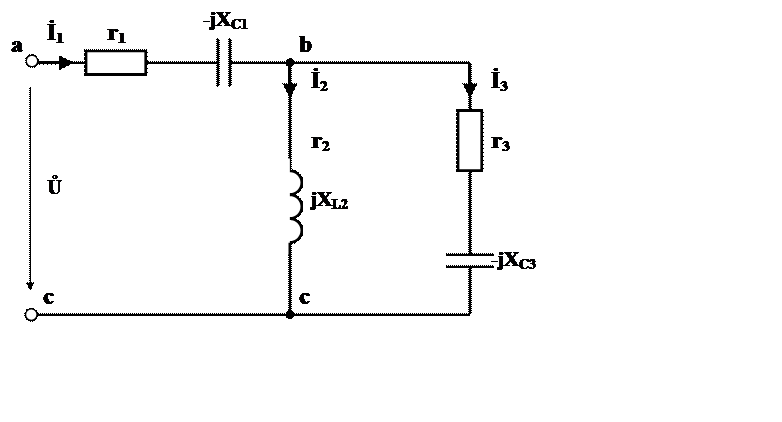
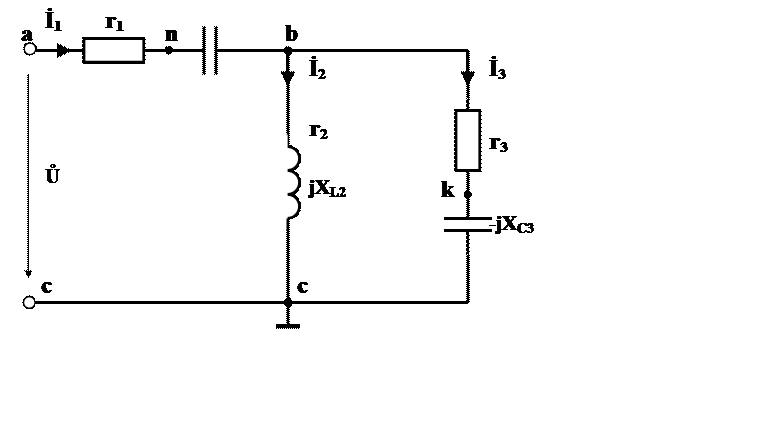
Дана электрическая схема (рис. 1), выполнить следующее:
1) определить токи во всех ветвях цепи и напряжения на отдельных участках цепи. Найти комплексы действующих значений токов во всех ветвях и их мгновенные значения;
2) составить баланс мощностей (активной, реактивной, полной);
3) построить в масштабе на комплексной плоскости топографическую диаграмму напряжений для замкнутых контуров, совмещенную с векторной диаграммой токов;
4) определить показания вольтметра и ваттметра;
5) построить графики мгновенных значений тока и напряжения, подведенных к ваттметру.
Е = 230 В; C1 = 317 мкФ; L2 = 12,5 мГн; r1 = 7 Ом;
f = 50 Гц; C3 = 115 мкФ; r3 = 16 Ом;
1. Определение токов во всех ветвях цепи и напряжения на отдельных участках цепи
Наиболее распространенным методом расчета таких цепей является метод эквивалентных преобразований. Этот метод заключается в последовательной, начиная с конца схемы, замене сопротивлений всех элементов электрической цепи одним эквивалентным с последующим использованием закона Ома.
Определим сопротивления реактивных элементов цепи:
; 
, где ω = 2πf = 2∙3,14∙50 = 314 с -1 – угловая частота.
Ом;
Ом;
Ом.
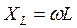
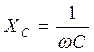
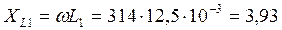
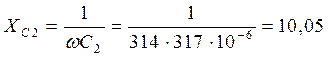
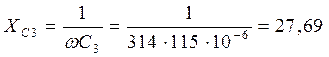
Расчет выполняем в комплексной форме с последующим переходом к аналитическим выражениям токов в следующей последовательности:
1. Задаемся положительным направлением токов в ветвях цепи;
2. Записываем электрические сопротивления ветвей цепи в комплексной форме:
Ом;
Ом;
Ом.
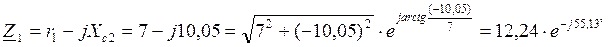
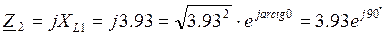
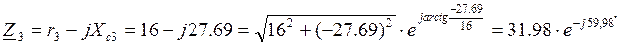
Модуль и аргумент комплексного сопротивления ветвей цепи определяются по формулам
, 
.
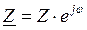
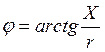
3. Электрическая схема рис. 2 заменяется эквивалентной с изображением ветвей полными электрическими сопротивлениями в комплексной форме (рис. 3).
4. Заменяем два параллельно соединенных сопротивления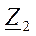 
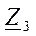
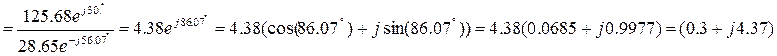
и 
одним эквивалентным
Ом.
5. Эквивалентное сопротивление всей цепи
Ом.
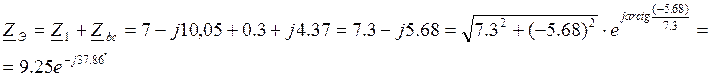
6. Находим ток на входе цепи
А.
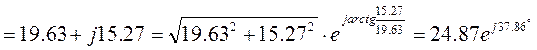
7. Для определения токов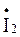 
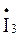
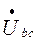
и 
найдем напряжение 
. Это напряжение можно найти двумя способами:
а) по закону Ома
В;
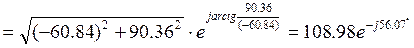
б) по второму закону Кирхгофа
В;
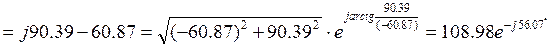
8. Токи в параллельных ветвях
А;
А.
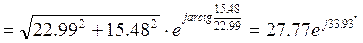
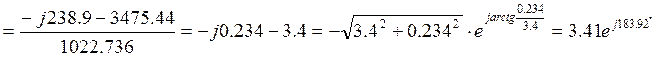
9. Проверяем правильность расчета по первому и второму закону Кирхгофа:
по первому закону Кирхгофа имеем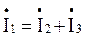 
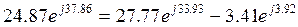
, то есть
А – верно с учетом погрешности.
по второму закону Кирхгофа, для «abcda»
В.
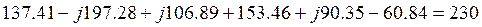
2. Составление баланса мощностей
Баланс мощностей заключается в равенстве суммарных, отдаваемых источником электрической энергии и потребляемых электрофизическими элементами электрической цепи
, где 
— сумма комплексных мощностей источников электрической энергии;
— сумма комплексных мощностей электрофизических элементов электрической цепи.
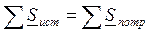
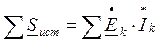
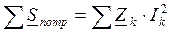
Для нашей электрической цепи
В;
ВА.
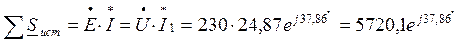
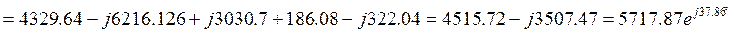
Активная мощность Р = 4515,72 Вт;
Реактивная мощность Q = 3507,47 вар.
3. Построение в масштабе на комплексной плоскости топографической диаграммы напряжений для замкнутых контуров, совмещенной с векторной диаграммой токов
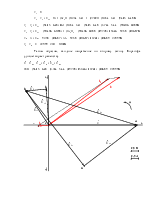
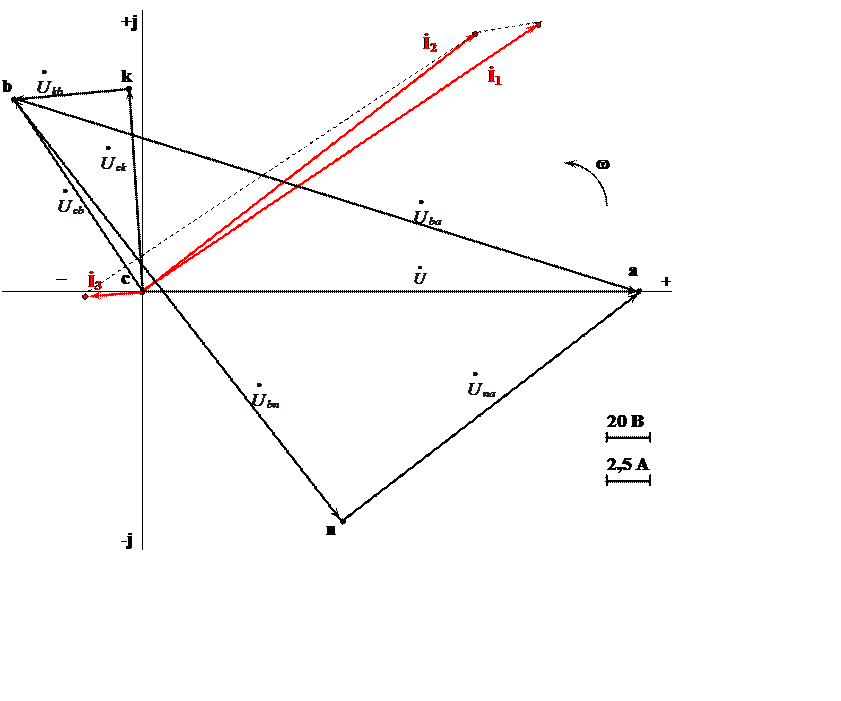
Откладываем в масштабе векторы токов I1, I2, I3 на комплексной плоскости. Для суждения о напряжениях между различными точками электрической цепи строим топографическую диаграмму в масштабе напряжения. Топографическая диаграмма строится из замкнутого контура, идя против направления тока в элементах цепи. Все векторы падений напряжений на элементах цепи замкнутого контура имеют определенное направление (рис. 4):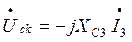 
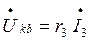
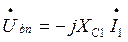
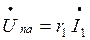
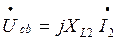
— отстает от тока İ3 на 90°; 
— совпадает по фазе с током İ3; 
— отстает от тока İ1 на 90°; 
— совпадает по фазе с током İ1. 
— опережает ток İ2 на 90°.
Совмещенная векторная диаграмма токов и топографическая диаграмма напряжений представлена на рисунке 5.
В
В
В
В
В
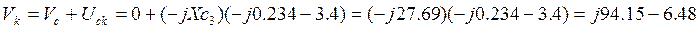
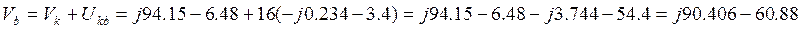
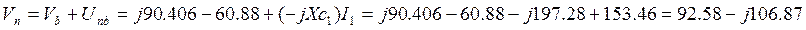
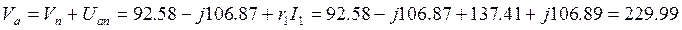
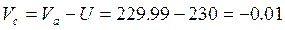
Таким образом, входное напряжение по второму закону Кирхгофа удовлетворяет равенству
В
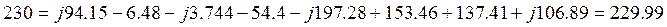
4. Определение показания вольтметра и ваттметра
При аналитическом определении показаний приборов (вольтметров, амперметров, ваттметров) необходимо соответствующие расчеты выполнять в комплексах Действующих значений токов и напряжений. Показания приборов определяются модулем комплекса соответствующей электрической величины.
Показание вольтметра определяем из уравнения, составленного по второму закону Кирхгофа для контура «abca» (рис. 1).
, откуда
В.
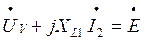
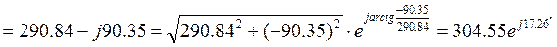
Показание вольтметра Uv = 304,55 В.
Ваттметр показывает активную мощность
, где U и I – действующие значения напряжения и тока;
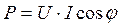
φ – угол сдвига по фазе между напряжением и током.
При определении показания ваттметра необходимо учитывать ориентацию тока и напряжения относительно к генераторным зажимам (зажимам, обозначенным звездочками).
В нашем случае одинаково ориентированы относительно зажимов, обозначенных звездочками.
Ток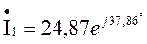 
А.
Напряжение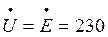 
В.
Сдвиг по фазе между векторами напряжения и тока
.
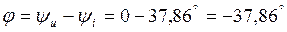
Показания ваттметра равно
Вт.
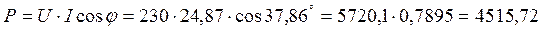
Можно определить показание ваттметра через комплексную мощность
, где 
– комплекс напряжения, приложенного к ваттметру, В;
– сопряженный комплекс тока, протекающего через токовую обмотку ваттметра, А.
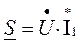
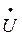
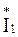
Используем алгебраическую форму записи комплекса напряжения и тока
В,
А,
ВА
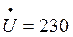
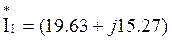
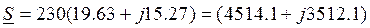
Показание ваттметра равно действительной части комплексной мощности
Вт.
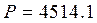
5. Построение графиков мгновенных значений тока и напряжения, подведенных к ваттметру
Для построения временных характеристик тока и напряжения, подведенных к ваттметру, запишем их мгновенные значения
Для расчета координат точек кривых i1 = f1(ωt) и u = f2(ωt) составляем таблицу 1.
Источник
