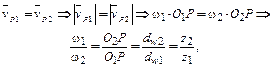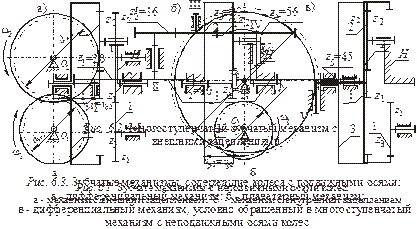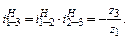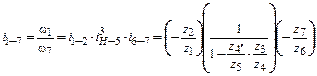Определить передаточное отношение u13 графическим способом профессора семенова приближенный метод

Сложными зубчатыми механизмами называются механизмы с зубчатыми передачами с числом зубчатых колес больше двух. Это могут быть механизмы с оригинальными структурными схемами или механизмы, образованные последовательным и (или) параллельным соединением простейших типовых зубчатых механизмов.
Механизмы, в которых кинематические цепи образуют один или несколько замкнутых контуров и в которых входной поток механической мощности в процессе передачи и преобразования делится на несколько потоков, а затем суммируется на выходном звене, называются многопоточными механизмами. Распределение передаваемых усилий по нескольким кинематическим парам уменьшает нагрузку на элементы пар и позволяет существенно уменьшать габаритные размеры и массу механизмов. Многозонный контакт звеньев механизма существенно увеличивает жесткость механизма, а за счет осреднения ошибок и зазоров, уменьшает мертвый ход и кинематическую погрешность механизма. Однако, за счет образования в структуре механизма внутренних контуров, число избыточных или пассивных связей в механизме увеличивается. Поэтому при изготовлении и сборке механизма необходимо либо повышать точность деталей, либо увеличивать зазоры в кинематических парах.
Сложные зубчатые механизмы, в которых ось хотя бы одного колеса подвижна, называются планетарными механизмами. К типовым планетарным механизмам относятся:

однорядный планетарный механизм;
двухрядный планетарный механизм с одним внешним и одним внутренним зацеплением
двухрядный планетарный механизм с двумя внешними зацеплениями;
двухрядный планетарный механизм с двумя внутренними зацеплениями.

Элементы планетарного механизма имеют специальные названия:

зубчатое колесо с внешними зубьями, расположенное в центре механизма называется «солнечным»;
колесо с внутренними зубьями называют «короной» или «эпициклом»;
колеса, оси которых подвижны, называют «сателлитами»;
подвижное звено, на котором установлены сателлиты, называют «водилом» . Звено водила принято обозначать не цифрой, а латинской буквой h.

В таблице 15.1 приведены структурные схемы типовых планетарных механизмов, а также диапазоны рекомендуемых передаточных отношений и ориентировочные значения КПД при этих передаточных отношениях.

Источник

КИНЕМАТИЧЕСКИЙ АНАЛИЗ ЗУБЧАТЫХ МЕХАНИЗМОВ

Целью работы является приобретение умения определять передаточное отношение зубчатых механизмов и абсолютные угловые скорости их звеньев.

6.1. Основные сведения из теории

Зубчатые механизмы в большинстве своем служат для передачи вращательного движения от одного вала к другому, при этом может изменяться величина и направление угловой скорости. Различают зубчатые механизмы с неподвижными осями колес (рис. 6.1 и 6.2) и механизмы, имеющие в своем составе зубчатые колеса (сателлиты), оси которых движутся в пространстве (рис. 6.3,а и 6.3,б).

В механизме зубчатые колеса, например j и k, вращаются в общем случае с разными угловыми скоростями ω_j и ω_k соответственно. Отношение этих угловых скоростей называется передаточным отношением и обозначается буквой i с соответствующими индексами. Таким образом, величины

(6.1)

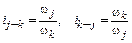
являются передаточными отношениями одной и той же передачи, только в первом случае входным звеном считается колесо j, а выходным – колесо k, а во втором случае наоборот. Из выражения (6.1) следует, что

(6.2)

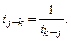
В простейших зубчатых механизмах, состоящих из двух зубчатых колес 1 и 2, оси которых неподвижны (рис. 6.1), передаточное отношение можно выразить не только через отношение угловых скоростей, но и через отношение их чисел зубьев. Действительно, в полюсе Р имеют место следующие соотношения:

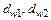
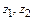
где – начальные диаметры колес 1 и 2; – числа зубьев колес 1 и 2.

Таким образом, для простейшего зубчатого механизма с цилиндрическими зубчатыми колесами, оси которых неподвижны, можно записать

(6.3)

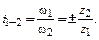
Знак «+» в формуле (6.3) принято ставить в том случае, когда угловые скорости колес 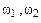одного направления (внутреннее зацепление, рис. 6.1,б).

В тех случаях, когда необходимо передать движение между валами, расположенными далеко друг от друга, и обеспечить большое передаточное отношение, используют сложные (многоступенчатые) зубчатые механизмы. На рис. 6.2 дан пример многоступенчатого механизма, содержащего зубчатые колеса с неподвижными осями. Общее передаточное отношение такого механизма равно произведению передаточных отношений всех зацепляющихся пар колес

(6.4)

(6.5)

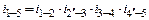
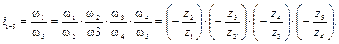
Зубчатые механизмы, изображенные на рис 6.3, содержат колесо 2 (сателлит), ось которого перемещается в пространстве с помощью звена Н, называемого водилом, а также колеса 1 и 3 (рис. 6.3,а), вращающиеся вокруг неподвижной центральной оси и называемые центральными. В механизме на рис. 6.3,б одно из центральных колес (колесо 3) – неподвижно.

Если степень подвижности W такого механизма равна единице (рис. 6.3,б), то он называется планетарным, если двум и более – дифференциальным.

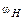
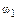
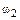
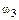
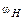
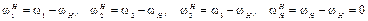
Передаточное отношение механизма можно определить с помощью метода обращения движения. Суть его заключается в том, что всем звеньям механизма мысленно дается дополнительное вращение с угловой скоростью , равной по величине угловой скорости водила в направлении, противоположном вращению водила. Если обозначить абсолютные угловые скорости (то есть скорости относительно неподвижной системы координат) звеньев реального механизма с сателлитами на рис. 6.3,а через , , , (нижние индексы соответствуют номеру звеньев), то в обращенном движении те же звенья будут иметь новые угловые скорости (обозначим их с верхним индексом Н):

Тогда водило и оси сателлитов становятся как бы неподвижными и получается так называемый обращенный механизм, представляющий собой многоступенчатый механизм с неподвижными осями колес (рис. 6.3,в).

Передаточное отношение от первого звена к третьему для обращенного механизма запишется в следующем виде

(6.6)

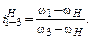
Формула (6.6) называется формулой Виллиса. Здесь 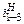– передаточное отношение простой передачи при остановленном водиле, равное

Задаваясь двумя скоростями по формуле (6.6) можно определить третью скорость. Заметим, что формулу Виллиса можно записать для двух любых звеньев. Например, по формуле

(6.7)

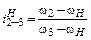
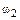
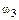
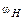
можно определить угловую скорость сателлита при известных скоростях и .

Если в дифференциальной передаче (рис. 6.3,а) одно из колес, относящихся к основным звеньям, закрепить, то получится планетарный механизм, обладающий одной степенью подвижности. В передаче на рис. 6.3,б остановлено центральное колесо 3. Движение передается с водила на центральное колесо 1 или наоборот. Формулу для передаточного отношения можно получить из формулы (6.6), если положить в ней .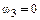

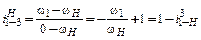
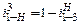
. (6.8)

Индекс 3 вверху означает, что 3 колесо неподвижно.

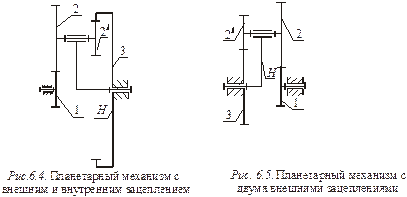
Для планетарного механизма, изображенного на рис 6.4,

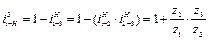
На рис. 6.5. показан планетарный механизм, составленный из двух пар внешнего зацепления. Для него передаточное отношение равно

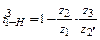
или при передаче вращения от водила к колесу 1

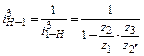
В некоторых случаях целесообразно использовать комбинированные зубчатые механизмы, составленные из передач разных типов. Например, механизм, показанный на рис. 6.6, имеет быстроходную цилиндрическую ступень, промежуточную планетарную ступень и тихоходную ступень, составленную из цилиндрических колес. Передаточное отношение всего механизма равно

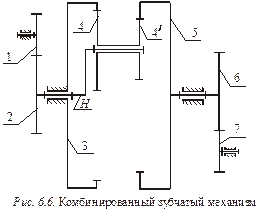При проектировании планетарных механизмов, подборе чисел их зубьев требуется не только обеспечить заданное передаточное отношение, но и выполнить следующие дополнительные условия.

1. Условие соосности выражает обязательное требование: оси центральных колес механизма должны лежать на одной прямой. При несоблюдении этого условия сателлит не сможет перекатываться одновременно по обоим центральным колесам механизма.

В механизмах с цилиндрическими колесами условие соосности выражает равенство межосевых расстояний в каждом из зацеплений центрального колеса и сателлита. Если колеса нарезаны без смещения и модули всех колес равны, то условие соосности может быть записано через числа зубьев колес. Например, для механизма с двухвенцовым сателлитом внешнего зацепления (рис. 6.5):

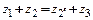
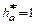
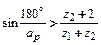
2.Условие соседствасателлитов. В планетарных механизмах, как правило, устанавливается не один, а несколько (чаще всего два или три) сателлитов. При этом вершины зубьев соседних сателлитов не должны касаться друг друга. Если колеса нарезаны без смещения стандартным инструментом ( ), то условие соседства сателлитов может быть выражено формулой

, (6.9)

где 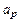– число сателлитов.

Для механизмов, имеющих двухвенцовые сателлиты, в числитель формулы (9) вместо 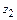следует подставлять число зубьев большего из венцов сателлита.

3. Условие сборки выражает соотношение между числами зубьев колес планетарного механизма, при котором возможно равномерное распределение нескольких сателлитов по окружности:

, (6.10)

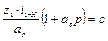
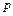
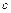
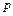
где и – любые целые числа, причем может быть равно нулю.

Это условие требуется проверять для механизмов с несколькими сателлитами.

6.2. Порядок выполнения работы

1. Ознакомиться с механизмом, прокрутить его за ведущий вал. Составить структурную схему. Пронумеровать все звенья.

2. Определить степень подвижности механизма.

3. Подсчитать числа зубьев колес. Разбить механизм по ступеням. Определить передаточное отношение каждой ступени.

4. Определить передаточное отношение всего механизма.

5. Проверить вычисленное значение передаточного отношения. Для этого поворачивают ведущий вал на такое целое число оборотов, чтобы ведомый вал повернулся тоже на целое число оборотов. Отношение числа оборотов ведущего вала к числу оборотов вала ведомого должно быть равно передаточному отношению механизма. Например, при i = 4,3 ведущий вал надо повернуть на 43 оборота, а ведомый вал за это время повернется на 10 оборотов.

6. Определить угловые скорости всех звеньев механизма, принимая скорость ведущего звена 10 с –1 .

7. Для планетарного механизма выразить через числа зубьев условие соосности и проверить на модели механизма его справедливость.

8. Для планетарного механизма определить из условия соседства сателлитов их максимально возможное число по формуле

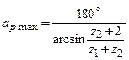
Проверить справедливость полученного результата вычерчиванием.

9. Проверить возможность сборки планетарного механизма при этом числе сателлитов.

10. Оформить отчет.

6.3. Вопросы для самоконтроля

1. Какие механизмы называются планетарными и дифференциальными?

2. Какой вид имеет формула Виллиса, устанавливающая зависимость между угловыми скоростями трех звеньев, входящих в состав элементарного дифференциального механизма?

3. Что называется передаточным отношением зубчатой передачи?

4. Как определить передаточное отношение простейшей зубчатой передачи с неподвижными осями колес?

5. Как определить передаточное отношение многоступенчатого зубчатого механизма?

6. Как определить передаточное отношение планетарного механизма?

7. Как выразить угловую скорость сателлита через угловую скорость ведущего звена?

8. Как отличить планетарный механизм от механизма, составленного из колес с неподвижными осями?

9. В чем заключается условие соосности в планетарном механизме?

10. В чем заключается условие соседства сателлитов?

11. В чем заключается условие сборки в планетарном механизме?

Источник