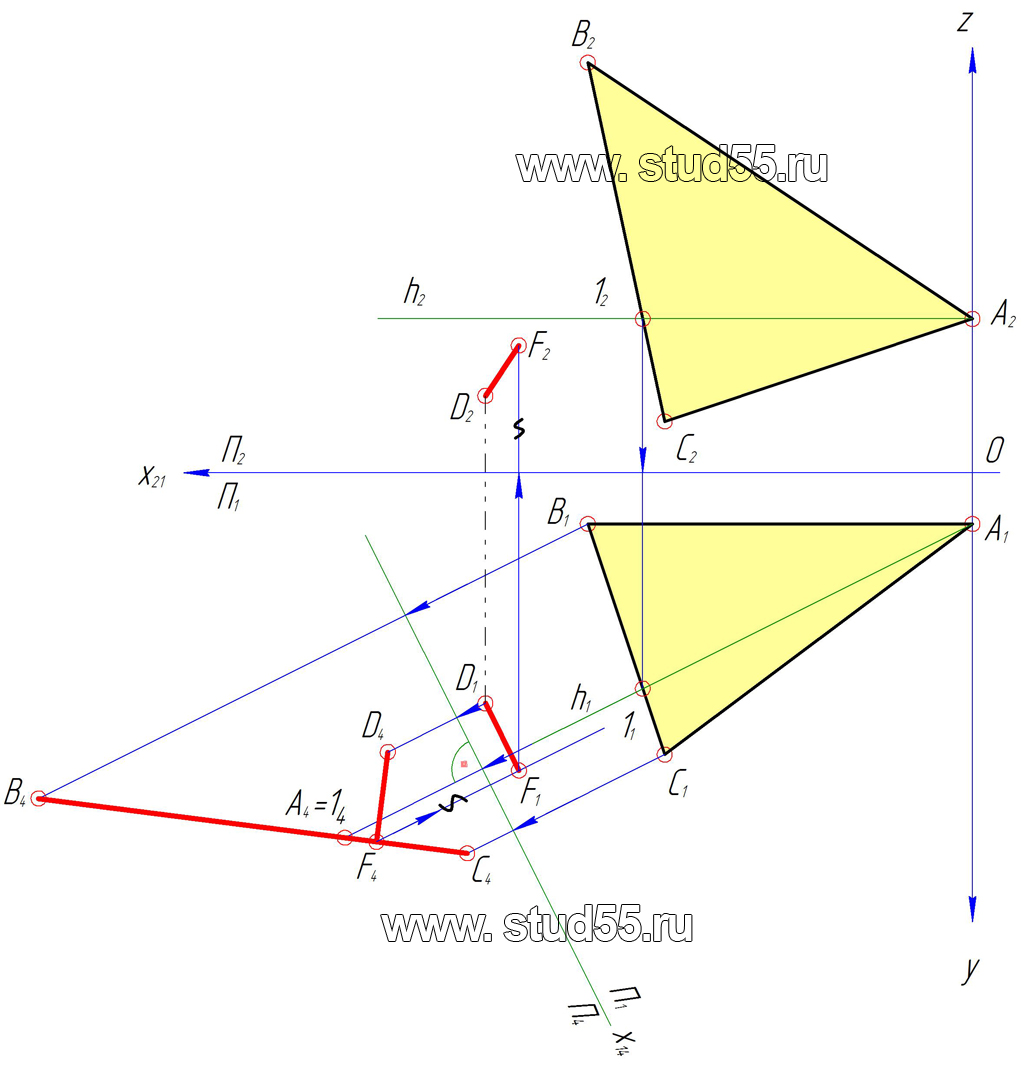
- Построить натуральную величину треугольника авс
- Способ замены плоскостей проекций
- Метод плоскопараллельного перемещения
- Метод прямоугольного треугольника
- Определить натуральную величину треугольника
- Замена плоскостей проекций
- Плоскопараллельное перемещение
- Способ вращения вокруг фронтали
- 58. Способ замены плоскостей проекций
- Начертательная геометрия, решение задач №6 и 8 ОмГУПС
- >>>Назад к решению задачи №5
- З а д а ч а 6
- З а д а ч а 8
Построить натуральную величину треугольника авс
Определить натуральную величину треугольника авс — можно тремя основными способами: (1) заменой плоскостей проекций, (2) методом прямоугольного треугольника и (3) вращением вокруг проецирующей оси или плоскопараллельным перемещением. Цель преобразования чертежа — построить проекцию треугольника АВС соответствующую натуральной величине.
В примерах, в качестве опорной прямой использована фронталь треугольника. Все алгоритмы могут использовать любую прямую частного положения. Для понимания использования фронтали, поверните чертёж на 180°.
Способ замены плоскостей проекций
Найти натуральную величину треугольника заменой плоскостей можно за два этапа: (1) перевести известную линию треугольника в проецирующее положение и (2) построить проекцию, плоскость которой параллельна плоскости треугольника, при которой плоская фигура проецируется в натуральную величину. Для первой замены, в плоскости общего положения следует выбрать фронталь или горизонталь.
В плоскости треугольника АВС проведена фронталь f. Перпендикулярно фронтали построена плоскость проекций П5, которая заменяет П1. На П5 треугольник АВС проецируется в отрезок. Вторая замена проекции выполнена параллельно АВС A6B6C6=АВС .
Метод плоскопараллельного перемещения
Определить натуральную величину треугольника способом плоскопараллельного перемещения можно за два этапа: первое перемещение переводит треугольник АВС в проецирующее положение, второе — совмещает с плоскостью параллельной плоскости проекций.
Произвольным плоскопараллельным перемещением выполнено преобразование положения треугольника АВС до горизонтально проецирующего положения f⊥П1. Аналогично методу замены плоскостей, первое перемещение преобразует горизонтальную проекцию треугольника в отрезок прямой. Второе перемещение выполнено до положения АВС параллельно фронтальной плоскости.
Метод прямоугольного треугольника
При вращении треугольника вокруг f, вершины перемещаются по окружностям во фронтально проецирующих плоскостях. Фронтальные проекции траектории вращения вершин АВС представлены перпендикулярами к f. Радиус вращения одной из вершин построен способом прямоугольного треугольника. B 0
2 — положение вершины треугольника в плоскости параллельной фронтальной проекции и проходящей через ось вращения f.
Источник
Определить натуральную величину треугольника
— можно по ортогональной проекции, относительно которой, плоскость треугольника параллельна.
Замена плоскостей проекций
Построение натуральной величины треугольника методом замены плоскостей — в общем случае, исходные плоскости П1/П2 переведены в П5/П4, так что плоскость исходного треугольника параллельна П5, а собственно треугольник проецируется в равный себе, так как каждый отрезок (сторона) треугольника параллельна плоскости проекций.
- На горизонтальной проекции, в треугольнике ABC проведена фронталь f=AF (A1F1║OX).
- Фронтальная проекция f2 определена по проекционной связи F1F2 с условием F2∈B2C2.
- Замена П1 на П4⊥f — в результате ABC занимает положение проецирующее на П4. A4B4C4 — проецируется в один отрезок, и угол φ соответствует углу наклона плоскости треугольника ABC к фронтальной плоскости проекций П2.
- П5║ABC заменяет П2. A5B5C5=ABC — натуральная величина заданного треугольника.
Начальный выбор фронтали произволен, и возможно выбрать для решения задачи любую линию частного положения лежащую в плоскости треугольника: фронталь, горизонталь или профильную прямую.
Плоскопараллельное перемещение
Используюя способ плоскопараллельного перемещения, выполняется преобразование исходных проекций до положения треугольника параллельно одной из исходных плоскостей проекций.
- Плоско-параллельное перемещение до положения f⊥П1
∠γ — наклон плоскости треугольника к фронтальной плоскости проекции. - Приведение вращением вокруг фронтально проецирующей оси до ABC║П2
R на первом этапе показывает эквивалентность плоскопараллельного перемещения и метода вращения.
Способ вращения вокруг фронтали
- В плоскости треугольника выбрана горизонталь f=AF
- Методом прямоугольного треугольника определён радиус R вращения точки C вокруг f.
- |R|=|fC|=|f2C 0
2 | — максимальное удаление точки C от оси вращения, при котором плоскость треугольника занимает положение параллельное фронтальной плоскости проекций. - B 0
2 определена как пересечение F2C 0
2 с перпендикуляром к фронтальной проекции оси вращения f2
Аналогично, можно решить задачу определения натуральной величины треугольника вращением вокруг горизонтали или совмещением плоскости фигуры с горизонтальной плоскостью проекции вращением вкруг горизонтального следа плоскости.
Источник
58. Способ замены плоскостей проекций
Сущность этого способа заключается в том, что заменяют одну из плоскостей на новую плоскость, расположенную под любым углом к ней, но перпендикулярную к незаменяемой плоскости проекции. Новая плоскость должна быть выбрана так, чтобы по отношению к ней геометрическая фигура занимала положение, обеспечивающее получение проекций, в наибольшей степени удовлетворяющих требованиям условий решаемой задачи. Для решения одних задач достаточно заменить одну плоскость, но если это решение не обеспечивает требуемого расположения геометрической фигуры, можно провести замену двух плоскостей.
Применение этого способа характеризуется тем, что пространственное положение заданных элементов остается неизменным, а изменяется система плоскостей проекций, на которых строятся новые изображения геометрических образов. Дополнительные плоскости проекций вводятся таким образом, чтобы на них интересующие нас элементы изображались в удобном для конкретной задачи положений.
Рассмотрим решение четырех исходных задач способом замены плоскостей проекций.
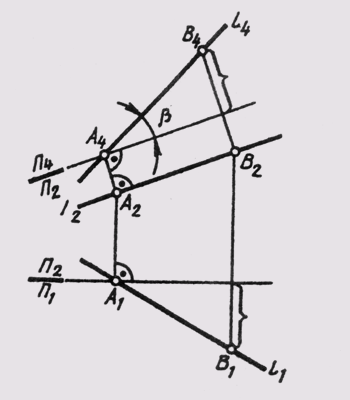
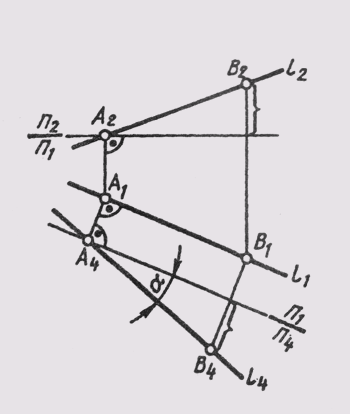
1. Преобразовать чертеж прямой общего положения так, чтобы относительно новой плоскости проекций прямая общего положения заняла положение прямой уровня.
Новую проекцию прямой, отвечающей поставленной задаче, можно построить на новой плоскости проекций П4, расположив ее параллельно самой прямой и перпендикулярно одной из основных плоскостей проекций, т. е. от системы плоскостей П1_|_П2 перейти к системе П4 _|_ П1 или П4 _|_ П2. На чертеже новая ось проекций должна быть параллельна одной из основных проекций прямой. На рис. 108 построено изображение прямой l (А, В) общего положения в системе плоскостей П1 _|_ П4, причем П4 || l. Новые линии связи A1A4 и В1В4проведены
перпендикулярно новой оси —П1/П4 параллельной горизонтальной проекции l1.
Новая проекция прямой дает истинную величину А4В4отрезка АВ (см. § 11) и позволяет определить наклон прямой к горизонтальной плоскости проекций (а = L1П1). Угол наклона прямой к фронтальной плоскости проекций (b = L1П2) можно определить, построив изображение прямой на другой дополнительной плоскости П4_|_П2 (рис. 109).
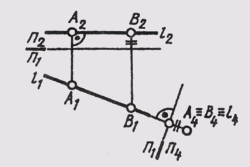
2. Преобразовать чертеж прямой уровня так, чтобы относительно новой плоскости проекций она заняла проецирующее положение.
Чтобы на новой плоскости проекций изображение прямой было точкой (см. § 10), новую плоскость проекций нужно расположить перпендикулярно данной прямой уровня. Горизонталь будет иметь своей проекцией точку на плоскости П4_|_ П1. (рис. 110), а фронталь f— на П4_|_ П2
Если требуется построить вырожденную в точку проекцию прямой общего положения, то для преобразования чертежа потребуется произвести две последовательные замены плоскостей проекций. На рис. 111 исходный чертеж прямой l (А,В) преобразован следующим образом: сначала построено изображение прямой на плоскости П4_|_ П2, расположенной параллельно самой прямой l. В системе плоскостей П2_|_ П4, прямая заняла положение линии l уровня (А2А4 _|_П2/П1;
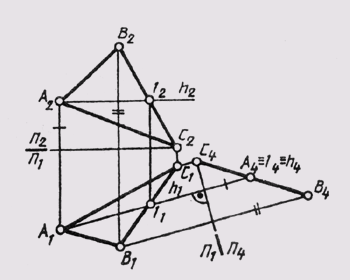
П4 _|_П5, причем вторая новая плоскость проекций П5 перпендикулярна самой прямой l. Так как точки А и В прямой находятся на одинаковом расстоянии от плоскости П4, то на плоскости П5 получаем изображение прямой в виде точки (А5 = B5 = l5).
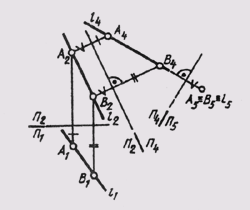
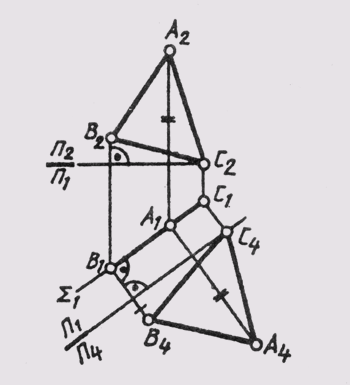
3. Преобразовать чертеж плоскости общего положения так, чтобы относительно новой плоскости она заняла проецирующее положение.
Для решения этой задачи новую плоскость проекций нужно расположить перпендикулярно данной плоскости общего положения и перпендикулярно одной из основных плоскостей проекций. Это возможно сделать, если учесть, что направление ортогонального проецирования на новую плоскость проекций должно совпадать с направлением соответствующих линий уровня данной плоскости общего положения. Тогда все линии этого уровня на новой плоскости проекций изобразятся точками, которые и дадут «вырожденную» в прямую проекцию плоскости (см. § 47).
На рис. 112 дано построение нового изображения плоскости 0 (ABC) в системе плоскостей П4 _|_П1. Для этого в плоскости 0 построена горизонталь h(A, 1), и новая плоскость проекций П4 расположена перпендикулярно горизонтали h. Графическое решение третьей исходной задачи приводят к построению изображения плоскости в виде прямой линии, угол наклона которой к новой оси проекции П1/П4, определяет угол наклона а плоскости Q(ABC) к горизонтальной плоскости проекций (а = Q ^ П1).
Построив изображение плоскости общего положения в системе П2 _|_П4, (П4 расположить перпендикулярно фронтали плоскости),
можно определить угол наклона Р этой плоскости к фронтальной плоскости проекций.
4. Преобразовать чертеж проецирующей плоскости так, чтобы относительно новой плоскости она заняла положение плоскости уровня.
Решение этой задачи позволяет определить величину плоских фигур.
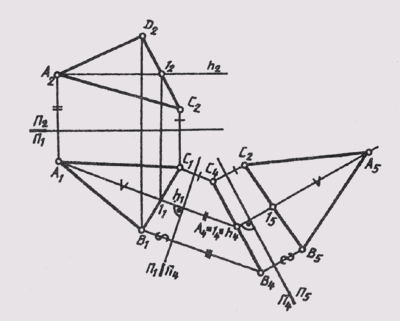
Новую плоскость проекций нужно расположить параллельно заданной плоскости. Если исходное положение плоскости было фронтально проецирующим, то новое изображение строят в системе и П2 _|_П4, а если горизонтально проецирующим, то в системе П1 _|_П4. Новая ось проекций будет расположена параллельно вырожденной проекции проецирующей плоскости (см. § 47). На рис. 113 построена новая проекция А4В4С4горизонтально проецирующей плоскости Sum (ABC) на плоскости П4 _|_П1
Если в исходном положении плоскость занимает общее положение, а нужно получить изображение ее как плоскости уровня, то прибегают к двойной замене плоскостей проекций, решая последовательно задачу 3; а затем задачу 4. При первой замене плоскость становится проецирующей, а при второй — плоскостью уровня (рис. 114).
В плоскости А(DEF) проведена горизонталь h (D — 1). По отношению к горизонтали проведена первая ось П1 / П4 _|_h1. Вторая новая ось
проекций параллельна вырожденной проекции плоскости, а новые линии связи — перпендикулярны вырожденной проекции плоскости. Расстояния для построения проекций точек на плоскости П5 нужно замерить на плоскости П1от оси П1 / П2и откладывать по новым линиям связи от новой оси П4 /П5. Проекция D5E5F5треугольника DEF конгруэнтна самому треугольнику ABC.
С применением способа замены плоскостей можно решать ряд других задач как самостоятельных, так и отдельных частей задач, включающих большой объем графических решений.
Источник
Начертательная геометрия, решение задач №6 и 8 ОмГУПС
>>>Назад к решению задачи №5
З а д а ч а 6
Определить натуральную величину треугольника AВС.
Задача решается способом замены плоскостей проекций, с использованием третьей и четвертой задач на преобразование: плоскость общего положения преобразуется в плоскость проецирующую, а плоскость проецирующая – в плоскость уровня.
Пусть плоскость общего положения задана треугольником АВС. Чтобы преобразовать эту плоскость в проецирующую, необходимо ввести новую плоскость проекций, перпендикулярную плоскости треугольника АВС, однако на комплексном чертеже это можно выполнить в том случае, если построить плоскость проекций перпендикулярно линиям уровня или следам плоскости. С этой целью проведем в плоскости треугольника АВС горизонталь. Перпендикулярно h1 начертим координатную ось х14 (П1/П4). Из проекции вершин треугольника А1, В1, С1 проведем линии связи и от оси х14 (П1/П4)
Таким образом, плоскость общего положения преобразована в плоскость проецирующую. Угол a между проекцией треугольника А4В4С4 и координатной осью является углом наклона плоскости треугольника АВС к плоскости П1.
Для преобразования проецирующей плоскости в плоскость уровня (решение четвертой задачи на преобразование) необходимо построить новую плоскость проекций параллельно проекции треугольника А4В4С4, провести линии связи и отложить координаты точек, взятые из плоскости П1 (от оси х1 системы П1/П4), от оси х2 системы П4/П5. Проекция треугольника А5В5С5 является натуральной величиной треугольника АВС.
З а д а ч а 8
Определить расстояние от точки D до плоскости треугольника ABC.
Искомое расстояние измеряется длиной перпендикуляра, опущенного из данной точки D на заданную плоскость. Этот перпендикуляр проецируется в натуральную величину на ту плоскость проекций, относительно которой данная плоскость является проецирующей, поэтому решение задачи может быть сведено к преобразованию, в результате которого заданная плоскость станет проецирующей, т. е. решают третью задачу на преобразование.
Чертежи высылаются, сразу после оплаты на карту Сбербанка, Яндекс.Деньги или Киви кошелек, в формате *.cdw (Компас)+рисунки jpeg в цвете в хорошем разрешении 300dpi. По желанию, могу заполнить штампы. Выполнение карандашом таких чертежей на заказ — от 1300 руб. в зависимости от варианта.
Источник