Определить натуральную величину треугольника авс способом вращения вокруг линии уровня

Метод вращения вокруг оси

Одним из наиболее эффективных методов определения метрических характеристик плоских фигур является вращение вокруг оси, в качестве которой обычно используют линию уровня или проецирующую прямую.

Способ вращения вокруг проецирующей прямой

Перемещение точки при её вращении вокруг проецирующей прямой является частным случаем параллельного перемещения и подчиняется следующим правилам.

1. Траектория движения точки – дуга окружности с центром, расположенным на оси вращения. Радиус окружности равен расстоянию между точкой и осью вращения.
2. При вращении точки вокруг прямой, перпендикулярной фронтальной плоскости проекции, фронтальная проекция точки перемещается по дуге окружности, а горизонтальная – параллельно оси X.
3. При вращении точки вокруг прямой, перпендикулярной горизонтальной плоскости проекции, горизонтальная проекция точки перемещается по дуге окружности, а фронтальная – параллельно оси X.

Руководствуясь рассмотренными правилами, повернем отрезок CD в положение, параллельное фронтальной плоскости проекции. В качестве оси вращения i будем использовать горизонтально проецирующую прямую, проведенную через точку D.

При повороте отрезка положение точки D не изменится, поскольку она лежит на оси i. Точку C’ переместим по дуге окружности радиусом C’D’ в положение C’₁ так, чтобы выполнялось условие C’₁D’₁ || X. Для нахождения точки C»₁ из C» проведем прямую, параллельную оси X, до пересечения её с линией связи, восстановленной из т. C’₁.

На следующем рисунке показан способ перевода отрезка в горизонтально проецирующее положение. Построения выполнены в два этапа и описаны ниже.

Сначала вращением вокруг оси i₁ CD перемещают в положение C₁D₁, параллельное фронтальной плоскости проекции. После этого вращением вокруг оси i₂ отрезок переводится в искомое положение C₂D₂, где он перпендикулярен горизонтальной плоскости проекции.

Расположение осей вращения выбирают исходя из удобства дальнейших построений. В нашей задаче горизонтально проецирующая прямая i₁ проходит через точку D, а проекция i»₂ фронтально проецирующей прямой i₂ лежит на продолжении отрезка C»₁D»₁.

Способ вращения вокруг линии уровня

Действенным и наиболее рациональным приемом решения задач, в которых требуется определить натуральную величину угла, является способ вращения вокруг линии уровня.

Основные правила построения

1. Радиус вращения точки равен расстоянию между точкой и линией уровня, выполняющей роль оси. Натуральную величину радиуса определяют методом прямоугольного треугольника.
2. При вращении вокруг горизонтали h точка перемещается по окружности, которая проецируется на горизонтальную плоскость в отрезок прямой, перпендикулярный горизонтальной проекции горизонтали h’. На фронтальную плоскость окружность, по которой движется точка, проецируется в эллипс. Строить его нет необходимости.
3. При вращении вокруг фронтали f точка перемещается по окружности, которая проецируется на фронтальную плоскость в отрезок прямой, перпендикулярный фронтальной проекции фронтали f». Вместе с тем горизонтальная проекция линии перемещения представляет собой эллипс, строить который не обязательно.

Рассмотрим, как определить действительную величину угла между прямыми a и b, пересекающимися в точке A. Построения представлены на рисунке и выполнены согласно алгоритму, который описан ниже.

1. Проводим фронтальную проекцию h» горизонтали h. Она пересекает прямые a» и b» в точках 1» и 2». Определяем горизонтальные проекции 1′ и 2′ и через них проводим h’.
2. Находим центр вращения O. Его горизонтальная проекция O’ лежит на пересечении прямой h’ с перпендикуляром, проведенным из A’ к h’.
3. Определяем натуральную величину радиуса вращения R = O’A’₀. Для этого строим прямоугольный треугольник O’A’A’₀, катет которого A’A’₀ равен расстоянию от A» до h».
4. Проводим дугу окружности радиусом R до пересечения её с прямой O’A’ в точке A’₁. Соединяем A’₁ с точками 1′ и 2′. Искомый угол ϕ построен.

Источник

СПОСОБ ВРАЩЕНИЯ ВОКРУГ ЛИНИИ УРОВНЯ

Способ вращения вокруг линий уровня используется в начертательной геометрии главным образом для определения натуральных величин плоских фигур.

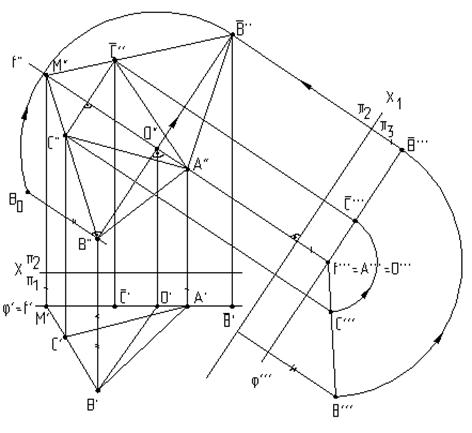
На рис.6.11 приведен пример определения натуральной величины треугольника АВС. Это решение равносильно решению четвертой основной задачи на преобразование комплексного чертежа и состоит в следующем:

Во-первых, в плоскости заданного треугольника проводится линия уровня, например, фронталь, вокруг которой нужно повернуть заданную фигуру до положения, параллельного фронтальной плоскости проекций, или совместить эту фигуру с плоскостью j, проходящей через выбранную линию уровня — фронталь f.

Во-вторых, поворот можно осуществить преобразовав заданную плоскую фигуру — треугольник АВС — в проецирующую плоскость, введя дополнительную плоскость проекций p₃, перпендикулярную фронтали f. Эта плоскость пересечет плоскость проекций p₂ по оси х₁. Проецируя треугольник АВС на эту плоскость, получим прямую А”’C”’B”’. Аналогично решению на рис.6.10, плоскость треугольника А”’C”’B”’можно преобразовать в плоскость уровня относительно фронтальной плоскости проекций p₂, повернув вокруг фронтали f D А”’C”’B”’до положения 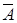«`«`«`. 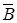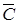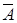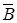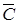При этом горизонтальная проекция треугольника ``` совпадет с горизонтальной проекцией фронтали. Треугольник АВСспроецируется на p₂ в истинную величину. Плоскость треугольника совместилась с j«.

Но задача может быть решена без введения дополнительной плоскости проекций p₃, так как натуральную величину радиуса вращения точки В можно определить с помощью способа прямоугольного треугольника. Его применение показано на исходном чертеже и дополнительного пояснения не требует.

В случае задания плоскости ее следами, такую плоскость можно совместить с плоскостью проекций вращением вокруг соответствующего следа этой плоскости.

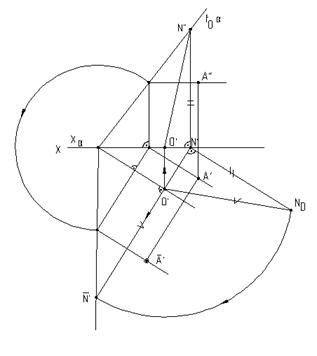
На рис.6.12 плоскость a(h_0aÇf_0a), заданная следами, совмещена с горизонтальной плоскостью проекций. Для нахождения совмещенного положения плоскости на ее фронтальном следе выбрана произвольная точка N(N«,N`) и из нее опущен перпендикуляр NO(N«O«,N`O`) на горизонтальный след плоскости. Дальнейшее построение аналогично решению задачи на рис.6.11.

При совмещении плоскости общего положения с плоскостью проекций может быть найдено совмещенное положение любой фигуры, принадлежащей этой плоскости, например, точки А.

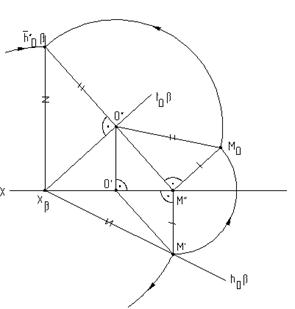
На рис.6.13 плоскость b(h_0bÇf_0b) cовмещена с плоскостью p₂. Построения аналогичны и понятны из чертежа. При этом построении точка М(М«,M`) выбрана на горизонтальном следе плоскости, так как совмещение происходит путем вращения плоскости вокруг фронтального следа f_0b плоскости b.

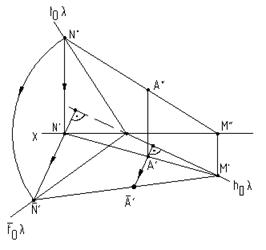
На рис. 6.14 приведен пример совмещения тупоугольной плоскости l с горизонтальной плоскостью проекций. Совмещенное положение 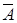` точки А , принадлежащей заданной плоскости, найдено с помощью вспомогательной прямой MN.

Фролов С.А. Начертательная геометрия. М.: “Машиностроение”, 1983., гл.II, 10,11,12.

Гордон В.О. и др. Курс начерт. геом. Изд. “Наука”, М.: Глава V,  34, 37.

Локтев В.О. Краткий курс начерт.геом. М.: Гл.VII, 22.

Источник

Определить натуральную величину треугольника ABC

Здравствуйте!
Что такое натуральная величина треугольника и как определить натуральную величину треугольника АВС?
Очень нужны примеры.
Спасибо!

Разберем что такое натуральная величина треугольника и как определить натуральную величину треугольника АВС.
Задание определения натуральной величины плоской фигуры относят к метрическим задачам.
Натуральную величину треугольника на эпюре Монжа можно определить несколькими способами. Рассмотрим некоторые из них.

1. Способ прямоугольного треугольника

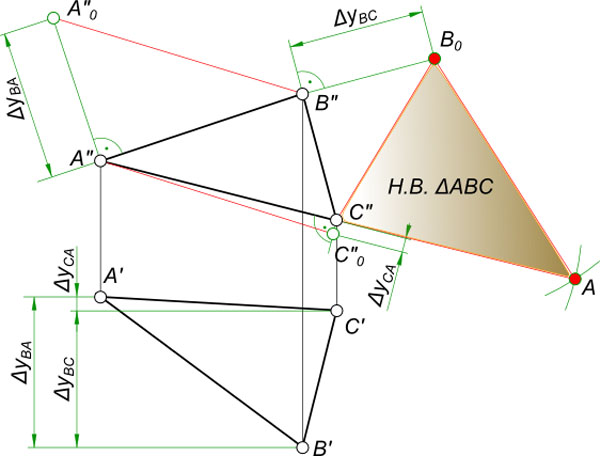
Необходимо поочередно применять этот способ, чтобы определить действительные величины отрезков, которые составляют треугольник, а далее методом засечек к одному из них строят два других.
Коротко о способе прямоугольного треугольника:
Данный способ применяют, чтобы определить натуральные величины отрезков и углов наклона этих отрезков к плоскостям проекций. Для этого нужно выполнить построение прямоугольного треугольника, один катет которого будет одной из проекций отрезка. Другой катет будет разностью глубин или высот конечных точек отрезка, а гипотенуза будет натуральной величиной.

1. Плоскопараллельное перемещение

1. Вращение вокруг перпендикулярных к плоскостям проекций осей

http://ru.solverbook.com/img_questions/16.02__15_1.jpg

1. Способ вращения вокруг горизонтали, являющихся линиями уровня

или вокруг фронтали, являющихся линиями уровня

1. Способ вращения вокруг следа (или совмещение с плоскостью проекций)

1. Способ перемены плоскости проекции

Источник

Определение натуральной величины треугольника АВС методом вращения вокруг линии уровня Вариант 1. Линия уровня (горизонталь h) проведена внутри плоскости. — презентация

Презентация была опубликована 6 лет назад пользователемЭдуард Касагов

Похожие презентации

Презентация на тему: » Определение натуральной величины треугольника АВС методом вращения вокруг линии уровня Вариант 1. Линия уровня (горизонталь h) проведена внутри плоскости.» — Транскрипт:

1 Определение натуральной величины треугольника АВС методом вращения вокруг линии уровня Вариант 1. Линия уровня (горизонталь h) проведена внутри плоскости треугольника АВС Вариант 2. Линия уровня (горизонталь h) проведена вне плоскости треугольника АВС

2 Х А2А2 В2В2 С2С2 С1С1 А1А1 В1В1 В 1 А 1 1 ВОВО О1О1 О2О h2h2 h1h1 Z Z 1 С 1 1. Строим h (h 2, h 1 ) из С С С 2. А 1 1, 1 h 1 ; В 1 1, 1 h 1, 1 h 1 О 1 О 2 О- центр вращения ОВ – радиус вращения О 1 В 0 — НВ ОВ 3. Строим В 1 4. В до пересечения с 1 А 1 5. А 1 В 1 С 1 НВ ( АВС) Вариант 1

3 Х h2h2 A2A2 C2C2 B2B2 В1В1 C1C1 А1А1 h1h1 А 1 В 1 С 1 В0В0 Z Z O1O1 O2O2 1 1 Вариант 2

Похожие презентации

Взаимное расположение прямой и плоскости. Признак параллельности прямой и плоскости. Математика, 10 класс.

Метрические задачи: определение натуральной величины длины отрезка, плоскости, угла наклона Способы нахождения: Метод замены плоскостей проекций; Вращение;

Некоторые следствия из аксиом. А А 1 А 1 B D C B1B1 C1C1 D1D1 ? ? ? Пересекает ли прямая ВА 1 с прямыми DD 1, АD 1 и DC?

Определение подобных треугольников Геометрия, 8 класс, Л.С. Атанасян Выполнила Сахарова М.А.

Две плоскости называются параллельными, если они не пересекаются. Определение II.

А А 1 А 1 а а А А 1 А 1. а А В С Построить А 1 В 1 С 1, симметричный АВС относительно прямой а. А 1 А 1 В 1 В 1 С 1 С 1 Как можно проверить равенство.

Отношение площадей треугольников, имеющих по равному углу. А В 1 В 1 А 1 А 1 С 1 С 1 С В Если угол одного треугольника равен углу другого треугольника,

А А 1 А 1 В В 1 В 1 С С 1 С 1 D D1D1 1) несколько точек, которые лежат в плоскости α. α Найдите:

2004 г Вар.1 В шар радиусом 0,511 вписана правильная треугольная призма АВСА 1 В 1 С 1. Прямая В 1 А образует с плоскостью ВСС 1 угол 45º. Найдите объем.

Определение 1: Треугольник – это геометрическая фигура, состоящая из трёх точек плоскости, не лежащих на одной прямой, соединённых отрезками. А В С Обозначение:

А 1 А 1 В 1 В 1 С 1 С 1 А 2 А 2 С 2 С 2 В 2 В 2 53 М Три отрезка А 1 А 2, В 1 В 2 и С 1 С 2, не лежащие в одной плоскости, имеют общую середину. Докажите,

Цилиндр Конус. Определение: Тело, ограниченное двумя кругами, расположенными в параллельных плоскостях и цилиндрической поверхностью, называется цилиндром.

Способ вращения вокруг оси, перпендикулярной плоскости проекций.

Угол между прямыми a b Пусть — тот из углов, который не превосходит любой из трех остальных углов. Тогда говорят, что угол между пересекающимися прямыми.

ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ Черевко В. Ю.

Задача 1 А В М С Стороны АВ и АС треугольника АВС лежат в плоскости. Докажите что и медиана лежит в этой плоскости.

ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ. Линия пересечения Линия пересечения распадается на две отдельные кривые Полное (проницание) – все образующие.

III признак равенства треугольников по трем сторонам. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то.

Умножение вектора на число Произведением вектора на число t называется вектор, длина которого равна, а направление остается прежним, если t>0, и меняется.

Сторона основания правильной треугольной призмы равна 8 см, боковое ребро равно 6 см. Найдите площадь сечения, проходящего через сторону верхнего основания.

Источник