Определить натуральную величину треугольника авс способом перемены плоскостей

Определить натуральную величину треугольника

— можно по ортогональной проекции, относительно которой, плоскость треугольника параллельна.

Замена плоскостей проекций

Построение натуральной величины треугольника методом замены плоскостей — в общем случае, исходные плоскости П₁/П₂ переведены в П₅/П₄, так что плоскость исходного треугольника параллельна П₅, а собственно треугольник проецируется в равный себе, так как каждый отрезок (сторона) треугольника параллельна плоскости проекций.

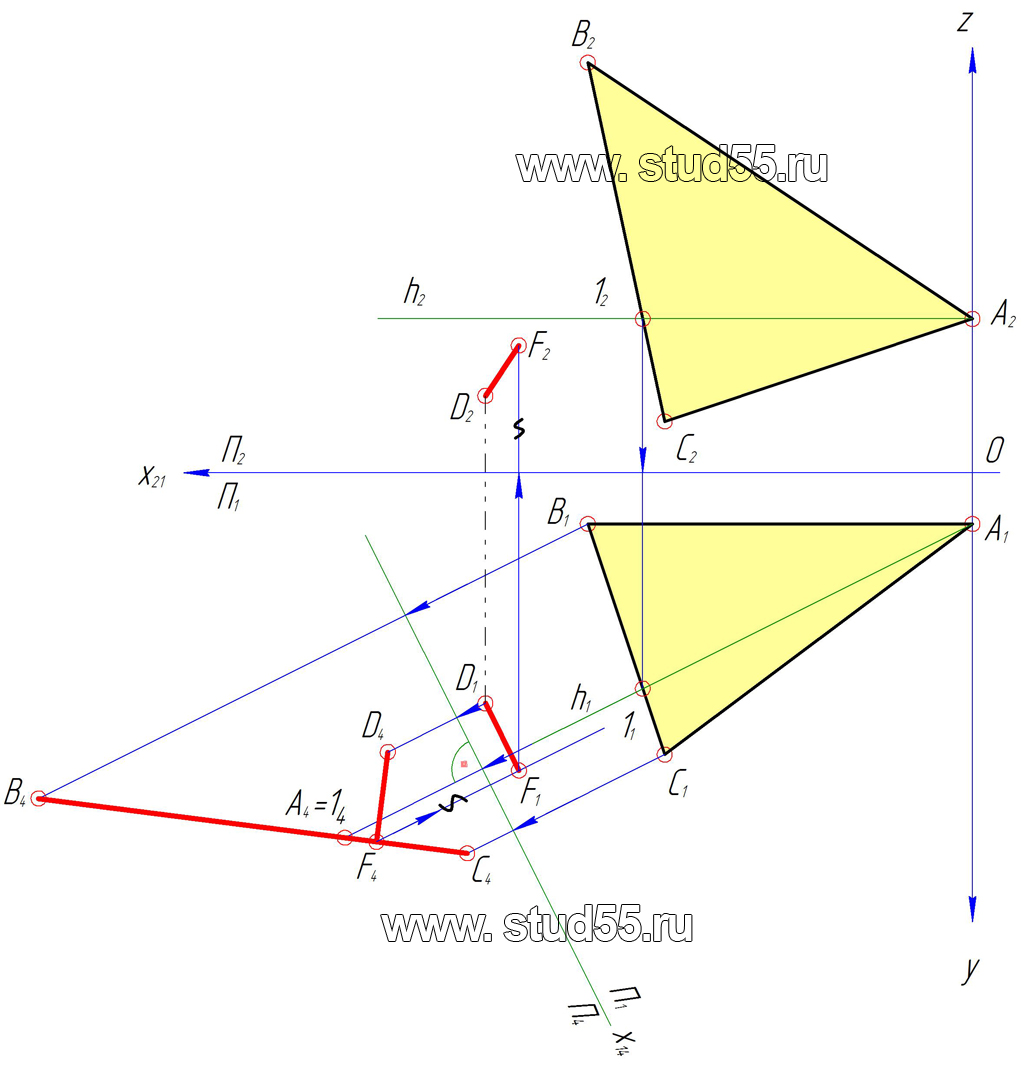
1. На горизонтальной проекции, в треугольнике ABC проведена фронталь f=AF (A₁F₁║OX).
2. Фронтальная проекция f₂ определена по проекционной связи F₁F₂ с условием F₂∈B₂C₂.
3. Замена П₁ на П₄⊥f — в результате ABC занимает положение проецирующее на П₄. A₄B₄C₄ — проецируется в один отрезок, и угол φ соответствует углу наклона плоскости треугольника ABC к фронтальной плоскости проекций П₂.
4. П₅║ABC заменяет П₂. A₅B₅C₅=ABC — натуральная величина заданного треугольника.

Начальный выбор фронтали произволен, и возможно выбрать для решения задачи любую линию частного положения лежащую в плоскости треугольника: фронталь, горизонталь или профильную прямую.

Плоскопараллельное перемещение

Используюя способ плоскопараллельного перемещения, выполняется преобразование исходных проекций до положения треугольника параллельно одной из исходных плоскостей проекций.

1. Плоско-параллельное перемещение до положения f⊥П₁
   ∠γ — наклон плоскости треугольника к фронтальной плоскости проекции.
2. Приведение вращением вокруг фронтально проецирующей оси до ABC║П₂

R на первом этапе показывает эквивалентность плоскопараллельного перемещения и метода вращения.

Способ вращения вокруг фронтали

1. В плоскости треугольника выбрана горизонталь f=AF
2. Методом прямоугольного треугольника определён радиус R вращения точки C вокруг f.
3. |R|=|fC|=|f₂C 0
   2 | — максимальное удаление точки C от оси вращения, при котором плоскость треугольника занимает положение параллельное фронтальной плоскости проекций.
4. B 0
   2 определена как пересечение F₂C 0
   2 с перпендикуляром к фронтальной проекции оси вращения f₂

Аналогично, можно решить задачу определения натуральной величины треугольника вращением вокруг горизонтали или совмещением плоскости фигуры с горизонтальной плоскостью проекции вращением вкруг горизонтального следа плоскости.

Источник

Начертательная геометрия, решение задач №6 и 8 ОмГУПС

>>>Назад к решению задачи №5

З а д а ч а 6

Определить натуральную величину треугольника AВС.

Задача решается способом замены плоскостей проекций, с использованием третьей и четвертой задач на преобразование: плоскость общего положения преобразуется в плоскость проецирующую, а плоскость проецирующая – в плоскость уровня.

Пусть плоскость общего положения задана треугольником АВС. Чтобы преобразовать эту плоскость в проецирующую, необходимо ввести новую плоскость проекций, перпендикулярную плоскости треугольника АВС, однако на комплексном чертеже это можно выполнить в том случае, если построить плоскость проекций перпендикулярно линиям уровня или следам плоскости. С этой целью проведем в плоскости треугольника АВС горизонталь. Перпендикулярно h₁ начертим координатную ось х₁₄ (П₁/П₄). Из проекции вершин треугольника А₁, В₁, С₁ проведем линии связи и от оси х₁₄ (П₁/П₄)

Таким образом, плоскость общего положения преобразована в плоскость проецирующую. Угол a между проекцией треугольника А₄В₄С₄ и координатной осью является углом наклона плоскости треугольника АВС к плоскости П₁.

Для преобразования проецирующей плоскости в плоскость уровня (решение четвертой задачи на преобразование) необходимо построить новую плоскость проекций параллельно проекции треугольника А₄В₄С₄, провести линии связи и отложить координаты точек, взятые из плоскости П₁ (от оси х₁ системы П₁/П₄), от оси х₂ системы П₄/П₅. Проекция треугольника А₅В₅С₅ является натуральной величиной треугольника АВС.

З а д а ч а 8

Определить расстояние от точки D до плоскости треугольника ABC.

Искомое расстояние измеряется длиной перпендикуляра, опущенного из данной точки D на заданную плоскость. Этот перпендикуляр проецируется в натуральную величину на ту плоскость проекций, относительно которой данная плоскость является проецирующей, поэтому решение задачи может быть сведено к преобразованию, в результате которого заданная плоскость станет проецирующей, т. е. решают третью задачу на преобразование.

Чертежи высылаются, сразу после оплаты на карту Сбербанка, Яндекс.Деньги или Киви кошелек, в формате *.cdw (Компас)+рисунки jpeg в цвете в хорошем разрешении 300dpi. По желанию, могу заполнить штампы. Выполнение карандашом таких чертежей на заказ — от 1300 руб. в зависимости от варианта.

Источник

Определить натуральную величину треугольника ABC

Здравствуйте!
Что такое натуральная величина треугольника и как определить натуральную величину треугольника АВС?
Очень нужны примеры.
Спасибо!

Разберем что такое натуральная величина треугольника и как определить натуральную величину треугольника АВС.
Задание определения натуральной величины плоской фигуры относят к метрическим задачам.
Натуральную величину треугольника на эпюре Монжа можно определить несколькими способами. Рассмотрим некоторые из них.

1. Способ прямоугольного треугольника

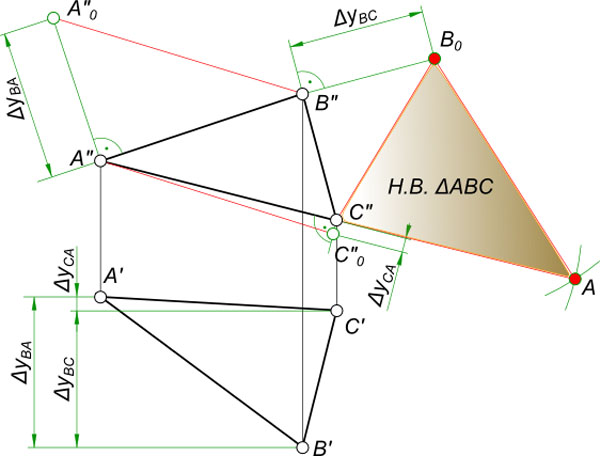
Необходимо поочередно применять этот способ, чтобы определить действительные величины отрезков, которые составляют треугольник, а далее методом засечек к одному из них строят два других.
Коротко о способе прямоугольного треугольника:
Данный способ применяют, чтобы определить натуральные величины отрезков и углов наклона этих отрезков к плоскостям проекций. Для этого нужно выполнить построение прямоугольного треугольника, один катет которого будет одной из проекций отрезка. Другой катет будет разностью глубин или высот конечных точек отрезка, а гипотенуза будет натуральной величиной.

1. Плоскопараллельное перемещение

1. Вращение вокруг перпендикулярных к плоскостям проекций осей

http://ru.solverbook.com/img_questions/16.02__15_1.jpg

1. Способ вращения вокруг горизонтали, являющихся линиями уровня

или вокруг фронтали, являющихся линиями уровня

1. Способ вращения вокруг следа (или совмещение с плоскостью проекций)

1. Способ перемены плоскости проекции

Источник

Чертежик

Метки

Натуральная величина треугольника с описанием.

Натуральная величина треугольника определяется 2 методами:

1. замена плоскостей проекции;
2. плоскопараллельное перемещение.

Это задание является обязательным для студентов в учебных заведениях и для его решения необходимо изучить тему: » Способы преобразования чертежа».

Для наглядности я использовал определенное задание и на его примере покажу как находится натуральная величина треугольника.

Алгоритм определения натуральной величины плоскости:

Замена плоскостей проекции

1.) Для построения чертежа использовал задание, расположенное снизу. Первоначально строятся точки по координат в плоскостях П1 и П2.

2.) Строится дополнительная горизонтальная линия 1 1 в верхнем изображении (проводится линия от средне расположенной точки по высоте), затем опускают дополнительные отрезки на нижнее изображение (как указано на рисунке снизу) и соединяют прямой. Эта прямая необходима для того, чтобы на ней расположить вспомогательную плоскость.

3.) Построив прямую на нижнем рисунке, чертится под углом 90 0 ось Х 1 (от точки С1 располагаем на произвольном расстоянии, но не слишком далеко). Затем отмеряются расстояния:

• от С2 до оси Х;
• от В2 до оси Х;
• от А0 до оси Х.

Полученные размеры откладываются от оси Х1 (размеры указаны разными цветами на рисунке снизу) и соединяют, далее подписываются точки.

4.) Строится еще одна дополнительная ось Х2, расположенная параллельно отрезку В 4 С 4 А 4. От точек В4,С4 и А4 проводят прямые перпендикулярные оси Х2.

5.) Отмеряются расстояния:

• от В1 до Х1;
• от С1 до Х1;
• от А1 до Х1.

Полученные результаты измерений откладываются от иси Х2 (на изображении снизу отмечены зелеными и голубым цветами).

6.) Соединяются точки и подписывают полученную плоскость заглавными «Н.В.»

Плоскопараллельное перемещение

7.) Откладывается отрезок на оси Х (обозначен синим цветом).

8.) Переносятся точки на текущее построение.

9.) Соединяют точки, получившиеся при переносе из плоскостей проекций. 10.) Методом вращения точки А2′, С2′ переносятся на горизонтальную прямую, а точка В2′ не меняет свое положение (относительно ее и происходило вращение).11.) Откладывается точка (располагают от оси Х на небольшом расстоянии, т.е. произвольном), относительно которой и будет откладываться плоско параллельное перемещение плоскости. 12.) От точек А2′, С2′ и В2′ опускаются прямые. Далее циркулем необходимо отмерить расстояния:

Затем эти размеры откладываются от С1′ (обозначены красным и синим цветами).

13.) Соединяются и подписываются точки (А1′, В1′ и С1′). Опускают прямые от С2″ и А2″14.) От точек С1 и А1 отводят прямые до пересечения с прямыми опущенными от точек С2″ и А2″. В месте пересечения ставится точка.15.) Завершающим шагом является соединение точек и обводка линиями всего чертежа.Пример чертежа на тему «Натуральная величина треугольника» смотрите здесь.

Источник