Определить координаты центра тяжести плоской фигуры аналитическим способом

Определение центра тяжести плоской фигуры
методическая разработка

Определение центра тяжести плоской фигуры. В разработке указан способ определения центра тяжести аналитическим образом. Разработка будет полезна студентам для осовения практических умений по дисциплине «Техническая механика».

Скачать:

Вложение	Размер
metodicheskaya_razrabotka_tsentr_tyazhesti_ploskoy_figury.docx	165.39 КБ

Предварительный просмотр:

Определение центра тяжести плоской фигуры

Центр тяжести применяется при исследовании устойчивости положений равновесия тел и сплошных сред, находящихся под действием сил тяжести и в некоторых других случаях, а именно: в сопротивлении материалов и в строительной механике – при использовании правила Верещагина.

При определении координат центра тяжести используются следующие методы:

1) метод симметрии: если сечение имеет центр симметрии или ось симметрии, то центр тяжести находится в центре симметрии или на оси симметрии;

2) метод разделения: сложные сечения разделяем на несколько простых частей, положение центров тяжести которых, легко определить;

3) метод отрицательных площадей: этот способ является частным случаем способа разделения. Он используется, когда сечение имеет вырезы, срезы, полости (отверстия), которые рассматриваются как часть сечения с отрицательной площадью.

При решении задач на определение центра тяжести сложных сечений следует придерживаться следующего порядка:

1. Выбрать метод, который наиболее применим к данной задаче.

2. Разбить сложное сечение на простые части, для которых центры тяжести известны.

3. Выбрать оси координат. При этом необходимо помнить, что: если тело имеет плоскость симметрии, то его центр тяжести лежит в этой плоскости; если тело имеет ось симметрии, то его центр тяжести лежит на этой оси; если тело имеет центр симметрии, то его центр тяжести совпадает с центром симметрии.

4. Определить координаты центров тяжести отдельных частей относительно выбранных осей.

5. Используя формулы определить искомые координаты центра тяжести заданного сечения.

=

где А 1 , А 2 . Аn — площади простых сечений;

x 1 , x 2 … x n , y 1 , y 2 … y n – координаты центра тяжести простых сечений.

Координаты центра тяжести сложной плоской фигуры определяются после разделения ее на простые фигуры и определения их центров тяжести.

Координаты центра тяжести некоторых простых плоских фигур:

Порядок выполнения задания:

1) начертить заданное сложное сечение (фигуру), выбрать оси координат.

2) разбить сложное сечение на простые, для которых центры тяжести и силы тяжести известны;

3) определить необходимые данные для простых сечений:

4) определить координаты центров тяжести простых сечений относительно выбранных осей координат;

5) определить положение центра тяжести сложного сечения.

Найти координаты центра тяжести плоской фигуры, изображенной на рисунке.

Выбираем оси координат так, чтобы нижний и левый край фигуры совпали с ними:

Делим заданную плоскую фигуру на прямоугольник (1), треугольник (2) и круг (3).

Вычисляем площади этих фигур:

S 1 = 10·20 = 200; S 2 = 0,5·5·10 = 25; S 3 = π·9 =28,3.

Определяем координаты центров тяжести фигур:

x 2 = 5; y 2 = 11,7.

Координаты центра тяжести всей плоской фигуры:

По теме: методические разработки, презентации и конспекты

Проецирование плоских фигур

Методическая разработка по теме Проецирование плоских фигурпо дисциплине инженерная графика. Краткое содержание материала, тестовое задание по теме, задание на графическую работу.

Методическая разработка «Сценарий интегрированного занятия Математика + Информатика «Вычисление площади плоской фигуры с помощью определенного интеграла»

Интегрированный урок — это учебное занятие, на котором тема рассматривается с различных точек зрения, средствами нескольких дисциплин. Интегрированные уроки формируют познавательный интерес обучающихс.

Методическая разработка урока по технической механике «Определение центра тяжести плоской фигуры»

Данная методическая разработка содержит методические указания по проведению лабораторной работы «Определение центра тяжести плоской фигуры».

План — конспект урока на тему Центр тяжести для студентов СПО

ГБПОУ «Навашинский политехнический техникум», Россия, Глебова Ю.В., 2012 г., 12 стр., 76 слайдов; Описание: План-конспект урока по дисциплине «Техническая механика» на тему «Центр тяжести» для студент.

Творческая работа студента «Роль центра тяжести в машиностроении»

ГБПОУ «Навашинский судомеханический техникум»; Выполнил: Кирилов А.В. студент II курса; Руководитель: Глебова Ю.В.,преподаватель ; Исследовательская работа — 26 стр., , 2014 г. Практ.

Методические указания по выполнению лабораторной работы «Определение положения центра тяжести сечения» по дисциплине «Техническая механика»

МИНИСТЕРСТВО ОБРАЗОВАНИЯ НИЖЕГОРОДСКОЙ ОБЛАСТИГосударственное бюджетное профессиональное образовательное учреждение «Кстовский нефтяной техникум имени Бориса Ивановича Корнилова»ОП-04Система.

Определение центра тяжести плоских фигур

решени задач на определение центра тяжести плоских фигур.

Источник

Определение центра тяжести сложной плоской фигуры.

Положение центра тяжести сложной плоской фигуры определяется координатным способом по следующему правилу:

1. Сложная фигура разбивается на составные части, представляющие собой простые геометрические фигуры. При этом желательно, чтобы количество составных частей было минимальным.
2. Определяются площади составных частей. При этом необходимо помнить, что площадь вырезанной фигуры считается отрицательной.
3. Выбирается система координат, связанная с заданной фигурой, обозначаются на чертеже центры тяжести составных частей и определяются их координаты в выбранной системе координат.
4. Определяются координаты центра тяжести всей фигуры по формулам:

, где

— координаты центров тяжести составных частей;

— площади составных частей.

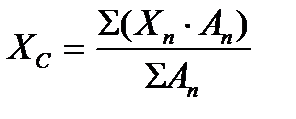
Удобно результаты занести в таблицу

5. По полученным координатам обозначается на чертеже фигуры её центр тяжести.

Примеры решения задачи.

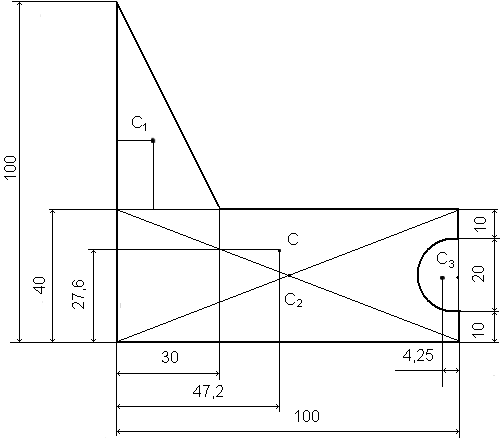
ПРИМЕР 1. Сложная фигура состоит из простых геометрических фигур (рисунок 23).

Рисунок 23. Сложная плоская фигура.

1. Разбиваем заданную плоскую фигуру на простые составные части:

1- прямоугольный треугольник, 2- прямоугольник, 3- круговой сектор (вырезан).

2. Определяем площади каждой составной части:

Площадь прямоугольного треугольника равна половине произведения его катетов.

мм 2 .

Площадь прямоугольника равна произведению его сторон:

мм 2 .

Площадь кругового сектора, представляющего половину круга, равна:

мм 2 .

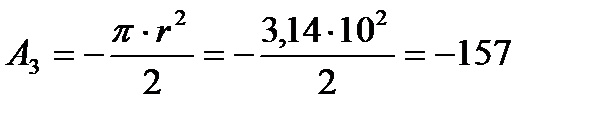
3. Выбираем систему координат так, чтобы вся фигура расположилась в первой координатной четверти. Обозначим на чертеже фигуры центры тяжести составных частей (рисунок 19) и определим их координаты:

мм, мм — координаты центра тяжести треугольника.

мм, мм — координаты центра тяжести прямоугольника.

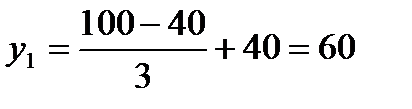
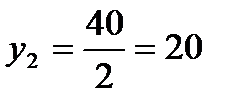
Фигура	Xn мм.	Yn мм.	An мм 2
Треугольник	10	60	900
Прямоугольник	50	20	4000
Сектор(вырез)	95,75	20	-157

мм., мм. — координаты центра тяжести кругового сектора.

4. Определяем координаты центра тяжести всей фигуры:

мм.

мм.

5. По полученным координатам обозначаем центр тяжести всей фигуры на её чертеже (рисунок 20).

Задача для самостоятельного решения. Определить координаты центра тяжести плоской фигуры, указанной на рисунке 24. Первые 10 вариантов решают задачу для 1 фигуры, следующие (с 11 по 20) – для 2 фигуры, следующие (с 21 по 30) – для 3 фигуры.

Х

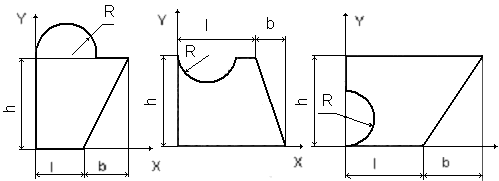
Рисунок 24. Сложные фигуры для задания 1.6 (пример1)

Таблица 6. Размеры элементов сложной фигуры для задания 1.6 (пример 1).

1	2	3	4	5	6	7	8	9	10
R, мм	10	20	15	25	30	28	24	22	18	16
h, мм	50	60	40	80	80	70	90	60	50	40
l, мм	60	50	50	60	60	80	70	80	80	60
b, мм	20	10	10	20	20	30	40	30	30	40

ПРИМЕР 2. Сложная фигура состоит из фасонных прокатных профилей (рисунок 25).

Рисунок 25. Сложная фигура, состоящая из прокатных профилей.

При решении этой задачи следует использовать сортамент на прокатные профили двутавры, швеллеры, уголки (таблицы 23, 24, 25). Решение задачи аналогичное решению предыдущей.

1. Разбивать заданную сложную фигуру на простые составные части не надо, так как она уже разбита на двутавр №24, швеллер №18, равнобокий уголок №9.

2. Определим по сортаментам на фасонные прокатные профили площади составных частей: площадь двутавра №24 см 2 (таблица 23), площадь швеллера №18 см 2 (таблица 24), площадь равнобокого уголка №9 см 2 (таблица 25).

3. Выбираем систему координат, обозначаем положения центров тяжести составных частей и определяем их координаты в выбранной системе координат в сантиметрах:

см -координаты центра тяжести двутавра №24.

см., см- координаты центра тяжести швеллера №18.

см., см. — координаты центра тяжести равнобокого уголка №9.

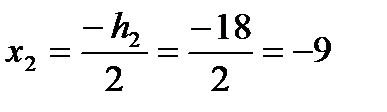
4. Определяем координаты центра тяжести всей фигуры по формулам:

см.

см.

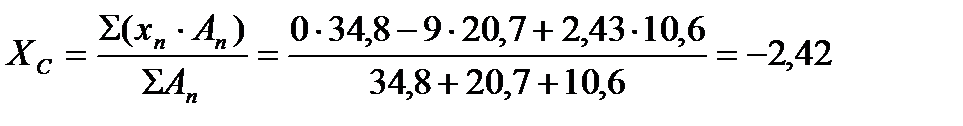
6. По полученным координатам обозначаем центр тяжести сложной фигуры на её чертеже (рисунок 25).

Задача для самостоятельного решения. Определить координаты центра тяжести фигуры, указанной на рисунке 26. Первые 10 вариантов выполняют решение для 1 фигуры, следующие (с 11 по 20) – для 2 фигуры, следующие (с 21 по 30) – для 3 фигуры.

.Рисунок 26. Сложные фигуры для задания 1.6 (пример 2)

Таблица 7. Номера профилей для задания 1.6. (пример 2)

Источник