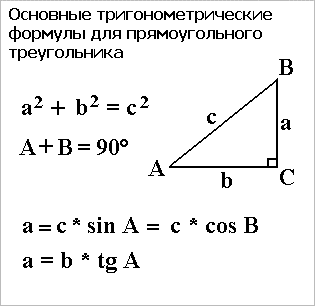Определение высоты разными способами

% способов определения высоты предметов

Определение высоты некоторых предметов

Рекомендуем несколько способов, при помощи которых можно определить высоту предметов.

1. По тени. В солнечный день можно определить высоту предмета по его тени, руководствуясь следующим правилом: высота измеряемого предмета во столько раз больше высоты известного вам предмета (палки, удочки), во сколько раз тень от измеряемого предмета больше тени от палки, удоччки.

Если при измерении окажется, что тень от палки или удочки в 2 раза больше длины палки или удочки, то высота измеряемого предмета будет в 2 раза меньше длины его тени, а если тень от палки или удочки будет равна их длине, высота измеряемого предмета также равна высоте своей тени.

2. При помощи равнобедренного треугольника. Приближаясь к предмету (например, к дереву) или удаляясь от него, установить треугольник у глаза так, чтобы один из его катетов был направлен отвесно, а другой совпал с линией визирования на вершину дерева. Высота дерева будет равняться расстоянию до дерева (в шагах) плюс высота до глаз наблюдателя.

3. По шесту. Взять шест, равный своему росту, и установить его на таком расстоянии от предмета (дерева), чтобы лёжа можно было видеть верхушку дерева на одной прямой с верхней точкой шеста.

Высота дерева будет равна расстоянию от головы наблюдателя до основания дерева.

4. При помощи высотомера со стрелкой. Изготовив прибор по данному чертежу, можно приступить к определению высоты какого-либо предмета. Находясь на различном расстоянии от предмета, надо следить, чтобы при визировании вершины дерева показания стрелки не выходили за пределы шкалы.

При визировании следует приложить глаз к отверстию сбоку прибора и, наклонив прибор, добиться, чтобы вторая визирная точка (угол на другом конце прибора) совпала с вершиной визируемого предмета. Стрелка укажет число, на которое следует умножить расстояние до предмета, чтобы получить его высоту. К этому прибавляется выста прибора во время визирования.

5. При помощи лужи. Если недалеко от дерева находится лужа, надо стать так, чтобы она помещалась между вами и предметом, а затем при помощи горизонтально положенного зеркальца найти в воде отражение вершины деерва. Высота дерева будет во столько раз больше роста человека, во сколько раз расстояние от него до лужи больше, чем расстояние от лужи до наблюдателя.

Источник

Простые способы определения высоты дерева или любого другого предмета по тени, шесту, лужице или зеркалу, прямоугольному треугольнику.

В полевых условиях иногда бывает очень важно и полезно владеть простейшими прикладными способами измерений на местности. Например способами определения высоты дерева или любого другого предмета на местности.

Простые способы определения высоты дерева или любого другого предмета по тени, шесту, лужице или зеркалу, прямоугольному треугольнику.

Высоту дерева или любого другого предмета на местности очень просто можно определить по тени, шесту, лужице или зеркальцу, и прямоугольному треугольнику.

Способ определения высоты дерева или другого предмета по своему росту и длине тени.

Если на ровном месте измерить шагами длину своей тени, а затем длину тени, отбрасываемой деревом илипредметом, то искомую высоту легко вычислить из пропорции :

АК/ак = КЕ/ке

где АК — высота дерева (В), КЕ — тень дерева (D), ак — ваш рост (b), ке — ваша тень (d).

Например длина вашей тени d равна трем шагам, тень дерева D равна девяти шагам, то есть тень дерева длиннее вашей тени в три раза. Если принять ваш рост за 1,5 метра, то высота дерева будет В = 1,5 х 3 = 4,5 метра.

Способ определения высоты дерева или другого предмета по шесту и своему росту.

Этот же способ можно применить при пасмурной погоде, когда тени от предметов не видны. В этом случае для измерения нужно взятьшест, равный длине вашего роста. Шест этот надо установить на таком расстоянии от дерева, чтобы лежа можно было видеть верхушку дерева на одной прямой линии с верхней точкой шеста. Тогда высота дерева равна расстоянию от вашей головы до основания дерева, то есть АС = ВС.

Способ определения высоты дерева или другого предмета по лужице или зеркальцу.

По лужице, зеркальцу илигелиографу высоту дерева или любого другого предмета на местности, можно измерять следующим образом. Станьте так, чтобы лужица поместилась между вами и деревом (В). Найдите точку, из которой видна отраженная в воде вершина дерева. Измеряемоедерево будет во столько раз выше вас, во сколько расстояние от него до лужицы (ВО) больше расстояния от лужицы до вас (АО). Вместо лужицы также можно воспользоваться зеркальцем, положив его горизонтально так, чтобы увидеть вершину дерева.

Способ определения высоты дерева или другого предмета с помощью прямоугольного треугольника с двумя острыми углами по 45 градусов.

С помощью прямоугольного треугольника с двумя острыми углами по 45 градусов, высоту дерева или другогопредмета определяют так. Отходя от дерева на некоторое расстояние и прикладывая треугольник к глазам так, чтобы один из его катетов был параллелен оси дерева, второй — параллелен земной поверхности, а гипотенуза представляла собой линию визирования.

Затем добиваются такого положения, чтобы линия визирования прошла через вершину дерева. В этом случае высота дерева D равна расстоянию от наблюдателя до дерева и плюс рост наблюдателя.

По материалам книги «Карта и компас мои друзья».
Клименко А.И.

Источник

Исследовательская работа по математике «Измерение высоты здания разными способами»

Муниципальное бюджетное общеобразовательное учреждение

«Средняя школа № 10 г. Ульяновска»

Исследовательская работа по математике

Измерение высоты зданий

учащийся 8 класса

Фаткулова Нурания Нурмиевна-

Теоретическая часть …. …………………..4-7

На уроках геометрии, при изучении темы «Подобие треугольников», я узнал, что свойства подобных треугольников могут быть использованы при проведении различных измерительных работ на местности. Мы познакомились с двумя задачами: определение высоты предмета и расстояния до недоступной точки. После решения задач из учебника мне стало интересно, смогу ли я, используя свои знания, вычислить высоту здания нашей школы и для точности сравнить с реальными показаниями.

Моя тема актуальна , потому что, практическое использование знаний по данной теме усиливает интерес к математике и содействует развитию математических способностей, появляется возможность без каких- либо сложных технических устройств и приборов измерить расстояние до недоступной точки. Это удобно, безопасно, материально экономично и сокращает время измерительных работ.

Цель работы: научиться определять высоту зданий по тени здания, фотографии здания, количества лестниц, . в здании и выяснить, используя погрешность вычислений, наиболее точный способ.

Объект исследования: высота здания школы №10 на улице Вольная,6.

Предмет исследования: четырёхэтажное здание школы №10 на улице Вольная,6.

Для достижения цели нужно выполнить следующие задачи:

— по литературным и интернет — источникам найти способы определения высоты школы;

— провести соответствующие измерения на местности(тени и . );

— сбросить тело и засечь время его падения;

— узнать высоту здания из плана – схемы здания школы № 10;

— проанализировать и вычислить погрешность измерений;

— определить наиболее точный способ определения высоты здания.

Я выдвинул гипотезу : если я смогу измерить высоту здания, не используя специальных приборов, то, она будет правдива?

— поисковый метод с использованием научной и учебной литература , а также поиск необходимой информации в сети интернет;

— практический метод выполнения вычислений с применением тени здания, фотографии здания, количества ступенек в здании и времени полета тела из четвертого этажа здания;

— сравнение и анализ полученных в ходе исследования данных.

В ходе исследовательской работы я определил несколько способов, которые оказались для меня доступными:

Измерение высоты зданий с помощью фотографии: я сфотографировался на фоне здания школы, измерил свой рост и высоту школы на фотографии, зная свой реальный рост, определил высоту исследуемого здания школы.

Измерение высоты зданий с помощью тени: в солнечный день, стоя рядом со зданием школы, измерил свою тень и здания, зная свой рост, определил высоту здания.

Измерение высоты зданий с помощью подсчёта количества ступенек в здании.

Измерение высоты зданий с помощью физических законов: я сбросил тело из четвертого этажа здания, засек время падения тела, по формуле нашел высоту здания.

Измерение высоты зданий с помощью фотографии: я сфотографировался рядом со зданием школы, узнал сколько раз, я могу поместиться рядом со зданием, умножил это количество на мой рост, полученная высота является высотой здания.

Для выявления наиболее точного способа, я определил абсолютную погрешность моих вычислений.

Рассказывают, что египетский фараон Амазис приказал измерить высоту пирамиды Хеопса. Жрецы не знали, как выполнить эту задачу. И тогда им на помощь пришел Фалес. Собравшиеся у подножия пирамиды жрецы с интересом следили за действиями милетского мудреца, который очертил вокруг себя окружность, радиус которой был равен его росту. Фалес стал в центре окружности и стал дожидаться, когда конец его тени достигнет окружности. Когда это произошло, Фалес быстро направился к месту на земле, где заканчивалась тень пирамиды, и положил там камень. Фалес справедливо считал, что в этот момент и тень от пирамиды равна высоте самой пирамиды. Затем Фалес измерил расстояние от камня до подножия пирамиды, прибавил к этому расстоянию половину длины основания пирамиды и огласил результат своего труда.

Таким образом, можно измерить и высоту дерева. Но этот способ не всегда можно применить. Чтоб не дожидаться когда ваша тень станет равна вашему росту, можно поступить проще. Измерить тень дерева и вашу собственную. Во сколько раз тень дерева больше вашей тени, значит во столько же раз дерево выше вашего роста.

Определение и признаки подобия треугольников.

Подобные треугольники – это треугольники, у которых углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

Первый признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Второй признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

Третий признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Определение абсолютной погрешности

Абсолютная погрешность приближённого значения – это модуль разности точного и приближённого значений.

Примеры определения расстояний до недоступной точки.

Определение высоты тела по тени

В солнечный день не составляет труда измерение высоты предмета, предположим дерева, по его тени. Необходимо только, взять предмет (например, палку) известной длины и установить ее перпендикулярно поверхности. Тогда от предмета будет падать тень. Зная высоту палки, длину тени от палки, длину тени от предмета, высоту которого мы измеряем, можно определить высоту предмета. Для этого нудно рассмотреть подобие двух треугольников. Помните: солнечные лучи падают параллельно друг другу.

Определение высоты тела по зеркалу

Зеркало кладут горизонтально и отходят от него назад в такую точку, стоя в которой, наблюдатель видит в зеркале верхушку дерева. Луч света FD, отражаясь от зеркала в точке D, попадает в глаз человека. Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние от него до зеркала больше, чем расстояние от зеркала до вас. Помните: угол падения равен углу отражения (закон отражения).

Источник

Простые способы измерения расстояний и высот на местности

Прямые методы определения линейных расстояний

Точные измерения производятся с помощью мерной рулетки или стальной ленты, длиной 10 или 20 метров. Иногда, применяют длинный шнур (в виде толстого провода), на котором ставятся метки: белые – через каждые 2м и красные – через 10м, с закреплёнными, на концах, шпильками (стальными штырями или деревянными кольями). Важно, чтобы измерительные приспособления не растягивались и были точно отмерены, выверены по эталону.

При обмерах полей и промеров по извилистым контурам, на местности, до сих пор применяют полевой землемерный циркуль-измеритель «Ковылёк» (&quotдвухметровка&quot, старое название – «Сажень»), в виде буквы А. Это раскладывающаяся деревянная вилка, с постоянным раствором ножек, равным 2 метра.

Во время работ по топографической съёмке местности – ведут журнал измерений, составленный по стандартной форме, куда сразу заносятся номера точек стояния и результаты текущих измерений. Дополнительно, составляют, от руки – абрис (схематический чертёж снимаемой, в данный момент, местности).

Приблизительные, грубые измерения с невысокой точностью, производят шагомерно – парами своих шагов (равных, примерно, вашему росту, минус 10-20 сантиметров, в зависимости от темпа ходьбы, степени пересечённости местности и угла наклона земной поверхности). Результаты счёта – последовательно заносятся, записываются в блокнот, в виде таблицы данных для дальнейшего пересчёта пройденных дистанций и отрезков пути, в метры.

Спутниковые навигационные системы (для «гражданских» пользователей)

При измерении больших расстояний, могут помочь GPS-навигаторы (ориентировочная погрешность определения координат точки, при благоприятных условиях работы прибора – ±5–15 метров, в плане, т.е. на горизонтали). Высотомер грубоват – по абсолютной высоте, ошибка составит от ±10-50м до ±100-150 метров. При использовании смартфонных, мобильных приложений для навигации, погрешность измерений может быть больше, чем у специальных устройств. Максимально возможная точность достижима на многосистемных GPS-Glonass-Beidou приёмниках, при их работе на открытом пространстве, с достаточно ровным рельефом местности, если в это время нет сильных внешних помех, в виде магнитных бурь.

Дистанционные визуальные методы определения расстояний

Дистанционно-визуальные способы измерений длин – они применяются в тех случаях, когда существует непреодолимая преграда, препятствие (река, болото, озеро, глубокий овраг, горное ущелье), но сохраняется прямая видимость, достаточная для производства измерений.

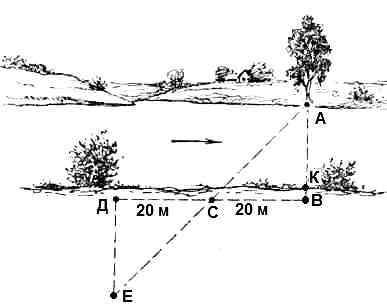
Ширину реки можно определить геометрическим глазомерным способом, путём построения вдоль её берега двух равных прямоугольных треугольников. Выбрав на противоположном берегу (в направлении, перпендикулярном руслу) какой-нибудь заметный предмет «А» (дерево, большой камень и т.п.), расположенный у самой кромки воды, вбивают напротив него колышек «В» (рисунок 1). Вдоль берега, перпендикулярно к линии АВ, отмеряют рулеткой или шагами, например 20м и вбивают колышек «С». На продолжении линии ВС в расстоянии, равном также 20 м, вбивают еще один колышек «Д». От колышка «Д» в направлении ДЕ, перпендикулярном (направления задаются при разведении рук в стороны и сведении их ладонями, прямо перед собой или с помощью крестообразного эккера) к линии ДВ, надо идти от реки до тех пор, пока колышек «С» не окажется на одной линии с предметом «А». Так как треугольники ABC и ЕДС абсолютно и полностью равны, то ширина реки будет равна расстоянию ДЕ минус ВК (интервал до уреза воды). Если плечи ДС и СВ не равны (нет возможности пройти вдоль берега; мешают густые заросли), то AB = DE*BC/CD

Рис.1

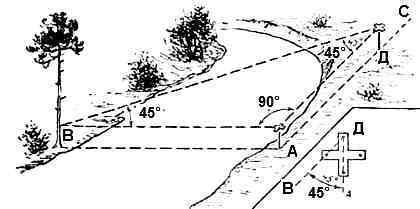
Определить ширину реки можно и не отходя от воды, построением на местности прямоугольного равнобедренного треугольника АДВ (рис. 2). Построив на точке «А» прямой угол, отходят в направлении АС до такой точки «Д», из которой предмет «В» будет засекаться под углом 45° (в этом случае, АВ=АД). Для разбивки углов применяется самодельный крестообразный эккер (в виде квадратного листа бумаги с загнутыми, кверху, уголками или, установленной на подставку, плоской деревянной крестовины с четырьмя вбитыми, по квадрату, шпильками), с помощью которого строят углы 45° и 90° от ходовой линии (основной магистрали). На точке «А», для лучшей её видимости при расстановке вешек в створе, ставится хорошо заметный «макет» (например, крепится белый лист бумаги, обращённый в сторону пункта «Д»).

Экспресс-метод, без установки эккера на штативе – две перекрещенных прямых веточки, одинаковой длины, держать горизонтально на уровне глаз так, чтобы одна ветка была параллельна течению реки и направлена на точку «А» (смотреть, прикрыв один глаз). Тогда, линия угла-сорокапятки, проходящая через концы веточек – смотрится-визируется закрыв другой глаз и слегка наклонив голову. Можно визировать и с помощью шкалы компаса, или оптического приспособления буссоли, или циферблата наручных часов (в качестве направляющей можно использовать измерительную линейку, прикладывая её ребром через центр лимба).

Имея возможность провести на местности триангуляцию (померить угломером или по лимбу компаса) и посчитать тангенс угла (в полевых условиях, это возможно проделать без калькулятора и точных математических таблиц Брадиса, при помощи транспортира, линейки и циркуля), можно визировать под любым углом, а затем – считать по формуле:
АВ = АД * tg АДВ .

Если угол равен 45 градусов, тогда tg(45°)=1 и, соответственно, АВ=АД
tg(64°) = 2 и АВ=АД*2
tg(72°) = 3 и АВ=АД*3

Рис.2

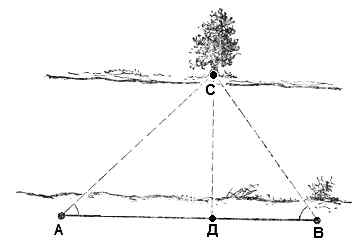
Достаточно точно ширина реки может быть установлена способом прямой засечки (рис. 3). Для этого на противоположном берегу выбирают приметный предмет «С», а вдоль берега, на котором находится исследователь, прокладывают базис АВ и измеряют длину его. Из точек «А» и «В» делают засечки на точку «С», т. е. измеряют углы CAB и ABC. Построив с помощью мерной линейки и транспортира треугольник ABC, можно получить в принятом для базиса АВ масштабе искомую ширину реки.

Тем же способом ширина реки может быть определена и без непосредственного измерения углов CAB и ABC, с помощью графических засечек на планшете. Надо отложить на бумаге длину базиса AB в выбранном масштабе, затем из концов базиса, ориентировав, стоя на угловых точках, планшетку, прочертить направления на какой-нибудь видимый предмет «С» противоположного берега. Тогда, ширину реки можно определить графически – на чертеже, пересчитав по его масштабу.

Рис.3

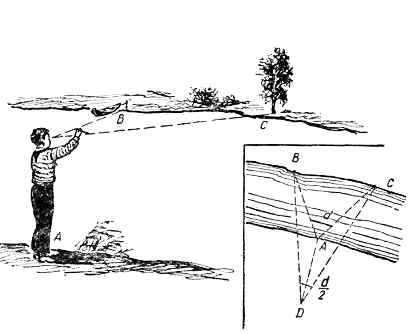
Весьма прост и удобен приближенный прием измерения ширины реки (или расстояния до недоступного объекта) при помощи травинки или нитки. Стоя на берегу реки в точке «А», замечают на противоположном ее берегу два приметных предмета (например лодку В и дерево «С»), расположенных близ уреза (рис. 4). Затем, взяв травинку (нитку) за ее концы вытянутыми перед собой руками, замечают ее длину «d», которой закрывается промежуток ВС между выбранными предметами (смотреть надо одним глазом). Затем, сложив травинку пополам, отходят от реки до тех пор (точка «D»), пока промежуток ВС не будет закрыт травинкой. Пройденное расстояние AD будет равно ширине реки.

Рис.4

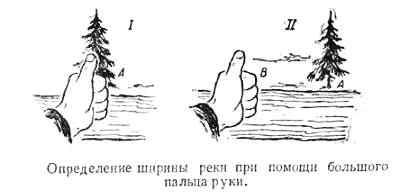
Существует и такой, самый быстрый, но весьма приближённый способ определения ширины реки – закрывают правый глаз и направляют поднятый вверх большой палец вытянутой горизонтально руки (рис. 5) в направлении приметного предмета «А» противоположного берега. Затем, поменяв открытый глаз (так появляется стереоскопический эффект в виде стереопары изображений из двух различных точек наблюдения), замечают, что палец как бы отскочил вбок от наблюдаемого предмета в точку «В». Оценив на глаз расстояние АВ, в метрах (предполагая, примерно, высоту или ширину предметов), и умножив его на 10, получают примерную ширину реки. Человек при таких измерениях – выступает как стереофотограмметрический прибор.

Рис.5

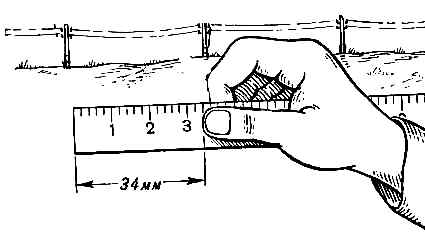
Определение расстояний по угловой величине известных предметов

Пример (рис. 6). Расстояние между телеграфными столбами линии связи, равное 55м (у старых, деревянных, обычно — 50-60 метров интервала, с высотой 6м от земли), покрывается 34 миллиметровыми делениями линейки (3.4см), удаленной от глаз на 50 сантиметров (рука вытянута прямо перед собой). Тогда, расстояние до телеграфной линии, по уравнению соотношения сторон подобных треугольников, равно:
Д = 55м * ( 50см / 3.4см ) = 809 м.

Если столбы видны не под прямым углом, а сбоку, тогда, чтобы исключить завышение расстояния до них – надо результат счёта умножить ещё и на поправочный коэффициент:
для 45 градусов – 0.7
30° – 0.9

Например, для рассмотренного примера, при расположении линии столбов под углом 45 градусов относительно наблюдателя – реальное расстояние будет:
809 * 0.7 = 566 метров (между 2-мя измеренными столбами). При больших углах – расст-е определяется по высоте опор.

Стандартное расстояние между опорами электросети высокого напряжения (ЛЭП) – 100 метров. Высота заводских труб – 30 м

Если нет линейки, то для измерений можно использовать подручные средства, например – спичечный коробок (5 сантиметров – максимум, 2.5см – до середины).

Точность определения дистанции по угловым величинам составляет 5-10% длины измеряемого расстояния.

Рис.6

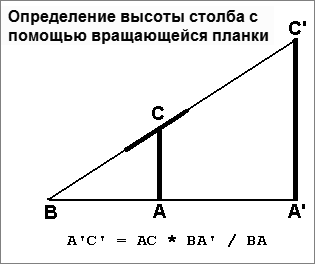
Определение высоты столба с помощью вращающейся планки

Нужно поставить на некотором расстоянии от столба А’С’ шест АС с вращающейся планкой и направить планку на верхнюю точку С’ столба (рис.7). С противоположной стороны, прицелившись по рейке – отметить на поверхности земли точку В.

Из подобия треугольников А’С’В и АСВ следует:
A’C’ = AC * BA’ / BA
то есть, чтобы определить высоту А’С’ столба, дастаточно будет знать высоту АС шеста и длину двух отрезков ВА’ и ВА

Можно померить и без дополнительных приспособлений. Один человек, лёжа на земле, смотрит на вершину объекта – по макушке головы стоящего помощника. Рост известен, горизонтальные расстояния – промеряются шагомерно. Данный способ применялся ещё во времена СССР, при проведении военно-патриотических и спортивных игр среди молодёжи (учащихся средних и старших классов общеобразовательных школ), с элементами военных учений, при участии кадровых офицеров вооруженных сил. У советских пионеров эти спортивно-массовые мероприятия назывались «Зарница», у старшеклассников – «Орлёнок». У зарубежных бой-скаутов, наверно, тоже могло быть что-то похожее.

Рис.7

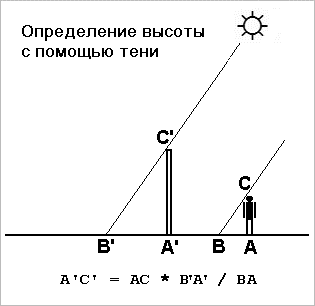
Определение высоты дерева с помощью тени

В солнечную погоду, измерить длину тени от дерева и от человека. Используя подобие треугольников, составить численную пропорцию (схема и формула показаны на рисунке 8) или построить графически, в выбранном масштабе.

В пасмурный день, когда не видно солнца на небе и лунной ночью, поставленная задача решается другими методами. Например, можно определить высоту с помощью способа, изображённого на рисунке 2 (построение прямоугольного равнобедренного треугольника), используя, дополнительно, современную лазерную указку, ориентированную по эккеру на 45° относительно земной поверхности – для визирования вершины предмета. Эккерная рамка ставится в вертикальной плоскости, а прямой угол между поверхностью земли и стороной квадрата крестовины — выставляется по отвесу.

Если произвольный угол A’B’C’ мерить при помощи угломера, тогда придётся смотреть в таблицах тангенсы угла и считать.

Рис.8

Определение высоты дерева с помощью зеркала

Если имеется зеркало, расположенное на земле горизонтально или лужа с дождевой водой, можно использовать оптическое свойство – равенство углов падения и зеркального отражения светового луча. Для этого, нужно встать на точке, из которой, в середине зеркала видна вершина предмета. Зная свой рост (на уровне глаз), расстояние до центра зеркала и от него до предмета, используя подобие треугольников, составить численную пропорцию (как на рисунке 8) или построить схему графически, в выбранном масштабе.

Определение крутизны скатов

С помощью отвеса (нить с небольшим грузиком) и транспортира (обычного измерителя или офицерской линейки). Становятся сбоку ската. Определяют, по шкале, угол между штрихом 90°, на транспортире, и вертикальной нитью.

Горизонтальным визированием и промером шагами, при крутизне подъёма до 20-25°. Располагаясь внизу ската, в точке А, визируют, горизонтально, на уровне глаз, выше по склону холма, точку В. Затем, парами шагов, промеряют расстояние АВ. Крутизна ската, при углах до 20-25°, определяется по формуле:

где А – крутизна ската, градусов; n – количество пар шагов. Точность определения – до 2-3°

Горизонтальным визированием, точным промером расстояния до намеченной точки (расположенной выше по склону горы), расчётом по формуле (катет треугольника – равен высоте до уровня глаз, гипотенуза – расстоянию) для синуса угла, и нахождением соответствующего числа по таблице.

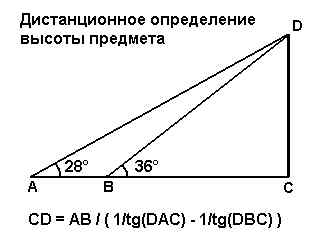
Дистанционное определение высоты предмета

Например, нужно определить высоту предмета (рис. 9), не подходя к нему (невозможно преодолеть препятствия в виде реки или глубокого оврага). Измеряются углы в точках А (DАС) и В (DВС), а так же расстояние АВ между ними. В примере на картинке:
DАС = 28°
DВС = 36°
АВ = 15 метров

тогда, высота предмета:
CD = АВ / ( 1/tg(DАС) – 1/tg(DВС) ) =
= 15 / ( 1/tg(28°) – 1/tg(36°) ) =
= 15 / ( 1/0.53 – 1/0.73 ) =
= 15 / ( 1.89 – 1.38 ) =
= 15 / 0.51 = 29 метров, с общей суммарной ошибкой измерений – до 10-20%

Рис.9

Примеры, разобранные на этой Интернет-странице, можно бесплатно скачать, сохранить на жёсткий диск своего компьютера или распечатать на принтере, чтобы удобнее было осваивать практические методы измерения расстояний и эффективнее тренироваться в реальных, полевых условиях. Правильное и точное определение ширины реки или водоёма – обязательно необходимо проводить перед форсированием водной преграды. В войсковых подразделениях, этим занимаются специалисты инженерной разведки.

Высокоточные измерения расстояний

При наличии дальномера (лазерные, свето- и радиодальномеры), получается довольно высокая точность, которая требуется при проведении геодезических работ, где эти приборы и применяют профессионалы. Туристам, в их походах и путешествиях, такие миллиметровые погрешности не нужны.

ПРИЛОЖЕНИЯ

Таблица синусов, косинусов, тангенсов и котангенсов углов от 0° до 90°
Точность вычислений – до третьего знака после запятой. Расчёт был проведён в электронных таблицах Excel по формулам, вида:
TAN(A1*pi()/180)
Пример: tg(60°) = 1.732

a	sin a	cos a	tg a	ctg a
0	0,000	1,000	0,000
1	0,017	1,000	0,017
2	0,035	0,999	0,035
3	0,052	0,999	0,052
4	0,070	0,998	0,070
5	0,087	0,996	0,087
6	0,105	0,995	0,105
7	0,122	0,993	0,123
8	0,139	0,990	0,141
9	0,156	0,988	0,158
10	0,174	0,985	0,176	5,671
11	0,191	0,982	0,194	5,145
12	0,208	0,978	0,213	4,705
13	0,225	0,974	0,231	4,331
14	0,242	0,970	0,249	4,011
15	0,259	0,966	0,268	3,732
16	0,276	0,961	0,287	3,487
17	0,292	0,956	0,306	3,271
18	0,309	0,951	0,325	3,078
19	0,326	0,946	0,344	2,904
20	0,342	0,940	0,364	2,747
21	0,358	0,934	0,384	2,605
22	0,375	0,927	0,404	2,475
23	0,391	0,921	0,424	2,356
24	0,407	0,914	0,445	2,246
25	0,423	0,906	0,466	2,145
26	0,438	0,899	0,488	2,050
27	0,454	0,891	0,510	1,963
28	0,469	0,883	0,532	1,881
29	0,485	0,875	0,554	1,804
30	0,500	0,866	0,577	1,732
31	0,515	0,857	0,601	1,664
32	0,530	0,848	0,625	1,600
33	0,545	0,839	0,649	1,540
34	0,559	0,829	0,675	1,483
35	0,574	0,819	0,700	1,428
36	0,588	0,809	0,727	1,376
37	0,602	0,799	0,754	1,327
38	0,616	0,788	0,781	1,280
39	0,629	0,777	0,810	1,235
40	0,643	0,766	0,839	1,192
41	0,656	0,755	0,869	1,150
42	0,669	0,743	0,900	1,111
43	0,682	0,731	0,933	1,072
44	0,695	0,719	0,966	1,036
45	0,707	0,707	1,000	1,000
46	0,719	0,695	1,036	0,966
47	0,731	0,682	1,072	0,933
48	0,743	0,669	1,111	0,900
49	0,755	0,656	1,150	0,869
50	0,766	0,643	1,192	0,839
51	0,777	0,629	1,235	0,810
52	0,788	0,616	1,280	0,781
53	0,799	0,602	1,327	0,754
54	0,809	0,588	1,376	0,727
55	0,819	0,574	1,428	0,700
56	0,829	0,559	1,483	0,675
57	0,839	0,545	1,540	0,649
58	0,848	0,530	1,600	0,625
59	0,857	0,515	1,664	0,601
60	0,866	0,500	1,732	0,577
61	0,875	0,485	1,804	0,554
62	0,883	0,469	1,881	0,532
63	0,891	0,454	1,963	0,510
64	0,899	0,438	2,050	0,488
65	0,906	0,423	2,145	0,466
66	0,914	0,407	2,246	0,445
67	0,921	0,391	2,356	0,424
68	0,927	0,375	2,475	0,404
69	0,934	0,358	2,605	0,384
70	0,940	0,342	2,747	0,364
71	0,946	0,326	2,904	0,344
72	0,951	0,309	3,078	0,325
73	0,956	0,292	3,271	0,306
74	0,961	0,276	3,487	0,287
75	0,966	0,259	3,732	0,268
76	0,970	0,242	4,011	0,249
77	0,974	0,225	4,331	0,231
78	0,978	0,208	4,705	0,213
79	0,982	0,191	5,145	0,194
80	0,985	0,174	5,671	0,176
81	0,988	0,156	0,158
82	0,990	0,139	0,141
83	0,993	0,122	0,123
84	0,995	0,105	0,105
85	0,996	0,087	0,087
86	0,998	0,070	0,070
87	0,999	0,052	0,052
88	0,999	0,035	0,035
89	1,000	0,017	0,017
90	1,000	0,000	0,000

При отсутствии таблиц Брадиса, инженерного калькулятора и компьютера, значения тригонометрических функций можно посчитать, с произвольно высокой точностью, и на простейшем арифмометре, с помощью арифметических операций сложения, вычитания, умножения и деления по формулам рядов:

sin x = x – x^3/1*2*3 + x^5/1*2*3*4*5 – x^7/1*2*3*4*5*6*7 + x^9/1*2*3*4*5*6*7*8*9 -.

cos x = 1 – x^2/1*2 + x^4/1*2*3*4 – x^6/1*2*3*4*5*6 + x^8/1*2*3*4*5*6*7*8 -.

tg x = x + (1/3 * x^3) + (2/15 * x^5) + (17/315 * x^7) + .

В степень – число возводится с помощью многократного перемножения.
Например, аргумент в кубе: x^3 = x*x*x На калькуляторе, после набора числа, последовательно нажимаются кнопки: * = =

Главные формулы из геометрии, использовавшиеся в разобранных примерах

Теорема Пифагора: a^2 + b^2 = c^2

В прямоугольном треугольнике ABC (рис.10) – отношение двух его сторон, например катета a к гиптенузе c, зависит от величины одного из острых углов, например A.

Основные тригонометрические функции для прямоугольного треугольника:

Синус: sin A = a / c (отношение противолежащего катета к гипотенузе)
Косинус: cos A = b / c
Тангенс: tg A = a / b
Котангенс: ctg A = b / a

A + B = 90°
B = 90° – A

a = c * sin A = c * cos B
a = b * tg A

Рис.10 Основные тригонометрические формулы для прямоугольного треугольника.

Если на карте отсутствует масштабная линейка и не указан численный масштаб

На топокарте, по вертикали (на линии север-юг) в 1 минуте, приблизительно – 1.85 километров (мало зависимо от географической широты на земном глобусе). И если имеется подписанная градусная сетка, то по ней, графически, турист может определить, сколько в одном сантиметре, для измерения расстояний в любых направлениях на карте. Когда указаны не минуты, а доли градуса, то соотношение:

0.1 градуса = 11.1 км
0.01 градуса = 1.11 км

// Международная морская миля (действует с 1929 года), применяемая в географии и в навигации, для определения расстояний, равна 1852 метра, что, примерно, соответствует одной минуте дуги земного меридиана на сороковых широтах. Это удобно для навигационных расчетов, при решении прикладных задач. В судоходстве, в качестве основной единицы скорости движения, применяется УЗЕЛ (от англ. knot «узел»; 1 kn равен 1 пройденной морской миле, за час движения). Международный КАБЕЛЬТОВ (единица длины, для измерения, в мореходной практике, сравнительно небольших расстояний, равен 1/10 морской мили.

Список использованной литературы и ссылки на Интернет-ресурсы

Андреев Н.В. Топография и картография: Факультативный курс. М., Просвещение, 1985

https:// school-kraevedenie.narod.ru/ antimonov/ – Школьные походы по изучению рек, озер и болот родного края. Москва, 1963 г.

Краткий справочник. Издание военно-инженерной Академии Красной Армии имени В.В.Куйбышева, 1941 год.

www.festival.1september.ru/ articles/418615/ – Измерительные работы на местности в курсе геометрии основной школы.

www.kakras.ru/mobile/tourism-compass-and-map.html – Карта и компас (дирекционный угол, движение по азимутам и примеры расчётов).

Контроль выбросов в атмосферу на сайте ООО «Лабораторно-исследовательский Центр».

Окружность можно нарисовать на листе бумаги – с помощью нитки и воткнутой булавки. Туристические минисправочники. Прикладная топография.

Источник