Определение соответствия способы задания соответствий

Тема 3. Понятие соответствия Содержание

Понятие соответствия между множествами.

Способы задания соответствий.

Соответствие обратное данному.

Взаимно однозначное соответствие.

Равномощные множества. Счетные множества.

Основная литература 7, 10, 11, 16, 23, 33, 34;

Дополнительная литература 1, 10, 14, 74

1. Понятие соответствия между множествами

В начальном курсе математики изучаются различные взаимосвязи между элементами одного, двух и более множеств. Поэтому учителю надо понимать их суть, что поможет ему обеспечить единство в методике этих взаимосвязей.

Рассмотрим примеры соответствий, изучаемых в начальном курсе математики.

Пример 1. а) (17 – 1) : 4; б) (12 + 18) : (6-6); в) 27 + 6. Пример 2. 1) 2+х =6; 2) х-7=4; 3) 2х=8.

В первом примере мы установили соответствие между заданными выражениями и их числовыми значениями. Во втором выяснили, какое число является решением уравнения.

Все эти соответствия имеют общее – во обоих случаях мы имеем два множества: в первом – это множество из трех числовых выражений и множество N натуральных чисел (ему принадлежат значения данных выражений); во втором – это множество из трех уравнений и множество N натуральных чисел.

Связь (соответствие) между этими множества можно представить наглядно, при помощи графов.

N 1 N 2

Полученные множества показывают, что любое соответствие между двумя множествами Х и У можно рассматривать как множество упорядоченных пар, образованных из их элементов. А так как упорядоченные пары – это элементы декартова произведения, то приходим к следующему определению общего понятия соответствия.

Определение. Соответствием между множествами Х и У называется всякое подмножество декартова произведения этих множеств. Соответствия принято обозначать буквами R, P, F, T и др.

2. Способы задания соответствий

Поскольку соответствие – это подмножество, то его можно задать как любое множество, т.е. либо перечислив все пары элементов, находящихся в заданном соответствии, либо указав характеристическое свойство элементов этого подмножества.

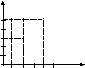
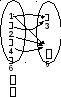
Пример. Соответствие между множествами Х = 1, 2, 4, 6 и У = 3, 5 можно задать: 1) при помощи предложения с двумя переменными: а  в при условии, что а  Х, в  У; 2) перечислив пары чисел, принадлежащих подмножеству декартова произведения ХУ: (1,3),(1,5),(2,3),(2,5),(4,5). К этому способу задания относят также задание соответствия при помощи графа и графика.

у

Х У

3. Соответствие обратное данному

Пример. Пусть S – соответствие «больше на 2» между множествами Х = 4, 5, 8, 10 и У = 2, 3, 6. Тогда S = (4,2), (5,3), (8,6) и его граф будет как на рисунке.

С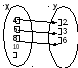оответствие обратное данному, — это соответствие «меньше на 2». Оно рассматривается между множествами У и Х, и чтобы его представить наглядно, достаточно на графе соответствия S направление стрелок поменять на противоположное (См. рисунок).

Условимся предложение «элемент х находится в соответствии S с элементом у» записывать кратко так: х S у.

Определение. Пусть S – соответствие между множествами Х и У. Соответствие S -1 между множествами У и Х называется обратным данному, если у S -1 х тогда и только тогда, когда х S у. Соответствия S и S -1 называют взаимно обратными.

Выясним особенности их графиков. Построим график соответствия S = (4,2), (5,3), (8,6)

у

у

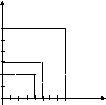
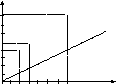
При построении графика соответствия S -1 = (2,4), (3,5), (6,8) мы должны первую компоненту выбирать из множества У = 2,3,6, а вторую – из множества Х = 4, 5, 8, 10. В результате график соответствия S -1 совпадет с графиком соответствия S. Чтобы различать графики соответствий S и S -1 , условились первую компоненту пары соответствия S -1 считать абсциссой, а вторую – ординатой. Например, если (5,3)  S, то (3,5)  S -1 . Точки с координатами (5,3) и (3,5), а в общем случае (х,у) и (у,х) симметричны относительно биссектрисы 1-го и 3-го координатных углов. Следовательно, графики взаимно обратных соответствий S и S -1 симметричны относительно биссектрисы 1-го и 3-го координатных углов.

Чтобы построить график соответствия S -1 , достаточно изобразить на координатной плоскости точки, симметричные точкам графика S относительно биссектрисы 1-го и 3-го координатных углов.

Источник

Понятие соответствия между элементами двух множеств. Способы задания соответствий. Соответствие обратное данному. Взаимно однозначные соответствия. Равномощные множества

Соответствие между элементами мн-в А и В называют любое под множ-во их декартово произведения.

Способы задания соответствия

1 – указаниям характеристик св-ва по кот. Эти пары составл.

2- перечисление этих пар.

Пример: если мн-ва

3)С помощью графа.

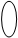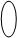4)С помощью таблицы

X/Y
(1,1)	(1,3)	(1,5)	(1,7)
(2,1)	(2,3)	(2,5)	(2,7)
(3,1)	(3,3)	(3,5)	(3,7)

Определение:

Между элементами назыв обратно данному если yS (В минус 1 степени) xó xSy

S(В минус первой степени) входит B x А.

Чтобы постр графического обратного соответствия надо поменять направления стрелок.

Чтобы задать соответствие обратное данному в перечисление пар надо поменять местами компоненты пар. Графики взаимно обратных соответствий семетричны. Относительно прямой координатных углов.

Определение:

Взаимно однозначном соответствием между элементам мн-в А и В назыв. такое соответствие при которым каждому элементу. Из мн-в А соответствует единст элемент.

Из мн-ва В и каждый элемент из мн-ва В является соответсвующим только для одного элемента из мн-ва А.

Пример: Мн-во первых 24 натур чисел, мн-во студен в группе.

Мн-во А и В назыв равномощным если между их элементами можно установить взаимно однозначно А

2. Обучающимся начальных классов предложено задание:

1 2 3 4 5 6 7 8

• При изучении какой темы курса математики начальных классов можно предложить это задание?

• С какой целью и на каком этапе?

• Соответствие между какими множествами здесь задается? Являются ли эти множества равномощными?

• Опишите методику введения знаков ”>“ и “

Источник

Презентация по ТОНКМ с методикой обучения на тему «Отношения и соответствия»

Описание презентации по отдельным слайдам:

Отношения и соответствия План: Отношения между элементами одного множества. Понятие отношения, способы задания. Свойства отношений. Отношение эквивалентности и порядка. Соответствие между элементами двух множеств. Понятие соответствия, способы задания. Взаимно однозначные соответствия. Задания для самостоятельной работы. Вопросы для самоконтроля.

В математике рассматривают связи между элементами одного множества и называют их отношениями. Если рассматривают отношения между двумя элементами, то их называют бинарными. Отношения многообразны: между понятиями – это отношения род и вида, части и целого; между предложениями – это отношения следования и равносильности; между числами – «больше», «меньше», «равно», «больше на…» и т. п.

Рассмотрим на множестве отрезков на рис.1 отношения перпендикулярности равенства «длиннее» Рисунок1 Построим графы данных отношений. Сравним их и выделим свойства.

Рисунок 2 «Граф отношений равенства»

Рисунок 3 «Граф отношения перпендикулярности»

Рисунок 4 «Граф отношения длиннее»

Определение. Отношение R на множестве Х называется рефлексивным, если о каждом элементе множества Х можно сказать, что он находится в отношении R с самим собой. На графе: «петля» в каждой вершине графа. Рефлексивны отношения: равенства (рисунок 2 «каждый отрезок равен сам себе»). кратности (каждое N число кратно самому себе). подобия.

На графе: две вершины соединены только одной стрелкой. Существуют отношения, которые не обладают ни свойством симметричности, ни свойством антисимметричности. Пример. Дано отношение «быть сестрой» на множестве детей одной семьи: Катя, Маша, Толя. К М Т

Если на множестве Х задано отношение эквивалентности, то оно порождает разбиение этого множества на попарно непересекающиеся подмножества (классы эквивалентности). Верно и обратное утверждение. Определение. Отношение R на множестве Х называется отношением порядка, если оно транзитивно и антисимметрично. Является отношением порядка отношения: «меньше» «длиннее»

Данное соответствие взаимно однозначное, т.к. каждому соответствует единственный

Курс повышения квалификации

Охрана труда

• Сейчас обучается 93 человека из 44 регионов

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

• Сейчас обучается 336 человек из 66 регионов

Курс профессиональной переподготовки

Охрана труда

• Сейчас обучается 171 человек из 48 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-092237

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Правительство предложило потратить до 1 млрд рублей на установку флагов РФ у школ

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

В России выбрали топ-10 вузов по работе со СМИ и контентом

Время чтения: 3 минуты

В Москве запустили онлайн-проект по борьбе со школьным буллингом

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Понятие соответствия. Способы задания соответствий

Рассмотрим три примера соответствий, изучаемых в начальном курсе математики.

I. Найти значение выражения:	II. Найти площадь фигуры:	III. Решить уравнение:
в1) (17 – 1) : 4	F1	y1) 2+x = 6
в2) (12 + 18) : (6-6);	F2	y2) x – 7 = 4
в3) 2×7+6	F3 Рис.66	y3) 2x = 8

В первом случае мы устанавливаем соответствие между заданными выражениями и их числовыми значениями. Во втором выясняем, какое число соответствует каждой из данных фигур, характеризуя ее площадь. В третьем ищем число, которое является решением уравнения.

Что общее имеют эти соответствия?

Видим, что во всех случаях мы имеем два множества: в первом — это множество из трех числовых выражений и множество N натуральных чисел (ему принадлежат значения данных выражений); во втором — это множество из трех геометрических фигур и множество N натуральных чисел; в третьем — это множество из трех уравнений и множество N натуральных чисел.

Выполняя предложенные задания, мы устанавливаем связь (соответствие) между этими множествами. Ее можно представить наглядно, при помощи графов (рис. 67).

Можно задать эти соответствия, перечислив все пары элементов, находящихся в заданном соответствии:

Полученные множества показывают, что любое соответствие между двумя множествами X и Y можно рассматривать как множество упорядоченных пар, образованных из их элементов. А так как упорядоченные пары — это элементы декартова произведения, то приходим к следующему определению общего понятия соответствия.

Определение.Соответствием между множествами X и Y назы­вается всякое подмножество декартова произведения этих множеств.

Соответствия принято обозначать буквами Р, S, Т, R и др. Если S-соответствие между элементами множеств X и Y, то, согласно определению, S ÌХ ´ Y.

Выясним теперь, как задают соответствия между двумя множествами. Поскольку соответствие — это подмножество, то его можно задавать как любое множество,т.е. либоперечислив все пары элементов, находящихся в заданном соответствии, либоуказав характеристическое свойство элементов этого подмножества. Так, соответствие между множествами X = <1, 2, 4, 6>и Y = <3, 5>можно задать:

3)при помощи предложения с двумя переменными: а -1 , то S -1 = <(2,4), (3,5), (6,8)>.

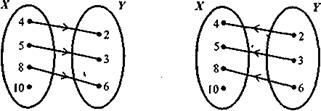а) б)

Рис. 70

Условимся предложение «элемент х находится в соответствии S с элементом у» записывать кратко так: хSу. Запись хSу можно рассматривать как обобщение записей конкретных соответствий: х = 2у; х > 3у+1 и др.

Воспользуемся введенной записью для определения понятия соответствия, обратного данному.

Определение. Пусть S — соответствие между множествами Х иY. Соответствие S -1 между множествами Y и X называется обратным данному, если у S -1 х тогда и только тогда, когда хSу.

Соответствия S и S называют взаимно обратными. Выясним особенности их графиков.

Построим график соответствия S = <(4, 2), (5, 3), (8, 6)>(рис. 71, а). При построении графика соответствия S -1 = <(2, 4), (3, 5), (6, 8)>мы должны первую компоненту выбирать из множества Y = <2, 3, 6>, а вторую — из множества Х= <4, 5, 8, 10>. В результате график соответствия S -1 совпадет с графиком соответствия S. Чтобы различать графики соответствий S и S -1 , условились первую компоненту пары соответствия S -1 считать абсциссой, а вторую — ординатой. Например, если (5, 3) Î S, то (3, 5) Î S -1 . Точки с координатами (5, 3) и (3, 5), а в общем случае (х, у) и (у, х) симметричны относительно биссектрисы 1-го и 3-го координатных углов. Следовательно, графики взаимно обратных соответствий S и S -1 симметричны относительно биссектрисы 1-го и 3-го координатных углов.

Чтобы построить график соответствия S -1 , достаточно изобразить на координатной плоскости точки, симметричные точкам графика S относительно биссектрисы 1-го и 3-го координатных углов.

Упражнения

5. Вычислив длины заданных отрезков, учащийся записал: АВ — 7 см, СD = 12 см, КL = 15 см, ХY — 12 см. Соответствие между какими множествами он установил? Задайте это соответствие при помощи предложения с двумя переменными и графа.

6.Даны множества: X — <2, 5), Y = <3, 6>. Перечислите элементы декартова произведения данных множеств и образуйте все подмножества полученного множества. Какое из подмножеств задает соответствие: а) «больше»; б) «меньше»; в) «меньше на 1»; г) «меньше в 3 раза»?

3. Соответствие «число х в два раза больше числа у» рассматривается между множествами X и Y. Каким будет его график, если:

4. Между множествами X = <0, 1, 2, 3, 4, 5>и Y = Z задано соответствие «х — у = 3», причем х е X, у е Y. Какая фигура на рисунке 72 является графиком этого соответствия?

10. Графиком соответствия Р, заданного между множествами X и Y, являются все точки прямоугольника АВСБ (рис. 73). Назовите координаты трех точек, принадлежащих этому графику и задайте множества Х и Y.

11. Множества X = <1, 3, 4, 6>и Y = <0, 1>находятся в соответствии S = <(1, 1), (3, 0), (3, 1), (4, 0), (4, 1) (6, 1)>. Задайте соответствиеS -1 , обратное соответствию Y, и постройте на одном чертеже их графики.

12. Между множеством X — углов треугольника AВС и множеством Y — его сторон задано соответствие Т — «угол х лежит против стороны у». Задайте соответствие Т -1 , обратное соответствию Т, при помощи: а) предложения с двумя переменными; б) графа.

13. Даны графики соответствий Р и Q (рис. 74). Можно ли утверждать, что соответствия Р и Q взаимно обратные?

14.Постройте графики соответствий, обратных данным (рис. 75).

Не нашли, что искали? Воспользуйтесь поиском:

Источник