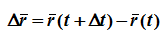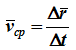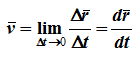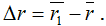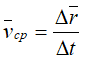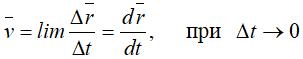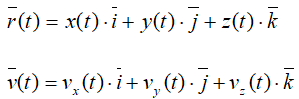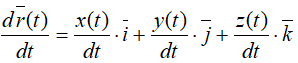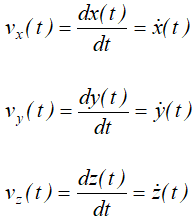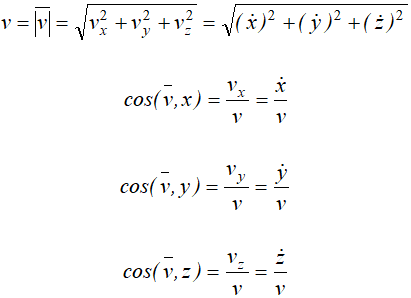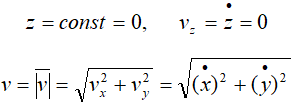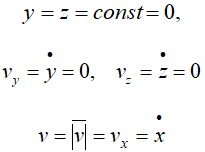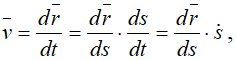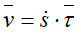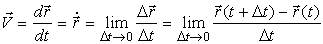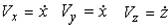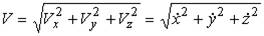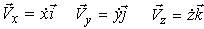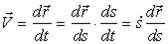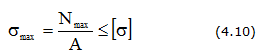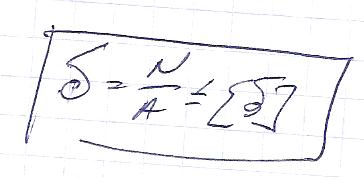- iSopromat.ru
- Скорость точки при векторном способе задания движения
- Скорость точки при координатном способе задания движения
- Скорость точки при естественном способе задания движения
- Скорость точки при различных способах задания движения.
- Скорость точки и ее определение при различных способах задания движения.
iSopromat.ru
Скоростью точки называют кинематическую меру ее движения, равную производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета.
Скорость относительно выбранной системы отсчета это одна из основных характеристик движения точки.
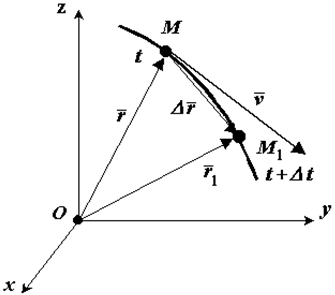
Вектор скорости направлен по касательной к траектории точки в сторону движения.
Рассмотрим перемещение точки за малый промежуток времени Δ t:
средняя скорость точки за промежуток времени D t.
Наш видеоурок по теме:
Скорость точки в данный момент времени
Скорость точки при векторном способе задания движения
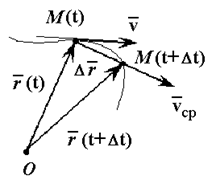
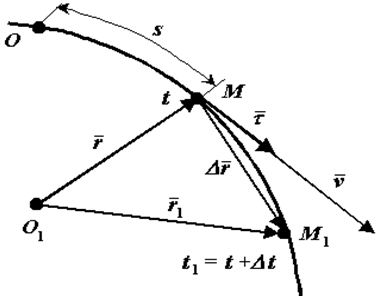
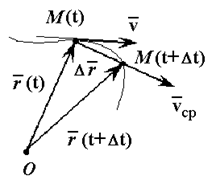
Положение движущейся точки М относительно системы отсчета в момент времени t1 определяется радиус-вектором r.
В другой момент времени t1=t+Δt точка займет положение М1 с радиус-вектором r1.
За время Δt радиус-вектор движущейся точки изменится на
Средней скоростью vср называется отношение изменения радиус-вектора Δr к изменению времени Δt.
Скорость точки равна первой производной по времени от ее радиус-вектора.
Скорость точки при координатном способе задания движения
Разложим радиус-вектор и скорость на составляющие, параллельные осям координат. Получим
Проекция скорости точки на какую-либо координатную ось равна первой производной по времени от соответствующей координаты этой точки.
Модуль скорости и направляющие косинусы равны:
Если точка движется в плоскости, то, выбрав оси координат Ox и Oy в этой плоскости, получим:
Для прямолинейного движения точки координатную ось, например ось Ox, направляем по траектории. Тогда
Скорость точки при естественном способе задания движения
Пусть скорость точки задана естественным способом, т.е. заданы траектория точки и закон ее движения по траектории s=f(t).
Вычислим скорость точки. Используем радиус-вектор r. движущейся точки, начало которого находится в неподвижной точке O1
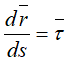
— единичный вектор, направленный по касательной к траектории в сторону возрастающих расстояний.
При ds>0 направления векторов τ и dr совпадают.
Если точка движется в сторону убывающих расстояний, то ds
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник
Скорость точки при различных способах задания движения.
Положение точки определяется пространственными параметрами: радиус-вектором, декартовыми координатами, дуговой координатой и др. Скорость точки является пространственно — временным параметром.
Скоростью точки называется кинематический параметр, характеризующий быстроту изменения положения точки в системе отсчета с течением времени.
Скорость точки при векторном способе задания движения.
Пусть движение точки относительно тела отсчета задано ее радиус-вектором r(t). Тогда, по определению, скоростью точки будет векторная производная радиус-вектора r по скалярному аргументу — времени t:
Пусть движение точки задано в декартовой системе координат Oxyz, которую считаем неподвижной, и известны кинематические уравнения движения точки: x = x(t); y = y(t); z = z(t). Используя равенство (5) в п. 26, по формуле (1) выражаем скорость точки:
Так как система координат Oxyz неподвижна, ее единичные векторы i,j,k постоянны (не меняют ни величину, ни направление), то слагаемые, содержащие производные этих векторов, равны нулю и
Проекциями вектора скорости на оси координат являются сомножители перед единичными векторами, следовательно,
Зная проекции скорости на оси координат, можно определить величину вектора скорости:
Направление вектора скорости определяется тремя направляющими косинусами: (11)
Формула (9) позволяет не только определить скорость аналитически, но и построить вектор скорости геометрически. По этой формуле вектор скорости можно представить как сумму трех взаимно перпендикулярных составляющих: (12)
Геометрически сложив составляющие, найдем вектор скорости. При построении составляющих по формулам (21) нужно учитывать: 1) если производная координаты положительна, то направление составляющей совпадает с направлением единичного вектора координатной оси; 2) если производная отрицательна, составляющая направлена в противоположную сторону.
Нахождение скорости при естественном способе задания движения.
При движении точки по траектории радиус-вектор будет меняться с изменением дуговой координаты, а сама дуговая координата является функцией времени, то есть радиус-вектор является сложной функцией времени r = r (s(t)). По формуле (1) выразим вектор скорости точки: (14)
Рассмотрим вектор dr / ds. Согласно формуле (14), этот вектор направлен по касательной к траектории, так как скорость направлена по касательной, а так как при Δs 0 предел отношения длины дуги |Δs| к длине ее хорды MM1 = Δr (рис. 61) равен единице, то по модулю он равен единице. Следовательно, (15)
где является единичным вектором касательной к траектории в точке M.
Вектор всегда направлен в сторону возрастания дуговой координаты. На рис. 61 показан случай, когда Δs > 0 (дуговая координата точки больше координаты точки M1). Сам вектор Δ/Δs направлен в сторону вектора Δ, в сторону положительного отсчета дуги. Когда Δs 0, вектор скорости направлен по вектору , когда
Если плоскость действия изгибающего момента в сечении не совпадает ни с одной из главных осей сечения, изгиб называют косым.
Далее будет показано, что при плоском изгибе ось балки и после деформации остается в плоскости внешних сил — силовой плоскости. При косом изгибе плоскость деформации не совпадает с силовой плоскостью
Источник
Скорость точки и ее определение при различных способах задания движения.
Рассмотрим перемещение точки за малый промежуток времени Δt:
средняя скорость точки за промежуток времени Dt . Скорость точки в данный момент времени
Скорость точки – это кинематическая мера ее движения, равная производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета. Вектор скорости направлен по касательной к траектории точки в сторону движения.
· Ускорение точки— векторная величина, характеризующая быстроту изменения скорости по величине и направлению, м\с^2
Ускорения раскладывают на две составляющие:
· Касательное(тангенциальное)- характерезует изменение скорости по величине и всегда направленно по касательной к траектории. At=v
· Нормальное ускорение— характеризует изменение скорости по направлению( центростремительной). Нормальное ускорение направленно перпендикулярно скорости в центре кривизны траектории. An=V^2\R.
34. Поступательное движение твердого тела. Кинематические параметры, характеризующие поступательное движение
При поступательном движении тела все точки тела движутся одинаково, и, вместо того чтобы рассматривать движение каждой точки тела, можно рассматривать движение только одной его точки.
Основные характеристики движения материальной точки:
· перемещение точки, пройденный ею путь, координаты,
Линию, по которой движется материальная точка в пространстве, называют траекторией.
Перемещением материальной точки за некоторый промежуток времени называется вектор перемещения ∆r=r-r0, направленный от положения точки в начальный момент времени к ее положению в конечный момент.
Скорость материальной точки представляет собой вектор, характеризующий направление и быстроту перемещения материальной точки относительно тела отсчета.
Вектор ускорения характеризует быстроту и направление изменения скорости материальной точки относительно тела отсчета.
37.Равномерное вращательное движение тела. Уравнение равномерного вращения. Кинематические графики.
1.Во время равномерного вращательного движения тело совершает движение по окружности с одинаковой скоростью, но с изменяющимся направлением. Например, такое движение совершают стрелки часов по циферблату.
Допустим, шар равномерно вращается на нити длиной 1 метр. При этом он будет описывать окружность с радиусом 1 метр. Длина такой окружности: C = 2πR = 6,28 м
Время, за которое шар полностью делает один полный оборот по окружности, называется периодом вращения — T.
Чтобы вычислить линейную скорость шара, необходимо разделить перемещение на время, т.е. длину окружности на период вращения:
Если наш шар будет делать один оборот за 1 секунду (период вращения = 1с), то его линейная скорость:
V = 6,28/1 = 6,28 м/с
2.Если угловая скорость ω=const, то вращательное движение называется равномерным.
Уравнение равномерного вращения имеет вид
В частном случае, когда начальный угол поворота φ0=0,
Угловую скорость равномерно вращающегося тела
можно выразить и так:
где T – период вращения тела; φ=2π – угол поворота за один период.
38.Равнопеременное вращательное движение тела. Уравнение равнопеременного вращение. Кинематические графики.
Если угловое ускорение ε=const, то вращательное движение называется равнопеременным. Таким образом, равнопеременное вращение тела – частный случай неравномерного вращательного движения.
Уравнение равнопеременного вращения: φ = φ0 + ω0t + εt2/2
и уравнение, выражающее угловую скорость тела в любой момент времени,
представляют совокупность основных формул вращательного равнопеременного движения тела.
В эти формулы входят всего шесть величин: три постоянных для данной задачи φ0, ω0 и ε и три переменных φ, ω и t. Следовательно, в условии каждой задачи на равнопеременное вращение должно содержаться не менее четырех заданных величин
Угловое ускорение при ускоренном движении — величина положительная; угловая скорость будет все время возрастать.
Угловое ускорение при замедленном движении— величина отрицательная; угловая скорость убывает.
Для данного движения кинематические графики представлены на рис. 11.5.
39.Основные понятия и аксиомы динамики.
· Динамика-раздел теоретической механики, в котором устанавливается связь между движением тел и действующими на них силами.
В динамике различают два типа задач:
—определяют параметры движения по заданным силам
— определяют силы, действующие на тело, по заданным кинематическим параметрам движения.
· Масса— кол-во в-ва в объеме тела, в классической механике ее считают величиной постоянной, кг.
1. (Принцип инерции)
Всякая изолированная материальная точка находится в состоянии покоя или равномерного и прямолинейного движения, пока приложенные силы не выведут ее из этого состояния.
2. (второй закон Ньютона- основной закон динамики)
Зависимость между силой, действующей на материальную точку, и сообщаемым его ускорением следующая: F=ma,
Где m- масса точки, кг; a- ускорение точки, м\с^2.
Ускорение, сообщенное материальной точке силой, пропорционально величине силы и совпадает с направлением силы.
Основ. закон динамики в дифф. форме:
На все тела на Земле действует сила тяжести, она сообщает телу ускорение свободного падения, направленное к центру Земли: G=mg, где g=9,81 м\с^2-ускорение свободного падения.
3. (третий закон Ньютона)
Силы взаимодействия двух тел равны по величине и направленны по одной прямой в разные стороны:
F1=F2, F1=m1a1, F2=m2a2, откуда m1a1=m2a2 или m1\m2=a2\a1
При взаимодействии ускорение обратно пропорциональным массам.
4. (закон независимости действия сил)
Каждая сила системы сил действует так, как она действовала бы одна.
Ускорение, сообщаемое точке системой сил, равно геометрической сумме ускорений, сообщенных точке каждой силой в отдельности:
40. Сила инерции
Инертность — способность сохранять свое состояние неизменным, это внутреннее свойство всех материальных тел.
Сила инерции — сила, возникающая при разгоне или торможении тела (материальной точки) и направленная в обратную сторону от ускорения. Силу инерции можно измерить, она приложена к «связям» — телам, связанным с разгоняющимся или тормозящимся телом.
41. Работа постоянной силы на прямолинейном пути.
Работа силы в общем случае численно равна произведению модуля силы на длину пройденного пути и на косинус угла между направлением силы и направлением перемещения.
Ед. измерения работы: 1Дж= 1Н*м; 1кДж= 10^3 Дж
42. Работа силы тяжести. –зависит только от изменения высоты и равна произведению модуля силы тяжести на вертикальное перемещение точки:
43. Работа равнодействующей силы.
Под действием системы сил точка массой m перемещается из положения M1 в положение М2.
В случае движения под действием системы сил получаются теоремой о работе равнодействующей.
Работа равнодействующей на некотором перемещении равна алгебраической сумме работ системы сил на том же перемещении.
44. Мощность при поступательном движении. Единицы измерения мощности.
Для характеристики работоспособности и быстроты совершения работы введено понятие мощности.
Мощность — работа, выполненная в единицу времени: P=W/t
Единица измерения мощности: ватты, киловатты
Мощность при поступательном движении:
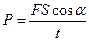

где F — модуль силы, действующей на тело; vcp — средняя скорость движения тела.
Средняя мощность при поступательном движении равна произведению модуля силы на среднюю скорость перемещения и на косинус угла между направлениями силы и скорости.
Каждая машина и механизм, совершая работу, тратит часть энергии на преодоление вредных сопротивлений.
46. Трение. Виды трения.
Трение- процесс взаимодействия тел при их относительном движении( смещении) либо при движении тела в газообразной или жидкой среде.
· Трение скольжения- сила, возникающая при поступательном перемещении одного из контактирующих\взаимодействующих тел относительно другого и действующая на это тело в направлении, противоположном направлению скольжения.
· Трение качения- момент сил, возникающий при качении одного из двух контактирующих\взаимодействующих тел относительно другого.
· Трение покоя- сила, возникающая между двумя контактирующими телами и препятствующая возникновению относительно движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Возникает при микроперемещениях ( например, при деформации) контактирующих тел. Она действует в направлении, противоположном направлению возможного относительного движения.
47. Сила трения скольжения — силы, возникающие между соприкасающимися телами при их относительном движении. Если между телами отсутствует жидкая или газообразная прослойка (смазка), то такое трение называется сухим. В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя.
· Первый закон. Сила трения скольжения равна сдвигающей силе и заключена между нулем и максимальным значением, которое достигается в момент выхода тела из положения равновесия
· Второй закон. Максимальная сила трения скольжения при всех прочих условиях не зависит от площади соприкосновения трущихся поверхностей.
Из этого закона следует, что для того, чтобы сдвинуть, например, кирпич, надо приложить одну и ту же силу независимо от того, какой гранью он положен на поверхность – широкой или узкой.
· Третий закон. Максимальная сила трения скольжения пропорциональна силе нормального давления тела на опорную поверхность
(условие начала скольжения тела).




· Четвертый закон. Коэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей (степени шероховатости, влажности, температуры и других условий).
48. Сопротивление материалов— раздел технической механики, в котором излагаются теоретико-экспериментальные основы и методы расчета наиболее распространенных элементов конструкций на прочность, жесткость и устойчивость.
Упругая деформация – это деформация, которая исчезает после снятия нагрузки. Упругая деформация не вызывает остаточных изменений в свойствах и структуре металла; под действием приложенной нагрузки происходит незначительное обратимое смещение атомов.
Пластической называется деформация, остающаяся после прекращения действия вызвавших ее напряжений. При пластической деформации в кристаллической решетке металла под действием касательных напряжений происходит необратимое перемещение атомов. При небольших напряжениях атомы смещаются незначительно и после снятия напряжений возвращаются в исходное положение. При увеличении касательного напряжения наблюдается необратимое смещение атомов на параметр решетки, т. е. происходит пластическая деформация.
49. Сопротивление материалов— раздел технической механики, в котором излагаются теоретико-экспериментальные основы и методы расчета наиболее распространенных элементов конструкций на прочность, жесткость и устойчивость.
Допущения о св-ах материалов: Материалы однородные— в любой точке материалы имеют одинаковые физико- механические св-ва.
Материалы представляют сплошную среду– кристаллическое строение и микроскопические дефекты не учитываются.
Материалы изотропны— механические св-ва не зависят от направления нагружения.
Материалы обладают идеальной упругостью- полностью восстанавливают форму и размеры после снятия нагрузки.
Допущения о характере деформации: Все материалы под нагрузкой деформируются, т.е. меняют форму и размеры.
50.Основные требования к деталям и конструкциям.
Виды расчетов в сопротивлении материалов (есть)
Механические свойства материалов
1. Прочность — способность не разрушаться под нагрузкой. Жесткость — способность незначительно деформироваться под нагрузкой.
2. Выносливость— способность длительное время выдерживать временные нагрузки.
3. Устойчивость — способность сохранять первоначальную форму упругого равновесия.
4. Вязкость — способность воспринимать ударные нагрузки.
ü Расчет на прочность обеспечивает неразрушение конструкции.
ü Расчет на жесткость обеспечивает деформации конструкции год нагрузкой в пределах допустимых норм.
ü Расчет на выносливость обеспечивает необходимую долговечность элементов конструкции.
ü Расчет на устойчивость обеспечивает сохранение необходимой формы равновесия и предотвращает внезапное искривление длинных стержней.
ü Для обеспечения прочности конструкций, работающих при ударных нагрузках (при ковке, штамповке и подобных случаях), проводятся расчеты на удар.
51. Классификация нагрузок и элементов конструкции.



52. Метод сечений. Внутренние силовые факторы.
Для проведения расчетов на прочность и жесткость необходимо установить зависимость между внешними и внутренними силами, действующими на элементы конструкции и возникающими при этом внутренними силами. Для этого используют метод сечений, который сводится к следующему:
1. Разрезают тело плоскости в том месте, где нужно определить внутренние силы.
2. Отбрасывают любую часть тела.
3. Действие отброшенной части заменяют внутренними силами, что бы оставшаяся часть находилась в равновесии.
4. Составляет условие равновесия для рассматриваемой части.
53. Метод сечений. Напряжения: полное, нормальное, касательное.
Для проведения расчетов на прочность и жесткость необходимо установить зависимость между внешними и внутренними силами, действующими на элементы конструкции и возникающими при этом внутренними силами. Для этого используют метод сечений, который сводится к следующему:
1. Разрезают тело плоскости в том месте, где нужно определить внутренние силы.
2. Отбрасывают любую часть тела.
3. Действие отброшенной части заменяют внутренними силами, что бы оставшаяся часть находилась в равновесии.
4. Составляет условие равновесия для рассматриваемой части.
· Напряжение- внутренняя сила, приходящаяся на ед. площади сечения.
· Сигма- нормальное напряжение, характеризует сопротивление сечение растяжению или сжатию.
· Таз- касательное напряжение, характеризует сопротивление сечения сдвигу.
54. Растяжение и сжатие.
-Пик деформации, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор- Продольная сила.
Продольная сила- составляющая внутренних сил, действующая перпендикулярно к плоскости поперечного сечения тела. Продольные силы меняются по длине бруса.
55.Напряжения при растяжении и сжатии.
Растяжением или сжатием называют вид нагружения, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — продольная сила.
Продольные силы меняются по длине бруса. При расчетах после определения величин продольных сил по сечениям строится график — эпюра продольных сил.
Условно назначают знак продольной силы.
Если продольная сила направлена от сечения, то брус растянут. Растяжение считают положительной деформацией (рис. 20.1а).
Если продольная сила направлена к сечению, то брус сжат. Сжатие считают отрицательной деформацией (рис. 20.16).
56. Эпюра— график, дающий величину продольной силы в каждом поперечном сечении.
58.Закон Гука для растяжения (сжатия)
Закон Гука справедлив лишь в определенных пределах нагрузки. Нормальное напряжение прямо пропорционально относительному удлинению или укорочению. Е – коэффициент пропорциональности (модуль продольной упругости) характеризует жесткость материала, т.е. способность сопротивляться упругим деформациям растяжения или сжатия.
Связь между силой упругости и упругой деформацией тела (при малых деформациях) была установлена Гуком. Математическое выражение закона Гука для деформации одностороннего растяжения (сжатия) имеет вид
где f — сила упругости; х — удлинение (деформация) тела; k — коэффициент пропорциональности, зависящий от размеров и материала тела, называемый жесткостью. Единица жесткости в СИ — ньютон на метр (Н/м).
Закон Гука для одностороннего растяжения (сжатия) формулируют так: сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела.
59. Характеристики прочности
1. Предел пропорциональности Опц = Fпц / Ao — наибольшее напряжение растяжения, при котором еще справедлив закон Гука. Здесь Fпц — нагрузка, определяемая по отклонению диаграммы (рис. 6, а) от первоначального прямолинейного участка.
2. Предел упругости Oу = Fy / Ao — представляет собой напряжение, при котором остаточные деформации незначительны (0,001 — 0,003 %).
Практически можно считать предел упругости совпадающим с пределом пропорциональности.
3. Предел текучести От = Fт / Ao — напряжение, при котором наблюдается рост деформаций при постоянной нагрузке.
4. Предел прочности или временное сопротивление материалов Oв = Fmax / Ao — напряжение, вызванное наибольшей нагрузкой.
5. Истинное сопротивление разрыву Sk = Fk / Ak — напряжение, определяемое отношением нагрузки Fк в момент разрыва к площади поперечного сечения образца в месте разрыва.
60. Условие прочности при растяжении сжатии
Условие прочности при растяжении (сжатии) выражается неравенством:
где [σ] – допускаемые напряжения, определяются как:
n – коэффициент запаса прочности, устанавливаемый нормативными документами.
Условие прочности позволяет решать три типа задач:
1. Проверка прочности (проверочный расчет)
2. Подбор сечения (проектировочный расчет)
3. Определение грузоподъемности (допускаемой нагрузки)
61. Расчет на прочность при растяжении или сжатии.
Для обеспечения прочности расчетное напряжение не должно превышать допускаемого напряжения.
1. Проверочный расчет- известно нагрузки, материал, размеры детали: необходимо проверить, обеспечена ли прочность.
2. Проектировочный расчет- задана расчетная схема и нагрузки: материал или размеры детали подбираются.
3. Определение нагрузочной способности( максимальной нагрузки)
62.Срез: основные расчетные предпосылки, расчетные формулы.

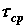


При расчете болтов, штифтов, шпонок и прочего принимают 
63. Смятие: условности расчета, расчетные формулы.

где F/i — нагрузка на один соединительный элемент (i — число элементов); 


Если поверхность смятия плоская, как, например, при соединении вала 1 и втулки 2 призматической шпонкой 3 (рисунок справа), то площадь смятия определяется непосредственно как произведение длины на ширину: 
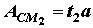
Если поверхность смятия цилиндрическая, то в расчетную формулу подставляется условная площадь смятия, равная площади проекции поверхности на диаметральную плоскость. На рисунке слева условная площадь смятия 
64.Расчеты на срез и смятие болтовых и заклепочных соединений.
болтовом или заклепочном соединении внешние усилия пытаются сдвинуть соединяемые элементы в противоположные стороны, но болты или заклепки препятствуют этому. В результате этого в месте соединения элементов болт или заклепка работают на срез, а в месте соединения заклепки с элементом происходит смятие болта или заклепки.
Иногда болты или заклепки работают на растяжение. В этом случае решается вопрос о том, на сколько выдержит отрыв головка заклепки или болта. В заклепочных и болтовых соединениях при действии на соединение продольной силы N (в стыках или прикреплениях элементов) распределение этой силы между заклепками или болтами принимается равномерным.
Заклепочные или болтовые соединения (см. рис. 21), воспринимающие продольные силы N, рассчитываются по формулам:
где N — расчетная продольная сила, действующая на соединение, кН; n – число заклепок или болтов в соединении; F – площадь среза, см2; nср – число рабочих срезов одной заклепки или болта; d – диаметр отверстия для заклепки или наружный диаметр стержня болта; Σδ – наименьшая суммарная толщина элементов, сминаемых в одном направлении; R_ср^б, R_ср^закл — расчетное сопротивление снятию болтовых или заклепочных соединений; R_р^б, R_р^закл — расчетное сопротивление растяжению (отрыву головок) болтов или заклепок; Fн – площадь болта см2.
Источник