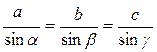Последовательность решения задачи
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СТЕРЖНЕЙ
Последовательность решения задачи
1.Выбрать тело (точку), равновесие которого следует рассматривать.
2.Освободить тело (шарнир В) от связей и изобразить действующие на него силы и реакции отброшенных связей. Причем реакции стержней следует направить от шарнира В, так как принято предлагать, что стержни растянуты.
3.Выбрать оси координат и составить уравнения равновесия, используя условия равновесия системы сходящихся сил на плоскости.
Выбирая оси координат, следует учитывать, что полученные уравнения будут решаться проще, если одну из осей направить перпендикулярно одной из неизвестных сил.
4.Определить реакции стержней из решения указанной системы уравнений.
5.Проверить правильность полученных результатов, решив уравнения равновесия относительно заново выбранных координат Х и У.
Пример.Определить реакции стержней, удерживающих грузы
F1=70 кН и F2=100 кН (рис. 1). Массой стержней пренебречь.
Рис. 1 — Схема задачи
1. Рассматриваем равновесие шарнира В (рис. 1).
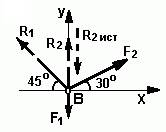
2. Освобождаем шарнир В от связей и изображаем действующие на него активные силы и реакции связей (рис. 2).
3. Выбираем систему координат, совместив ось У по направлению с реакцией R2 (рис. 2) и составляем уравнения равновесия для системы сил, действующих на шарнир В:
Рис. 2 — Выбор систем координат
4. Определяем реакции стержней R1 и R2 решая уравнения.
Из уравнения ( 1 ) получаем
Подставляя найденное значение R1 в уравнение ( 2 ), получаем
R2 = F1 — F2 × cos 60° — R1 × cos 45° = 70 — 100× 0,5 — 122 × 0,707 = — 66,6 кН
Знак минус перед значением R2 указывает на то, что первоначально выбранное направление реакции неверное — следует направить реакцию R2 в противоположную сторону, то есть к шарниру В (на рис. 3 истинное направление реакции R2 показано штриховым вектором).
Рис. 3 — Истинное направление реакций
5. Проверяем правильность полученных результатов, выбрав новое расположение осей координат Х и У (рис. 4). Относительно этих осей составляем уравнения равновесия:

Рис. 4 — Выбор систем координат
Подставляем значения реакций R1 и R2, полученные при решении уравнений (1) и (2), в уравнения (3) и (4).
Условия равновесия å Fi х = 0;å Fi у = 0 выполняется следовательно, задача решена правильно.
Задача. Определить реакции стержней, удерживающих грузы F1 и F2. Массой стержней пренебречь. Схему своего варианта смотри на рисунке 5. Числовые данные своего варианта взять из таблицы 1.
Источник
Решение задач на равновесие геометрическим способом
Геометрическим способом удобно пользоваться, если в системе три силы. При решении задач на равновесие тело считать абсолютно твердым (отвердевшим).
Порядок решения задач:
1. Определить возможное направление реакций связей.
2. Вычертить многоугольник сил системы, начиная с известных сил в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура.)
3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
4. Для уточнения решения рекомендуется определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.
Решение задач на равновесие плоской системы
Сходящихся сил аналитическим методом
Непосредственное применение условий равновесия в геометрической форме дает наиболее простое решение для системы трех сходящихся сил. При наличии в системе четырех и более сил рациональнее применять аналитический метод, который является универсальным и применяется чаще всего. При аналитическом методе решение этих задач выполняется на основе уравнений равновесия по следующему плану:
первый этап — выделяют объект равновесия тело или точку, где пересекаются линии действия всех сил, т. е. точку, равновесие которой в данной задаче следует рассмотреть;
второй этап — к выделенному объекту равновесия прикладывают заданные силы;
третий этап — выделенную точку или тело освобождают от связей, их действие заменяют реакциями;
четвертый этап — выбирают координатные оси и составляют уравнения равновесия;
пятый этап — решают уравнения равновесия;
шестой этап — проверяют правильность решения.
В задачах статики часто приходится определять реакции стержней. Необходимо установить, как действуют растягивающие и сжимающие силы в стержнях на точки крепления стержней или узлы. Когда стержень MN растянут
(рис. 5, а), его реакции на точки крепления направлены от этих точек М и N
внутрь стержня. Когда стержень сжат, его реакции направлены к точкам закрепления, т, е. наружу (рис, 5, б). Следовательно, можно сказать, что в растянутом стержне реакции направлены от узлов внутрь стержня, в сжатом к узлам наружу от стержня, по аналогии с деформированной пружиной.
Часто при решении задач трудно заранее определить направление реакций стержней. В этих случаях удобно считать стержни растянутыми и их реакции направлять от узлов.
Если решение задачи даст значение реакции со знаком минус, то в действительности имеет место не растяжение, а сжатие. Таким образом, реакции растянутых стержней будут положительными, а сжатых — отрицательными.
Пример 1. Груз подвешен на стержнях и находится в равновесии. Определить усилия в стержнях (рис. 6а).
1. Усилия, возникающие в стержнях крепления, по величине равны силам, с которыми стержни поддерживают груз (5-я аксиома статики) (рис.6а).
Определяем возможные направления реакций связей «жесткие стержни».
Усилия направлены вдоль стержней.
2. Освободим точку А от связей, заменив действие связей ихреакциями
3. Система находится в равновесии. Построим треугольник сил. Построение начнем с известной силы, вычертив вектор F в некотором масштабе.
Из концов вектора F проводим линии, параллельные реакциям
Пересекаясь, линии создадут треугольник (рис. 6в). Зная масштаб построений и измерив длину сторон треугольника, можно определить величину реакций в стержнях.
4. Для более точных расчетов можно воспользоваться геометрическими соотношениями, в частности теоремой синусов: отношение стороны треугольника к синусу противоположного угла — величина постоянная
Для данного случая:

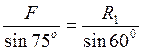




З а м е ч а н и е. Если направление вектора (реакции связи) на заданной схеме и в треугольнике сил не совпало, значит, реакция на схеме должна быть направлена в противоположную сторону.
Пример 2. Решение задач на равновесие плоской системы сходящихся сил
Дано: Груз подвешен на стержнях и канатах и находится в равновесии. Определить реакции стержней АВ и ВС. (рис. 7).
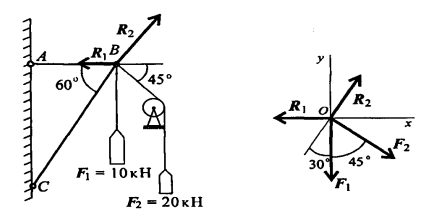
1. Определим вероятные направления реакций. Мысленно убираем стержень АВ, при этом стержень СВ опускается, следовательно точка В отодвигается от стены: назначение стержня АВ — тянуть точку В к стене.
Если убрать стержень СВ, точка В опустится, следовательно, стержень СВ поддерживает точку В снизу — реакция направлена вверх.
2. Освободим точку В от связей.
Пример 3. К кронштейну АВС в точке В подвешены два груза: груз g1 — 600 Н непосредственно и груз g 2 = 400 Н через отводной блокD (рис. 9, а). Определить реакции стержней АВ и ВС кронштейна.
В точке В пересекаются линии действия заданных сил G 1 и G 2 и искомых реакций стержней АВ и СВ, поэтому выделяем узел В (рис. 8, б), который в данной задаче рассматривается как объект равновесия. Прикладываем к этому узлу заданные силы G 1, направленную вертикально, и G 2, направленную вдоль троса. При этом учитываем, что неподвижный блок D изменяет направление силы, но не влияет на ее значение. Освобождаем узел В от связей, которые осуществляются стержнями АВ и ВС. Прикладываем вместо них реакции стержней ri и R 2, направляем их вдоль стержня от узла, т. е. полагаем, что оба стержня АВ и ВС растянуты. Выбираем координатные оси х и у (при выбранном направлении осей большинство проекций имеют знак плюс) и составляем уравнения равновесия:
1). Σ Fix = 0; R 1- G2 cos 45° + R2 cos 45° = 0;
Решив уравнения равновесия, находим:
R 1 = G2cos45° — R 2соз45° = 400 · 0,707 — (-1249) 0,707 = 1166 Н.
Знак минус перед численным значением реакции R2показывает, что стержень ВС не растянут, как предполагалось, а сжат.
Задание 1
1  | 2  |
3  | 4  |
5  | 6  |
7  | 8  |
9 F1  F2 F2 | 10 F1  F2 F2 |
Таблица1 –Данные по вариантам
| Вариант | № схемы | F1 | F2 | Вариант | № схемы | F1 | F2 |
| 1 | 1 | 6 | 7,4 | 16 | 6 | 7 | 9 |
| 2 | 2 | 4,2 | 10 | 17 | 7 | 11 | 6,2 |
| 3 | 3 | 8 | 6,2 | 18 | 8 | 14 | 8,4 |
| 4 | 4 | 12 | 12 | 19 | 9 | 8,5 | 10 |
| 5 | 5 | 3 | 12,6 | 20 | 10 | 7,2 | 7 |
| 6 | 6 | 4.5 | 10 | 21 | 1 | 10 | 6.5 |
| 7 | 7 | 4,6 | 7,2 | 22 | 2 | 6,8 | 4,6 |
| 8 | 8 | 8.2 | 11 | 23 | 3 | 12 | 5.2 |
| 9 | 9 | 5,4 | 6,8 | 24 | 4 | 13,6 | 8,4 |
| 10 | 10 | 4,8 | 7 | 25 | 5 | 14 | 6,8 |
| 11 | 1 | 9 | 11 | 26 | 6 | 12,6 | 9 |
| 12 | 2 | 11 | 14 | 27 | 7 | 14 | 12 |
| 13 | 3 | 5 | 8,5 | 28 | 8 | 7,5 | 5,8 |
| 14 | 4 | 12 | 7,2 | 29 | 9 | 9,8 | 10,5 |
| 15 | 5 | 14 | 10 | 30 | 10 | 14 | 12 |
Контрольные вопросы
1. Определить модуль равнодействующей системы сходящихся сил, если проекции слагаемых векторов равны: Flx = 50 Н; F2x = -30 Н; F3x = 60 Н; F4x = 70 Н;
2. В каком из указанных случаев плоская система сходящихся сил уравновешена?
3. Какая из приведенных ниже систем уравнений равновесия справедлива для изображенной на рис.9 системы сходящихся
4. По изображенным многоугольникам сил (рис. 10) решите, сколько сил входит в каждую систему, и какая из них уравновешена. (Обратить внимание на направление векторов.)

Практическое занятие № 02
Тема : Определение опорных реакций балок
Цель: Научиться составлять расчетные схемы балок и определять их опорные реакции.
Входной контроль
1. Пара сил и ее действие на тело.
2. Шарнирно-подвижная опора
3. Жесткая заделка (защемление)
Теоретический материал
Виды нагрузок
По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосредоточенной.
Часто нагрузка распределена по значительной площадке или линии (давление воды на плотину, давление снега на крышу и т.п.), тогда нагрузку считают распределенной.
В задачах статики для абсолютно твердых тел распределенную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 1).
q — интенсивность нагрузки; l — длина стержня;
G = ql равнодействующая распределенной нагрузки.
Дата добавления: 2020-04-08 ; просмотров: 3886 ; Мы поможем в написании вашей работы!
Источник