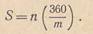Определение размеров земли способы

Методы определения формы и размеров Земли

Астрономо-геодезический метод. Определение формы и размеров Земли при помощи этого метода основано на использовании градусных измерений, суть которых сводится к определению линейной величины дуг меридианов и параллелей на разных широтах.

Первое известное в истории определение длины земного меридиана, выполненное в античное время в Египте принадлежит Эратосфену. По его определениям длина меридианной окружности, равнялась 39 500 км, то есть очень близко к действительной величине меридиана 40 009 км. Ряд допущений, сделанных Эратосфеном, и несовершенный метод линейных измерений (расстояние определялось по длине караванного пути, измеренное в египетских стадиях (1 стадия может быть приравнена к 157,5 м) привели к приближенным результатам. Однако значение выполненных работ заключается в том, что Эратосфен впервые применил геодезический метод определения размеров Земли и получил довольно удовлетворительные для того времени результаты.

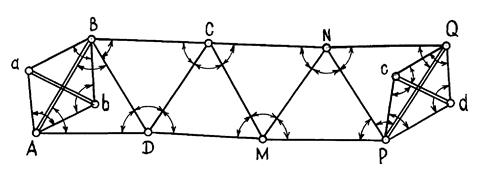
Высокая точность измерения значительных по протяженности расстояний обеспечивается методом триангуляции, который был разработан в 1615 г. голландским ученым В. Снеллиусом. Триангуляция (от лат. triangulum – треугольник) – способ определения положения опорных геодезических пунктов А, В, С,… на местности путем построения сети примыкающих друг к другу треугольников, в которых измеряются все углы, а с помощью базиса аb определяется длина выходной стороны АВ в их ряду, длины же других сторон вычисляют по координатам этих пунктов (рис. 2.3).

Триангуляция являлась основным способом создания опорной геодезической сети и градусных измерений до развития и становления космического метода. Триангуляционные работы по определению длины дуг меридианов и параллелей проводились учеными разных стран (см. п. 1.2 и 2.1).

Геофизический (гравиметрический) метод. Геофизика – это наука, изучающая физические свойства Земли в целом и процессы, происходя­щие в ее геосферах. Этот метод основан на измерении величин, характе­ризующих земное поле силы тяжести, и их распределение на по­верхности Земли. Измерения потенциала силы тяжести, выполняемые на поверхности Земли, позволяют вычислять сжатие Земли с большей точностью, чем астрономо-геодезическим методом.

Преимуществом этого метода является то, что его можно использо­вать на акваториях морей и океанов, где возможности астрономо-геодезического метода ограничены. С именем французского ученого А. Клеро (1713–1765) связано применение гравиметрического метода. В 1743 г. предполагая, что Земля состоит из сфероидальных слоев с общим центром, плотность которых возрастает к центру, он получил формулу для вычисления ускорения силы тяжести в любой точке Земли:

,

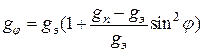
где g_φ ; g_э; g_n – ускорение силы тяжести, соответственно, на определяемой широте φ, на экваторе и на полюсе. Если в имеющуюся формулу подставить числовые значения g_э и g_n , полученные путем измерений, то формула примет вид: g _φ = 978, 030 (1+ 0,005302 sin 2 φ).

Развитие космического метода относится к периоду освоения космического пространства с помощью ИСЗ. Этот метод основан на наблюдениях за ИСЗ и определении координат в заданный момент времени. Выявление отклонений реальных орбит ИСЗ от предвычисленных, вызванных неравномерным распределением масс в земной коре, позволяет уточнить представление о гравитационном поле Земли, а, следовательно, о ее форме и размерах (см. п. 7.5).

Дата добавления: 2016-04-11 ; просмотров: 1444 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Определение формы и размеров Земли

1. Шарообразность Земли. Часто для доказательства шарообразности Земли приводят явления, которые в действительности подтверждают лишь выпуклость или искривленность ее поверхности. Таким доказательством кривизны земной поверхности является, например, то, что при приближении корабля к берегу сперва показываются из-за горизонта вершины мачт, а потом уже его корпус.

Кругосветные путешествия подтверждают только замкнутость формы Земли, ее изолированность в пространстве, отсутствие у нее краев, где-либо смыкающихся с небом.

Наглядными доводами в пользу шарообразности Земли можно считать такие явления:

а) в любом месте Земли открытый горизонт представляется окружностью и дальность горизонта на уровне моря всюду одинакова;

б) во время лунных затмений тень Земли, падающая на Луну, всегда имеет округлые очертания. Из всех тел только шар при любом положении отбрасывает круглую тень.

Фотографии края Земли, полученные с ракет, запущенных на большую высоту, и фотографии, полученные первыми советскими космонавтами Гагариным и Титовым, показывают, что всякий край Земли представляет собой отрезок окружности. Точнее форма и размеры Земли вычисляются с помощью градусных измерений.

2. Определение размеров Земли. Определение размеров Земли состоит в том, что по меридиану измеряют некоторую дугу — в линейных мерах и в градусах. Между двумя пунктами земного шара, находящимися на одном меридиане, определяют линейное расстояние, равное, положим, n километрам.

Определяют также разность географических широт этих пунктов астрономическим способом (например, по разности высот Полярной звезды в этих пунктах). Пусть эта разность составляет т градусов.

Тогда частное m/360 покажет, какую часть окружности представляет собой ее дуга между пунктами. На этом основании находят длину всей окружности в километрах из простого соотношения:

Описанный способ называется градусным измерением. Зная длину земной окружности, делением ее на 2pi получают длину радиуса Земли. Таким образом было установлено, что радиус Земли, если ее считать шаром, равен 6371 км, а длина окружности — почти 40 000 км.

Большие градусные измерения были выполнены в прошлом столетии русскими учеными под руководством В.Я. Струве. В наше время большие измерения дуг на поверхности Земли выполнены в СССР.

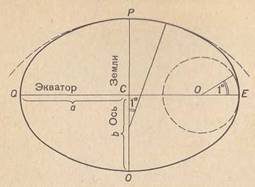
3. Сжатие Земли. Измерения в разных местах Земли показали, что кривизна Земли у экватора больше, чем у полюсов (Рисунок 24). Это означает, что Земля не шар; она немного сжата вдоль оси вращения. Полярный радиус Земли короче экваториального почти на 21 км, то есть приблизительно на 1/300 экваториального радиуса.

Рисунок 24 — Кривизна Земли у экватора больше, чем у полюсов.

Сжатие Земли есть результат действия центростремительной силы, возникающей при вращении Земли вокруг оси. Сжатие может быть продемонстрировано вращением тонкого стального обруча на оси школьной центробежной машины. Сжатие небесного тела вследствие его вращения является общим правилом. Например, планеты Юпитер и Сатурн, вращающиеся вокруг оси быстрее, чем Земля, сжаты еще заметнее. Вследствие сжатия фигура Земли не шар, а эллипсоид вращения. Представление о фигуре Земли значительно уточнено советскими учеными. Оказывается, что истинная фигура Земли очень сложной формы, даже если отвлечься от таких неровностей ее, как горы.

Источник

1. Способы определения формы и размеров Земли. Общие сведения о форме и размерах Земли.

Астрономо-геодезический (геометрический) метод – определение фигуры и размеров Земли основано на использовании градусных измерений, суть которых сводится к определению линейной величины одного градуса дуги меридиана и параллели на разных широтах. Однако непосредственные линейные измерения значительной протяжённости на земной поверхности затруднены, её неровности существенно снижают точность работ. Триангуляционный – высокая точность измерения значительных по протяженности расстояний. Метод разработал Снеллиус. Основы метода: 1 градус дуги меридиана у полюса длиннее, чем у экватора -> Земля имеет форму эллипсоида вращения, сплюснутого у полюсов. Геофизический (гравиметрический) метод – основан на измерении величин, характеризующих земное поле силы тяжести, и их распределении на поверхности Земли. Этот метод можно применять на акваториях морей и океанов. Данные измерений потенциала силы тяжести, выполненные на поверхности планеты, позволяют вычислить сжатие Земли с большей точностью, чем астрономо-геодезическим методом. Космический метод – освоение космического пространства: наблюдение за искусственными спутниками Земли (ИСЗ) на орбите и определение их пространственных координат в заданный момент времени, выявление отклонения реальных орбит ИСЗ от предвычисленных, вызванные неравномерным распределением масс в земной коре, позволяют уточнить представление о гравитационном поле Земли и конечном счёте о её фигуре. Фигура Земли формируется под влиянием внутренних и внешних сил. Основными являются сила внутреннего тяготения и центробежная сила. По данным геофизики Земля ведет себя как пластичное тело. Если бы она была неподвижным и однородным по плотности телом, то под действием только сил внутреннего тяготения она, как фигура равновесия, имела бы форму шара. Вследствие центробежной силы, вызванной вращением вокруг оси, Земля приобрела бы форму шара, сплюснутого с полюсов, то есть форму эллипсоида вращения с малой степенью сжатия в направлении полюсов. На самом деле внутреннее строение Земли по плотности неоднородно. В результате процессов, связанных с образованием и жизнью нашей планеты, вещество Земли распределяется, в общем, концентрическими слоями, плотность которых возрастает от поверхности к центру. При таком строении Земля также должна была бы иметь фигуру эллипсоида, но с другой степенью сжатия, нежели при однородной плотности. В обоих случаях поверхность тела, находящегося в состоянии гидростатического равновесия, будет всюду горизонтальна, поскольку в каждой точке направление силы тяжести (отвесной линии) совпадает с нормалью (перпендикуляром) к поверхности. Поверхности, нормальные в каждой точке к отвесной линии, называются уровенными поверхностями силы тяжести. Таким образом, поверхность эллипсоида вращения будет уровенной. Однако земная кора (наружный слой земли толщиной в среднем 40 км) состоит из неоднородных по плотности участков: материки и океанические впадины сложных геометрических форм, равнинные и гористые формы рельефа материков и соседствующих с ними океанов и морей. Вследствие такого неравномерного распределения масс в земной коре изменяются направления сил притяжения, а значит, и сил тяжести. При этом уроненная поверхность, как перпендикулярная к направлениям силы тяжести, отступает от эллипсоидальной и становится столь сложной и неправильной в геометрическом отношении, что ее форму нельзя описать конечным математическим выражением. Фигуре Земли, образованной уроненной поверхностью, совпадающей с поверхностью океанов и морей и мысленно продолженной под материками, присвоено название геоид. Для математической обработки результатов геодезических измерений нужно знать форму поверхности Земли. Использовать для этой цели физическую поверхность 5 или поверхность геоида 4 нельзя вследствие их сложности. Поскольку наибольшие отступления геоида от эллипсоида не превышают 100—150 м, фигурой, наиболее близкой к геоиду, является эллипсоид вращения, называемый земным эллипсоидом. Параметрами, определяющими его размеры и форму, являются большая а и малая b полуоси или большая полуось а и полярное сжатие α = (а — b)/а. Величины этих параметров могут быть получены посредством градусных измерений, т. е. путем геодезических измерений длины дуги меридиана в 1°. Зная длину градуса в различных местах меридиана, можно установить фигуру и размеры Земли. Параметры земного эллипсоида неоднократно определялись учеными различных стран. В 1946 г. для геодезических и картографических работ в СССР приняты следующие размеры земного эллипсоида: а = 6 378 245 м, b — 6 356 863 м, α = 1: 298,3. Эти параметры получены в 1940 г. выдающимся советским геодезистом Ф. Н. Красовским. Чтобы максимально приблизить поверхность земного эллипсоида к поверхности геоида, эллипсоид соответствующим образом ориентируют в теле Земли. Такой эллипсоид называют референц-эллипсоидом. В практике инженерно-геодезических работ поверхности эллипсоида и геоида считают совпадающими, во многих случаях значительные по размерам участки земной поверхности принимают даже за плоскость, а при необходимости учета сферичности Земли считают ее шаром, равным по объему земному эллипсоиду. Радиус такого шара равен 6371,11

2. Связь топографии с другими науками. Топография теснейшим образом связана с географическими науками – ландшафтоведением, геоморфологией, гидрологией; с картографией; с фотограмметрией (наука, изучающая способы измерения объектов земной поверхности и определения их координат по фотоизображениям); очевидна связь с геодезическим приборостроением; методы решения научных и практических задач основаны на законах физики и математики; в основе автоматизации процессов создания топографических карт лежат достижения кибернетики и вычислительной техники. Продукция картографо-геодезического производства широко используется другими науками, а также многими отраслями хозяйства. Общая задача картографии, геодезии и топографии – обеспечение хозяйством, научных исследований, вооруженных сил страны геодезическими данными и современными географическими картами. Каждая из этих наук решает свои определенные задачи. Топография – это наука, изучающая физическая земную поверхность в геометрическом отношении. Топография занимается измерениями на земной поверхности или по аэрофотоснимкам с целью составления графических изображений земной поверхности: планов, топографических карт и профилей. Топография наиболее тесно связана с географическими науками. Это объясняется тем, что для составления карт, планов, профилей необходимо не только изучить данную территорию в геометрическом отношении, но и знать существо тех объектов, которые изображены на топографической карте, т.е. необходимо знание данной территории в географическом отношении. Без знания географических особенностей территории, даже при точных данных геометрических исследований, нельзя отразить географическую природу поверхности. Топография связана с фотограмметрией, которая занимается методами измерений объектов земной поверхности по их фотоизображению на снимках (воздушных, космических, наземных). Топография связана с электроникой, кибернетикой и рядом других наук, поэтому она является прикладной математической наукой. В свою очередь топография создает материалы, в которых нуждается многие науки.

3. Методы проектирования земной поверхности на поверхность относимости – уровенную поверхность и плоскость Проекция – способ передачи изображения земной поверхности на плоскость, основанный на математических зависимостях.

О 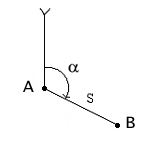ртогональный метод – основной метод проектирования земной поверхности – проектирование на уровенную поверхность осуществляется отвесными (вертикальными) линиями, соответствующими направлениям силы тяжести. Центральная проекция – проектирование производится линиями, исходящими из одной точки (центра проекции). Проектирование – это способ передачи взаимного расположения объектов земной поверхности на поверхность относимости с использованием математических зависимостей. Поверхность относимости: уровенная поверхность, плоскость.

Основной метод проектирования: метод ортогонального проектирования. В топографии и геодезии проектирование ведётся отвесными линиями. Ввиду малого отклонения направление нормалей можно считать совпадающими с направлением отвесных линий. Полученные проекции – горизонтальные – гориз-ая пов-ть — пов-ть, перпендикулярная в каждой точке направления отвесной линии. При проектировании небольших участков земной пов-ти часть уровенной пов-ти можно заменить плоскостью. В этом случае отвесные линии практически параллельны между собой и горизонтальная проекция земной пов-ти преобразуется в ортогональную проекцию – проекция, полученная параллельными проектирующими линиями, перпендикулярными плоскости проектирования. Горизонтальное проложение — проекция линии местности на горизонтальную плоскость (S — s). Таким образом, положение точек и линий местности в ортогональной проекции определяется длинами горизонтальных проложений s, t и горизонтальными углами β. Горизонтальные проложения линий отличаются от их длин на местности. Это различие можно вычислить по известным формулам тригонометрии. Пр., s=S cos v.Угол v – вертикальный угол – он характеризует отклонение земной пов-ти на конкретном участке от горизонтальной пл-ти. Центральная проекция – проектирование производится линиями, исходящими из одной точки А – центра проекции. Чтобы перейти от изображения значительной по площади территории земной пов-ти в горизонтальной проекции к её плоскому изображению на карте, применяют картографические проекции.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник