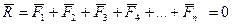Техническая механика. Шпаргалка
Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.
Оглавление
- 1. Аксиомы и понятие силы статики
- 2. Связи и реакции связей
- 3. Определение равнодействующей геометрическим способом
- 4. Определение равнодействующей аналитическим способом
- 5. Пара сил. Момент силы
Приведённый ознакомительный фрагмент книги Техническая механика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.
3. Определение равнодействующей геометрическим способом
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.
Необходимо определить равнодействующую системы сходящихся сил (F1; F2; F3;…; Fn), где n — число сил, входящих в систему.
В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.
Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.
Многоугольник сил строится в следующем порядке.
1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.
2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.
3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.
Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.
Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.
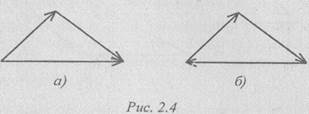
Если в системе три силы, образуется треугольник сил.
Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).
Задачи решаются в следующем порядке.
1. Определить возможное направление реакций связей.
2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).
3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
4. Для уточнения определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.
Источник
Определение равнодействующей геометрическим способом
Геометрический способ заключается в построение силового многоугольника, аналитический – в определении суммы проекций всех действующих сил на две взаимноперпендикулярные оси.
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых.
Порядок построения силового многоугольника
1. Выбираем полюс построения.
2. Помещаем в полюс начало первого вектора F2 (векторы сил можно вычерчивать в любом порядке) переместив его параллельно самому себе, сохранив его величину.
3. Помещаем в конец первого вектора начало второго F1 . Вычерчиваем один за другим в аналогичном порядке векторы остальных сил F4 , F3.
4. Вектор равнодействующей замыкает полученную ломаную линию;он соединяет начало первого вектора с концом последнего и направлен ему навстречу.
При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.
Рекомендация. Обратить внимание на направление векторов.
Геометрическое условие равновесия ПССС: силовой многоугольник должен быть замкнут.
Определение равнодействующей аналитическим способом
Модуль (величину) равнодействующей определяют по известным проекциям:
Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующей с осями координат (рис. 3.5).
Проекция силы на ось
Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца вектора
Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси. Таким образом, проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси (рис. 3.2).
Аналитическое условие равновесия ПССС: суммы проекций всех сил на две взаимноперпендикулярные оси должны быть равны нулю.
В задачах координатные оси выбирают так, чтобы решение было наиболее простым. Желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.
Тема 1.3. Плоская система произвольно расположенных сил
Момент силы относительно точки
Сила, не проходящая через точку крепления тела, вызывает вращение тела относительно точки, поэтому действие такой силы на тело оценивается моментом.
Момент силы относительно точки численно равен произведению модуля силы на плечо.
Плечо – кратчайшее расстояние от точки до линия действия силы (перпендикуляр, опущенный из точки на линию действия силы) (рис. 4.4).
Обозначение момента Mо(F) или mо(F); m0(F) = Fa.
Единица измерения mo(F) = Н·м.
Момент считается положительным, если сила пытается развернуть тело по часовой стрелке.
Момент силы относительно точки равен нулю, если линия действия силы проходит через точку, т. к. в этом случае расстояние от точки до силы равно нулю.
Плоская система произвольно расположенных сил
Главный вектор равен геометрической суммевекторов произвольной плоской системы сил. Проецируем все силы системы на оси координат и, сложив соответствующие проекции на оси, получим проекции главного вектора.
По величине проекций главного вектора на оси координат находим модуль главного вектора:
Главный момент системы сил равен алгебраической сумме моментов сил системы относительно точки приведения.
Таким образом, ПСПРС приводится к одной силе (главному вектору системы сил) и одному моменту (главному моменту системы сил).
Три формы условия равновесия ПСПРС
Для разных случаев используются три группы уравнений равновесия.
Для частного случая, если уравновешена система параллельных сил, можно составить только два уравнения равновесия:
Балочные системы. Определение реакций опор и моментов защемления
Виды нагрузок
По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосредоточенной.
Часто нагрузка распределена по значительной площадке или линии (давление воды на плотину, давление снега на крышу и т.п.), тогда нагрузку считают распределенной.
В задачах статики для абсолютно твердых тел распределенную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 6.1).
q
 |

q — интенсивность нагрузки, Н/м;
l— линия действия распределенной нагрузки, м;
Q = ql — равнодействующая распределенной нагрузки.
Разновидности опор балочных систем (см. реакции и их связи)Балка — конструктивная деталь в виде прямого бруса, закрепленная на опорах и изгибаемая приложенными к ней силами.
Высота сечения балки незначительна по сравнению с длиной. Жесткая заделка (защемление) (рис. 6.2)
Опора не допускает перемещений и поворотов. Заделку заменяют двумя составляющими силами RaxиRAy и парой с моментом MrА.
Для определения этих неизвестных удобно использовать систему уравнений в виде
Каждое уравнение имеет одну неизвестную величину и решается без подстановок. Для контроля правильности решений используют дополнительное равнение моментов относительно любой точки на балке, например В:
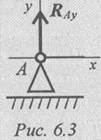
Шарнирно-подвижная опора (рис. 6.3).
Опора допускает поворот вокруг шарнира и перемещениевдоль опорной поверхности. Реакция направлена перпендикулярно опорной поверхности.
Шарнирно-неподвижная опора (рис. 6.4)
Опора допускает поворот вокруг шарнира и может быть заменена двумя составляющими силы вдоль осей координат.
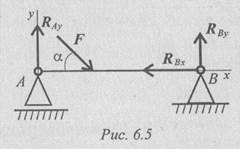
Балка на двух шарнирных опорах (рис. 6.5)
Тема 1.4. Центр тяжести
Сила тяжести — это сила, с которой тело притягивается к Земле, она распределена по всему объему тела.
Цент тяжести –это точка приложения силы тяжести.
Формулы для определения центра тяжести плоских фигур:
где Аn — площадь простейшей (элементарной) фигуры;
xn, yn — координаты центра тяжести простейшей (элементарной) фигуры.
Выражение 
Координаты центра тяжести сечения можно выразить через статический момент:
Оси, проходящие через центр тяжести, называются центральными осями. Статический момент относительно центральной оси равен нулю.
Источник
Геометрический способ определения равнодействующей плоской системы сходящихся сил.
Плоская система сходящихся сил – это такая система сил, в которой линии действия всех сил лежат в одной плоскости и все пересекаются в одной точке.
Любую плоскую систему сходящихся сил можно привести к одной силе, которая называется равнодействующей силой. Эта равнодействующая сила равна векторной сумме всех сил, входящих в систему.
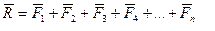
Проекции силы на оси координат.
Проекция силы на координатную ось – это отрезок оси, расположенный между двумя перпендикулярами, опущенными на ось из начала и конца вектора силы.
Если между линией действия силы F и осью х угол будет равен значению α, то проекции силы F на координатные оси будут равны:
Если вектор силы параллелен оси, то он проецируется на эту ось в натуральную величину, а если вектор силы перпендикулярен оси, то его проекция на эту ось равна нулю.
Аналитический способ определения равнодействующей плоской системы сходящихся сил.
Значение равнодействующей силы у плоской системы сходящихся сил аналитически вычисляется следующим образом:
1. Вычисляется сумма проекций всех сил системы на координатные оси х,у:
2. Вычисляется значение равнодействующей силы:
Условие равновесия плоской системы сходящихся сил.
1. Геометрическое условие равновесия – равнодействующая сила должна равняться нулю:
Сокращенно можно записать
2. Аналитическое условие равновесия – алгебраическая сумма проекций всех сил системы на координатные оси должна равняться нулю:
Названные выше уравнения называются уравнениями равновесия для плоской системы сходящихся сил.
Основная литература: 1;2
Дополнительная литература: 1;3
1. Дайте определение плоской системы сходящихся сил.
2. Дайте определение равнодействующей силы.
3. Каким образом геометрически вычисляется равнодействующая сила плоской системы сходящихся сил?
4. Что такое проекция силы на оси координат?
5. Каким образом вычисляются проекции силы на оси координат?
6. Каким образом аналитически вычисляется равнодействующая сила плоской системы сходящихся сил?
7. Назовите условия равновесия плоской системы сходящихся сил.
Лекция №4.
Цели занятия:
Рассмотреть распределённую нагрузку, где встречается распределённая нагрузка, каким образом рассчитываются конструкции при действии на них распределённых нагрузок.
План занятия:
1. Понятие распределённой нагрузки.
2. Примеры, где встречается распределённая нагрузка.
3. Равномерно распределённая нагрузка.
4. Приведение распределённой нагрузки к одной общей силе.
5. Неравномерно распределённые нагрузки.
Плоская система произвольно расположенных сил.
Распределённые нагрузки.
В природе часто встречаются силы, приложенные по поверхности тела. Такие силы называются распределёнными нагрузками.
Пространственные распределённые нагрузки характеризуются интенсивностью p (Н/м 2 ), на плоскости распределённые нагрузки характеризуются интенсивностью q (Н/м).
Интенсивность пространственной распределённой нагрузки можно перевести в интенсивность на плоскости по формуле
где b – ширина действия распределённой нагрузки.
Распределённые нагрузки бывают равномерно распределёнными и неравномерно распределёнными.
Равномерно распределённые нагрузки имеют постоянную интенсивность, неравномерно распределённые нагрузки имеют не постоянную интенсивность.
Рассмотрим равномерно распределённую нагрузку.
При расчётах распределённую нагрузку заменяют равнодействующей силой Q, которая будет приложена в середине участка, на котором действует распределённая нагрузка.
где l – длина действия распределённой нагрузки.
Рассмотрим неравномерно распределённые нагрузки.
1. Треугольная распределённая нагрузка.
У треугольной распределённой нагрузки равнодействующая сила Q равна:
2. Трапецеидальная распределённая нагрузка.
При расчетах трапецеидальную распределённую нагрузку распределяют на две распределённые нагрузки: прямоугольную и треугольную. Прямоугольную распределённую нагрузку заменяют равнодействующей силой Q1, а треугольную распределённую нагрузку заменяют равнодействующей силой Q2, которые будут равны:
Методом разделения сложной фигуры на две и более простые можно вычислить равнодействующие силы у других неравномерно распределённых нагрузок.
Существуют также криволинейные неравномерно распределённые нагрузки. Равнодействующие силы у таких распределённых нагрузок и точки их приложения вычисляются методами дифференциального и интегрального исчисления.
Основная литература: 1;2
Дополнительная литература: 1;3
1. Что такое распределённая нагрузка?
2. Чем характеризуется распределённая нагрузка?
3. Какие бывают распределённые нагрузки?
4. Что делают с распределёнными нагрузками при расчётах?
Лекция №5.
Цели занятия:
1. Рассмотреть понятие момента силы относительно точки, где в технике применяется момент силы.
2. Рассмотреть понятие пары сил, где в технике применяется пара сил.
Источник