Техническая механика. Шпаргалка
Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.
Оглавление
- 1. Аксиомы и понятие силы статики
- 2. Связи и реакции связей
- 3. Определение равнодействующей геометрическим способом
- 4. Определение равнодействующей аналитическим способом
- 5. Пара сил. Момент силы
Приведённый ознакомительный фрагмент книги Техническая механика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.
3. Определение равнодействующей геометрическим способом
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.
Необходимо определить равнодействующую системы сходящихся сил (F1; F2; F3;…; Fn), где n — число сил, входящих в систему.
В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.
Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.
Многоугольник сил строится в следующем порядке.
1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.
2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.
3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.
Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.
Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.
Если в системе три силы, образуется треугольник сил.
Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).
Задачи решаются в следующем порядке.
1. Определить возможное направление реакций связей.
2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).
3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
4. Для уточнения определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.
Источник
3. Определение равнодействующей геометрическим способом
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.
Необходимо определить равнодействующую системы сходящихся сил (F1; F2; F3;…; Fn), где n – число сил, входящих в систему.
В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.
Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.
Многоугольник сил строится в следующем порядке.
1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.
2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.
3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.
Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.
Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.
Если в системе три силы, образуется треугольник сил.
Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).
Задачи решаются в следующем порядке.
1. Определить возможное направление реакций связей.
2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).
3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
4. Для уточнения определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.
Данный текст является ознакомительным фрагментом.
Источник
Порядок решения задачи геометрическим способом
1. Выбрать масштаб построения многоугольника сил.
2. Вычертить многоугольник сил системы с помощью транспортира в масштабе складывая последовательно силы, входящие в систему, с соблюдением углов между векторами сил.
3. Измерить полученный вектор равнодействующей силы и определить его величину, учитывая выбранный масштаб.
4. Определить угол наклона равнодействующей силы к координатным осям.
Пример решения задачи
Определить равнодействующую плоской системы сходящихся сил аналитическим и геометрическим способами, если: F1=10кН; F2=15кН; F3=12кН; F4=8кН; F5=8кН; α1=30 0 ; α2=60 0 ; α3=120 0 ; α4=180 0 ; α5=300 0 .
| y |
Построим систему сходящихся сил по заданным направлениям векторов сил.
| F2 |
| F1 |
| F5 |
| F3 |
| F4 |
| x |
| α5 |
| α33333333333 |
| α2 |
| α1 |
Определим равнодействующую аналитическим способом, для чего найдем проекции заданных сил на координатные оси.
FΣ= 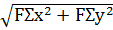
FΣ= 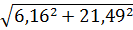
cos αΣx= 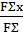
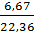
Определим равнодействующую графическим способом. С помощью транспортира в масштабе 2мм=1кН строим многоугольник сил (рис.2). Измерением определяем модуль равнодействующей силы и угол наклона ее к оси Ох.
Результаты расчета не должны отличаться более чем на 5%:
| F1 |
| F2 |
| F3 |
| F4 |
| F5 |
| FΣ |
| α x |
Содержание отчета:
1. Титульный лист в соответствии СТП 1.2-2005
4. Определение равнодействующей силы геометрическим и аналитическим способами
5. Ответы на контрольные вопросы
Контрольные вопросы:
1. Какие силы называются сходящимися?
2. Влияет ли порядок сложения сил на величину и направление равнодействующей?
3. Чему равна равнодействующая двух сил плоской системы сходящихся сил?
4. Можно ли менять порядок вычерчивания векторов в многоугольнике сил? Да, нет и почему?
5. Чем отличается равнодействующая данной системы сил от силы, уравновешивающей эту систему?
Практическая работа № 2
Тема:Решение задач на равновесие в аналитической форме
Цель работы: научиться решать задачи на равновесие в аналитической форме плоской системы сходящихся сил
Задание:
1. Определить величину и направление реакций связей по заданному варианту в аналитической форме.
2. Сделать проверку решения
3. Письменно ответить на контрольные вопросы
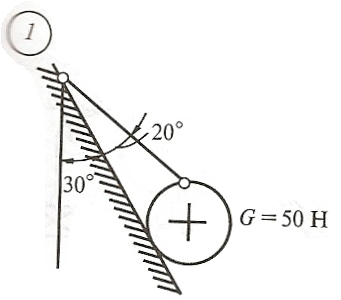
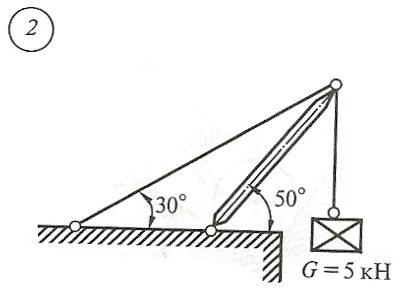
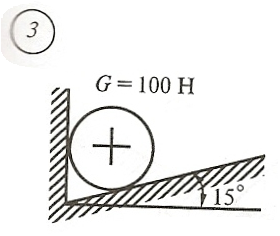
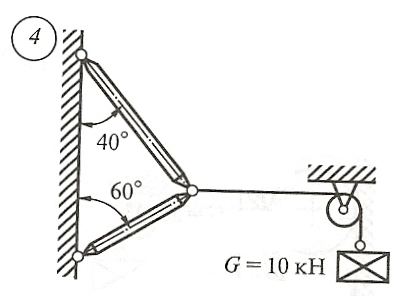
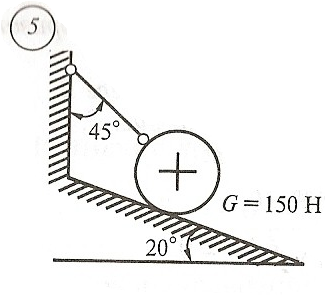
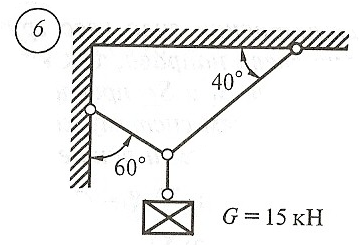
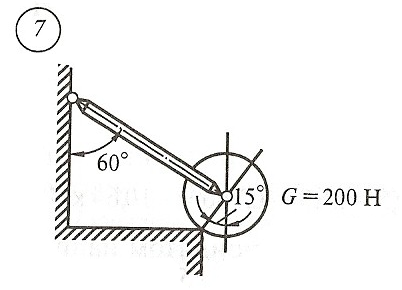
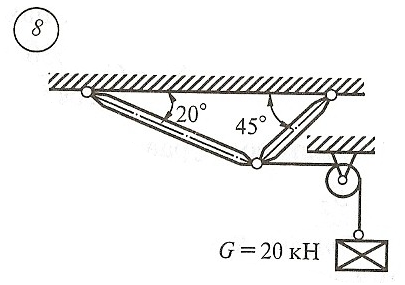
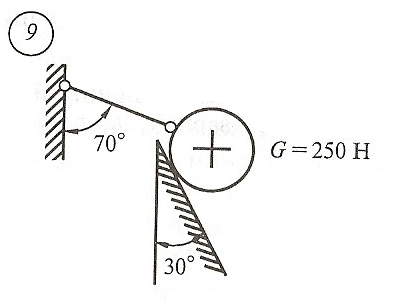
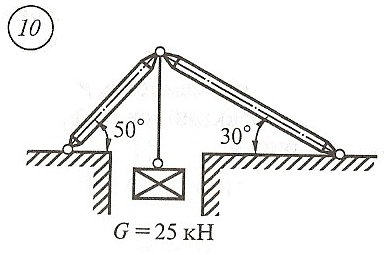
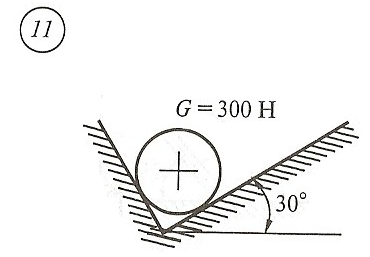
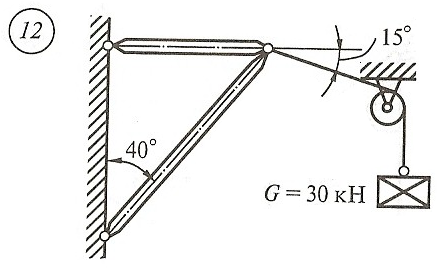
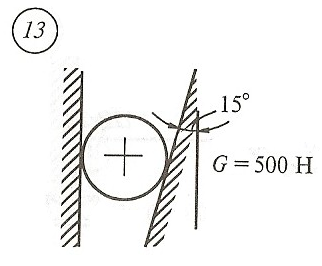
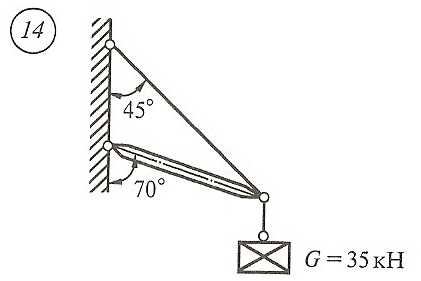
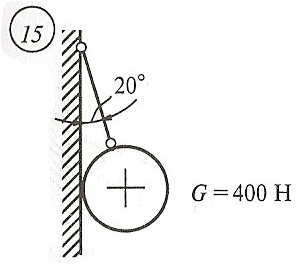
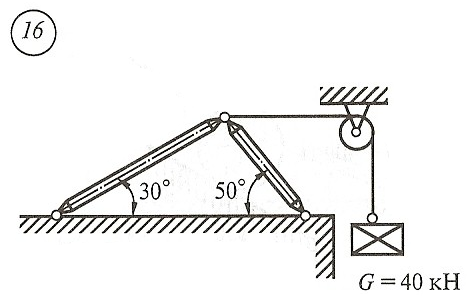
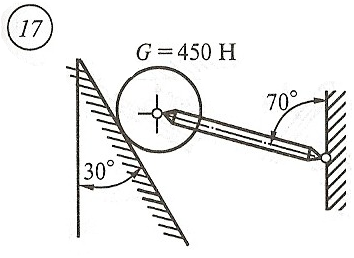
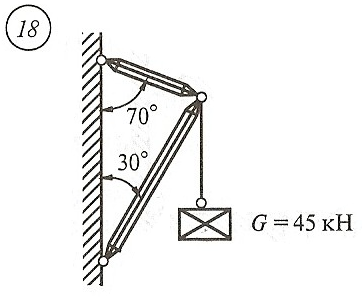
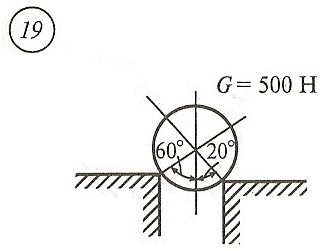
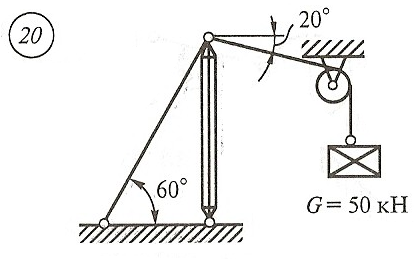
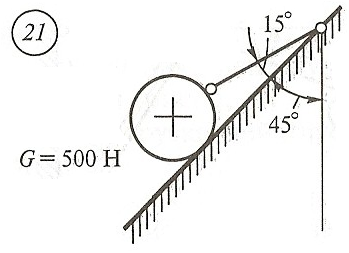
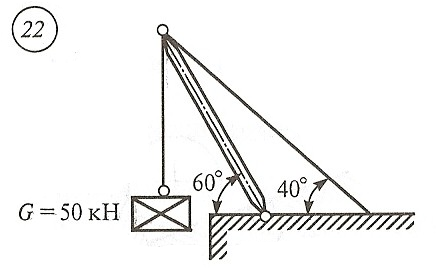
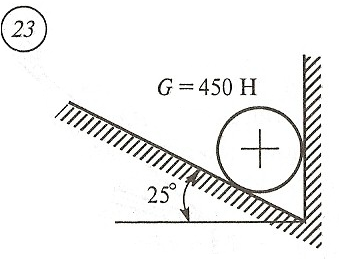
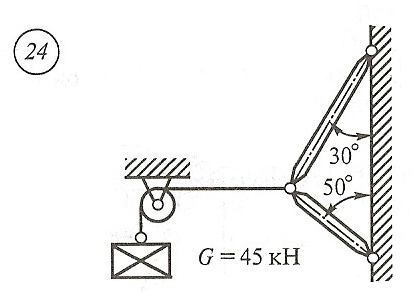
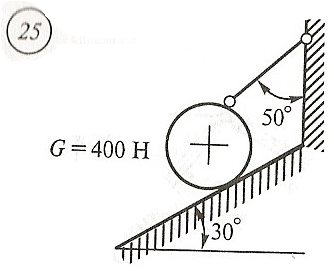
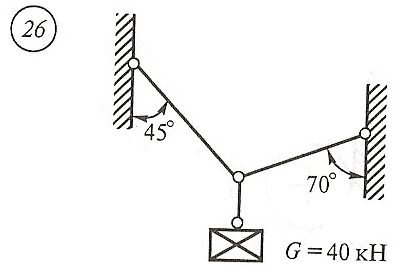
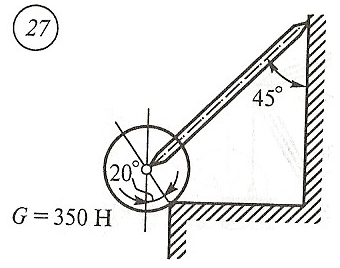
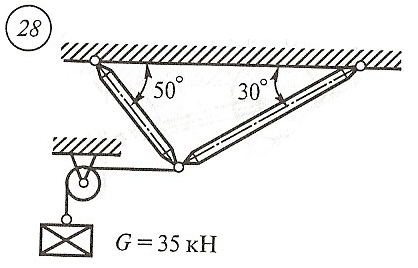
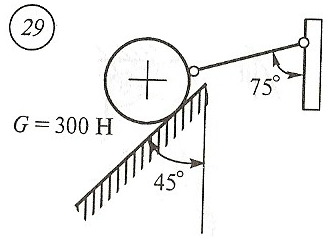
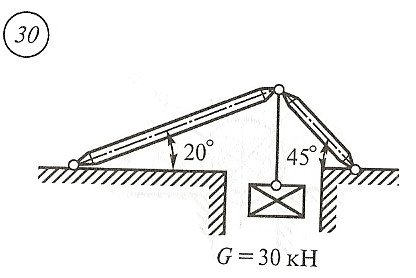
Схема задачи, величины углов и величина силы тяжести груза указаны в таблице 1 в соответствии с порядковым номером.
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Пояснения к работе:
Все законы и теоремы статики справедливы для свободного твердого тела.
Все тела делятся на свободные и связанные.
Свободные тела – тела, перемещение которых не ограничено.
Связанные тела – тела, перемещение которых ограничено другими телами.
Тела, ограничивающие перемещения других тел, называют связями.
Силы, действующие от связей и препятствующие перемещению, называют реакциями связей.
Реакция связи всегда направлена с той стороны, куда нельзя перемещаться.
Всякое тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).
Все связи можно разделить на несколько типов.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Источник









