Определение площади способом палетки

Измерение площадей палетками

Площади небольших участков с криволинейными граница­ми можно измерять с помощью палеток. Палетка для измере­ния площадей – лист прозрачного материала (восковки, лавса­на, пластика, кальки), на который нанесена сетка квадратов размером 2×2 мм или система равноотстоящих параллельных линий.

Наложив палетку с сеткой квадратов на план, подсчиты­вают число квадратов, уместившихся в измеряемой площади, оценивая дробные части квадратов на краях участка на глаз. Результат подсчета умножают на площадь одного квадрата.

Так, квадрату размером 2×2 мм на плане масштаба 1:1000 соответствует на местности квадрат 2×2 м, то есть площадь равная 4 м 2 . Если подсчитанное число квадратиков равно 122,4, то площадь участка равна 122,4 · 4 м 2 = 490 м 2 .

Рис. 5.1 Палетка с параллельными линиями

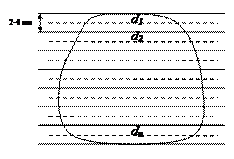Для измерения площади палеткой с параллельными линия­ми ее накладывают на план так, чтобы противоположные края участка расположились посредине между линиями палетки (рис. 5.1).

Отрезки линий палетки, ограниченные контуром участка, можно рассматривать как средние линии трапеций, заключенных на рисунке между пунктирными линиями. Из­мерив длины средних линий d₁, d₂, . d_n, площадь участка вычисляют по формуле (5.1):

где h — расстояние между линиями палетки (в масштабе).

Определение суммы отрезков d₁ + d₂ + … + d_n выполняют циркулем-измерителем. Взяв в раствор измерителя отрезок d₁, переносят измеритель на следующую линию, на продолжение отрезка d₂ и увеличивают раствор так, что в растворе будет набрана сумма d₁ + d₂. Продолжая, накапливают всю сумму расстояний и определяют ее значение по масштабной линейке.

Прямоугольная палетка построена в виде сетки квадратов. Определение площади прямоугольной палеткой выполняют по способу А.Н. Савича (рис.5.2).

Способ А. Н. Савича применяется при измерении на плане больших площадей. Часть Р₀ площади участка (рис. 5.2), состоящая из целых квадратов, образованных линиями координатной сетки, не требует измерения – она равна сумме известных площадей квадратов. Измеряют площади Р₁, Р₂, Р₃, Р₄, расположенные на краях участка и составленные

нецелыми частями квадратов. Вся измеряемая площадь равна

Рис. 5.2 Измерение площади способом Савича

Р = Р₀ + Р₁ + Р₂ + Р₃+ Р₄. (5.2)

Измерение площадей Р₁, Р₂, Р₃, Р₄ может быть выполнено любым из описанных выше методов (по координатам, по линейно-угловым измерениям).

Рис. 5.3 К способу Савича

Для повышения точности измерения площадей Р₁, Р₂, Р₃ и Р₄ рекомендуется измерять еще и дополнения этих площа­дей до целых квадратов и окончательные их значения вычис­лять. Пусть, например, непосредственное измерение площади Р₁ дало результат R (рис. 5.3). Измерением площади, дополняющей R до пяти целых квадратов, получен результат Q. Если бы не погрешности измерений и деформации бумаги, то сумма R + Q равнялась бы точно P_Q – площади прямоуголь­ника, состоящего из пяти квадратов. Полагая погрешности пропорциональными размерам измеряемых площадей, напишем пропорцию , откуда следует . (5.3)

Достоинством способа Савича является то, что значитель­ная часть площади (а именно – Р₀) определяется без измере­ний, аналитически. Уменьшение измеряемой части площади и выполнение измерений с контролем повышают точность оп­ределения площади. Кроме того, оказывается учтенной дефор­мация бумаги.

Если значительная часть площади составлена целыми квад­ратами, а измерять приходится лишь малую ее часть, точность способа Савича близка к точности аналитических способов.

5.2 Способы определения площади участка с криволинейными границами

Источник

Определение площади палетками

Для определения на плане площадей небольших участков с криволинейными контурами применяют прямолинейные и кри­волинейные палетки. К прямолинейным относят известные и наиболее распространенные квадратные и параллельные палетки.

Квадратная палетка представляет сеть взаимно перпендику­лярных линий, проведенных через 1 мм на прозрачном целлулои­де, плексигласе, фотопленке, стекле или восковке (рис.1.1, а). Площадь фигуры вычисляют простым подсчетом клеток палетки, наложенной на фигуру. Доли клеток, рассекаемых контуром на части, учитывают на глаз. Как видно на рисунке 5.2, а, площадь контура занимает 58 клеток 1 . Для плана масштаба 1:10 000 пло­щадь клетки со стороной 1 мм равна 10×10= 100 м 2 = 0,01 га. Сле­довательно, площадь контура равна 0,58 га.

Для упрощения подсчетов проводят утолщенные линии через 0,5 и 1 см, чтобы число клеток можно подсчитать сразу группами (25 и 100 мм 2 ).

Квадратной палеткой не рекомендуют определять площади, большие 2 см 2 на плане.

Недостаток ее применения помимо того, что площади долей клеток, рассекаемых контуром, приходится оценивать на глаз, со­стоит еще в том, что подсчет числа целых клеток нередко сопро­вождается грубыми ошибками.

Таких недостатков не наблюдается при определении площадей параллельной палеткой, представляющей собой листок прозрачно­го целлулоида, плексигласа или восковки, на котором нанесены параллельные линии, проведенные преимущественно через 2 мм одна от другой (рис.1.1, б).

Площадь контура этой палеткой вычисляют следующим обра­зом. Накладывают ее на контур так, чтобы крайние точки а и b разместились посередине между параллельными линиями палет­ки. Таким образом, весь контур оказывается расчлененным парал­лельными линиями на фигуры, близкие к трапециям с одинако­выми высотами, причем отрезки параллельных линий внутри кон­тура являются средними линиями трапеций. Прерывистыми ли­ниями на рисунке 1.1, б показаны основания этих трапеций. Сумма площадей трапеций, т. е. площадь контура,

P=cdh + efh + mnh + . + klh.

Так как все высоты трапеций равны,

.

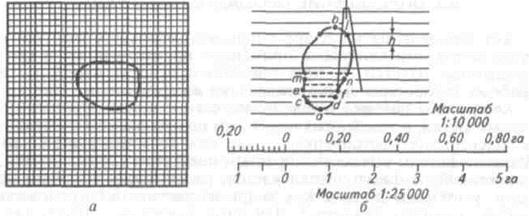Рис. 1.1 – Определение площади контура квадратной (а) и параллельной (б) палетками

Следовательно, чтобы получить площадь контура, нужно взять сумму средних линий, т. е. сумму отрезков параллельных прямых, проходящих внутри контура, и умножить на расстояние между ними.

Для упрощения определения площади сумму средних линий последовательно набирают в раствор циркуля: сначала берут отрезок cd, затем, не сжимая циркуля, совмещают левую его ножку с точкой /(см. рис. 5.2, б). После этого, не сдвигая правую ножку циркуля с места, увеличивают раствор циркуля, установив левую ножку в точку е. Таким образом, в растворе циркуля получают отрезок, равный cd + ef. Далее левую ножку циркуля устанавливают в точку л, вследствие чего пра­вая ножка встанет от точки п на расстоянии cd + ef После этого, не сдвигая пра­вую ножку с места, раствор циркуля увеличивают, установив левую ножку в точку т, и т.д. Последним отрезом, набираемым в раствор циркуля, будет отрезок к). Набранную в раствор циркуля сумму средних линий определяют по масштабной линейке, и полученную длину умножают на расстояние Л, соответствующее числу метров на местности.

Например, если масштаб плана 1:10 000, h – 20 м и сумма сред­них линий равна 682 м, то площадь контура будет равна 13 640 м 2 , или 1,36 га. Чтобы не выполнять подобных вычислений, для нуж­ного масштаба плана строят специальную шкалу, по которой от­считывают площадь контура, зная сумму средних линий. Рассчи­таем основание шкалы для масштаба 1:10 000. При расстоянии между параллельными линиями 2 мм и при основании шкалы 1 см площадь будет равна 20 • 100 = 2000 м 2 = 0,20 га. Следовательно, каждому сантиметру шкалы будет соответствовать 0,20 га на мест­ности. Левое основание шкалы делят на 10 частей, как это делают при построении линейного масштаба (см. рис. 1.1, б).

Основанию масштаба 1:25 000, равному 1 см, будет соответство­вать площадь 1,25 га. Такое основание неудобно для определения площадей, поэтому следует рассчитать основание, которому соот­ветствует площадь 1 га. В этом случае длина основания, очевидно, будет равна 0,8 см. Левое основание шкалы также делят на 10 час­тей.

Для масштаба 1:5000 основание принимают 2 см, которое будет соответствовать площади 0,1 га.

После того как сумма средних линий в раствор циркуля набра­на, определяют площадь по шкале так же, как расстояния по ли­нейному масштабу. Палетку и шкалу обычно строит сам исполни­тель. Параллельной палеткой не следует определять площади больше 10 см 2 на плане.

К криволинейным относят гиперболические палетки, представляющие систе­му гиперболических кривых и применяющиеся для определения площадей про­стейших геометрических фигур. Эти палетки не находят заметного распростране­ния, так как при помощи их нельзя быстро определить площадь участка с криво­линейным контуром.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Палетка. Измерение площади фигуры с помощью палетки

Урок 7. Математика 4 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Палетка. Измерение площади фигуры с помощью палетки»

Вы знаете, я хотела узнать площадь нашей страны, но мне это не сразу удалось сделать. Дело в том, что её границы имеют неправильную форму – это не прямоугольник, не квадрат, и даже не круг.

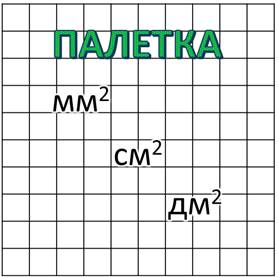
Я обратилась за помощью к нашей царице, и она рассказала мне, как находить площадь любой, самой искривлённой фигуры. Царица дала мне вот такое простое приспособление. Это прозрачная пластина или плёнка с разлиновкой в клеточку. Называется она – палетка. В зависимости от размера фигуры, площадь которой надо узнать, палетка может быть разделена на квадратные миллиметры, квадратные сантиметры или квадратные дециметры.

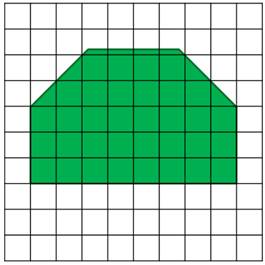
Представьте себе, что надо узнать площадь вот такой фигуры.

Накладываем на неё палетку.

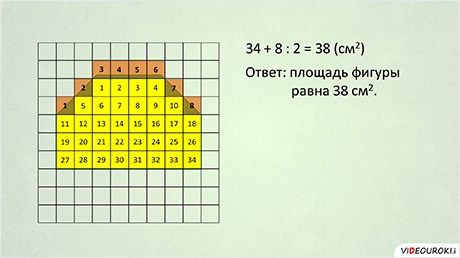
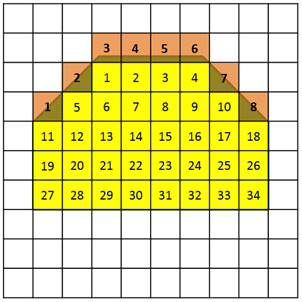
Сначала считаем, сколько всего целых квадратиков. Их тридцать четыре. Теперь считаем все оставшиеся кусочки. Их восемь. Люди договорились, что каждые два кусочка засчитывают за один полный квадратик. Поэтому количество кусочков делим на два. Получилось четыре.

Складываем тридцать четыре и четыре. Это тридцать восемь. Значит, площадь этой фигуры – примерно тридцать восемь квадратиков.

Так как в школе чаще всего пользуются палетками, разделёнными на квадратные сантиметры, то вы бы сказали, что площадь данной фигуры примерно равна тридцати восьми квадратным сантиметрам. Почему примерно? Потому что площадь фигуры по палетке вряд ли возможно определить абсолютно точно, ведь редко два кусочка могут идеально заменить целый квадратик.

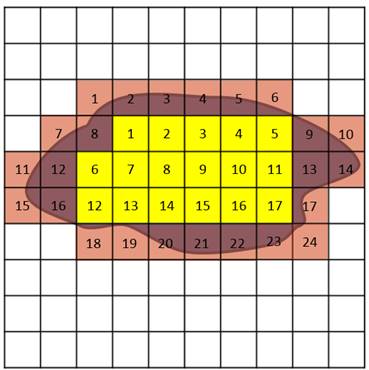
А теперь попробуем найти площадь вот такой, совершенно бесформенной фигуры.

Опять накладываем на неё палетку. Считаем целые квадратики.

Их семнадцать. Теперь считаем кусочки. Их двадцать четыре. Количество кусочков делим на два и полученное число прибавляем к семнадцати. Получилось примерно двадцать девять квадратных сантиметров.

Иногда случается и так, что количество кусочков – нечётное число, например, тринадцать или двадцать пять. Тогда делим на два ближайшее чётное число, больше данного на один. Ведь всё равно при помощи палетки точно площадь фигуры измерить невозможно. А вот почему берём чётное число больше данного, вы узнаете в пятом классе.

Запомнили, ребята, как мы определяем площадь фигур с помощью палетки?

̶ Накладываем палетку на фигуру.

̶ Считаем количество целых квадратов.

̶ Считаем количество кусочков.

̶ Количество кусочков делим на два…

̶ Складываем полученное число с количеством целых квадратов….

̶ Записываем ответ.

Видите, всё просто!

Кстати, именно так, используя план местности и палетку, можно найти площадь участка земли, или озера, или целого города, и даже страны. Вот этим я сейчас и займусь. Пока, ребята!

Источник