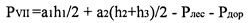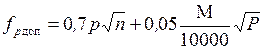Определение площади участков графическим способом



Графический способ определения площадей состоит в том, что участки, изображённые на плане, разбивают на треугольники, в которых высоты по величине близки к основаниям. Зная высоту и основание, вычисляют площадь.
Для контроля и повышения точности вычислений площадь каждого треугольника определяют дважды: по двум различным основаниям и высотам. Допустимость расхождения между двумя значениями площади определяют по формуле
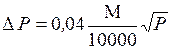
где М — знаменатель численного масштаба плана;
Р — площадь треугольника, га.
Для определения площадей небольших криволинейных участков применяют палетки.
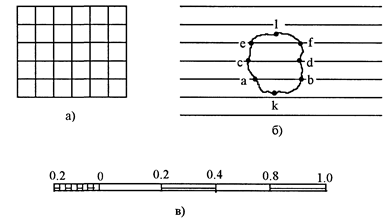
Квадратная палетка (рисунок 4а) — это сетка квадратов со сторонами 1-2 мм. Площадь участка определяется подсчётом квадратов палетки, наложенной на фигуру. Рекомендуется при определении площадей участков не более 2 см 2 на плане.
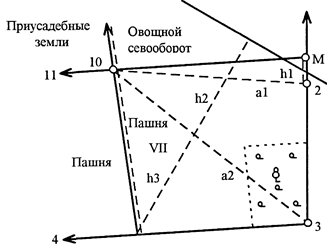
Параллельная палетка (рисунок 4б) — это ряд параллельных линий, проведённых на расстоянии 2 мм. Палетку накладывают на участок так, чтобы крайние её точки k и l были расположены между её линиями. Измерив, средние линии трапецией ab, cd, ef в масштабе плана и умножив их сумму на расстояние между линиями палетки, получают площадь участка. Рекомендуется при определении площадей до 10 см 2 на плане.
Чтобы не выполнять вычислений строят специальную шкалу — масштабную палетку (рисунок 4в), по которой определяют площадь участка, зная сумму средних линий. Рассчитаем основание шкалы для масштаба 1:10000. При расстоянии между параллельными линиями 2 мм и при длине шкалы 1 см площадь будет равна 20 ´ 100 = 2000 м 2 = 0,20 га. Следовательно, каждому сантиметру шкалы будет соответствовать 0,20 га на местности. Левое основание шкалы делят на 10 частей. После того как сумма средних линий набрана в раствор циркуля, определяют площадь по шкале так же, как расстояние по линейному масштабу.
Точность однократного определения площадей квадратной и параллельной палетками в среднем характеризуется формулой
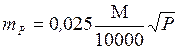
где М — знаменатель численного масштаба плана;
Р — площадь фигуры, га.
2.2.1 В соответствии с рисунком 5 определить графическим способом площадь пашни восточной части поля VII.
Площадь пашни восточной части поля VII вычислить по формуле
2.2.2 Построить параллельную и масштабную палетки для масштаба плана и, пользуясь ими, определить площади прудов в северной и южной части землепользования.
2.3 Определение площадей участков механическим способом
2.3.1. Определение цены деления планиметра
Выполнив поверку основного геометрического условия планиметра, определяем цену деления планиметра путем обвода двух квадратов координатной сетки, по два обвода при каждом положения полюса. Цену деления планиметра определяем по формуле
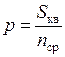
где S — площадь квадратов координатной сетки;
n ср — среднее значение разности отсчетов.
Цену деления p выражают четырьмя-пятью значащими цифрами в зависимости от величины первой цифры
2.3.2. Составление кальки контуров
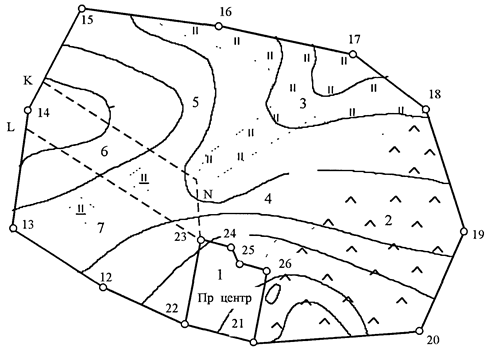
Разделить массив пашни в северной части землепользования на участки в соответствии с рисунком 6, при этом границы между ними провести карандашом (линии NK и 23 — L параллельны линии 13 — 12), обозначить номера контуров. Вкрапленные контуры обозначить тем же номером, что и основной контур с добавлением индекса “а”, “б” и т.д.
2.3.3. Определение площадей контуров планиметром.
Определить площадь каждого контура двумя обводами планиметра при одном положении счётного механизма.
Площади вкрапленных контуров определить планиметром способом повторений (3-4 повторения), снимая отчеты перед первым обводом и после последнего; разность отчётов разделить на число обводов.
Площади участков угодий вычислить по среднему значению цены деления планиметра , округляя значения площадей до 0.01 га.
Невязку определить по формуле fp = å Рвыч — Ртеор и сравнить её с допустимой
где р — цена деления планиметра;
n — число контуров, площади которых определяют планиметром;
М — знаменатель численного масштаба плана;
Р — общая площадь участка.
Если невязка допустима, распределить её с обратным знаком пропорционально площадям угодий.

Результаты вычислений сводим в таблицу 2.
Таблица 2 — Ведомость вычисления площадей планиметром
Источник
Определение площади полигона



Для определения площади строительных участков применяют следующие способы: графический, аналитический, механический.
В выполняемой работе использовать аналитический способ.
Площадь полигона можно вычислить по координатам его вершин. Исходными данными являются координаты точек (вершин) теодолитного хода (полигона).
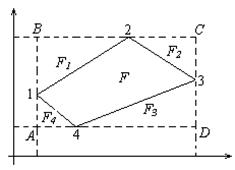
Рис. 3.4.1 — Схема проекций точек теодолитного хода на координатные оси
Рис. 3.4.2 — Схема определения площади полигона аналитическим способом
— замкнутый полигон 1-2-3-4-1, (1-2-3-4-5-6-1);
Определить: площадь F полигона.
 , , | (3.4.1) |
где 

Подставим значение площадей в исходную формулу, раскроем скобки и после приведения подобных членов получим:
 . . | (3.4.2) |
Вынесем за скобки одноименные значения:
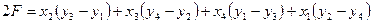 . . | (3.4.3) |
То есть удвоенная площадь полигона равна сумме произведений (для каждой точки полигона) абсциссы х на разность между ординатами у последующей и предыдущей точек.
Данный полигон состоит из четырех точек, поэтому в формуле получилось четыре таких слагаемых. Для полигона из n точек формула примет вид:
 . . | (3.4.4) |
Формулу 7.5 следует читать так: двойная площадь полигона (многоугольника) равна сумме произведений абсциссы каждой точки на разность ординат последующей и предыдущей точек.
Формула для вычисления площади полигона: в формуле (7.4) за скобки можно вынести у:
 , , | (3.4.5) |
После преобразования формула будет иметь вид:
 . . | (3.4.6) |
Формулу 7.7 следует читать так: двойная площадь полигона (многоугольника) равна сумме произведений ординаты каждой точки на разность абсцисс предыдущей и последующей точек теодолитного хода.
Вопросы для контроля:
1. Какой порядок камеральных работ при построении плана теодолитной съемки?
2. Перечислите способы съемки ситуации.
3. По какой формуле вычисляют площадь полигона, контроль?
4. Как контролируют правильность нанесения точек теодолитного хода?
5. Какой размер пересечения координатных линий, каким цветом рисуют?
Источник
Определение площадей земельных участков
1. ПРИЁМЫ И ТОЧНОСТЬ ВЫЧИСЛЕНИЯ ПЛОЩАДЕЙ ЗЕМЛЕПОЛЬЗОВАНИЙ И КОНТУРОВ УГОДИЙ
На практике землеустроительных работ применяют различные способы определения площадей. Применение того или иного способа зависит от хозяйственного значения участков, их размеров и форм (конфигурации и вытянутости), наличия или отсутствия результатов измерений линий и углов на местности и планово-картографического материала требуемой точности при решении инженерно-технических и планово-экономических задач.
Известны аналитический, графический и механический способы определения площадей. Нередко применяют сочетания этих способов, то есть их используют комбинированно.
Аналитический метод предполагает вычисление площадей землепользовании по результатам полевых линейных и угловых измерений или по их функциям — координатам вершин полигонов.
Графический метод применяют при отсутствии полевых результатов измерений, площади вычисляют по результатам измерений линий и углов на плане или по графическим координатам.
Механический метод представляет собой определение площадей на плане при помощи специальных приборов (планиметров и др.).
Наиболее точным считается аналитический метод, при котором площади вычисляют по результатам измерений на местности линий и углов или по координатам вершин полигонов на ЭВМ. Точность аналитического способа зависит только от качества полевых измерений. При измерении площади по топографической основе графическим и механическим методами на точность определения площади дополнительно влияют качество графического построения участка, масштаб карты или плана, деформация бумаги, погрешности приборов и другие факторы, снижающие точность этих способов.
2. Вычисление площадей полигонов (контуров участков)
графическим способом
Сущность вычисления площадей графическим способом заключается в том, что изображенный на плане участок или землепользование делят на простейшие геометрические фигуры: чаще всего треугольники, реже прямоугольники и трапеции; в каждой фигуре измеряют на плане ее элементы — высоты, основания средние линии, по которым вычисляют площадь. Сумма площадей фигур дает площадь участка.
Графический способ удобно применять тогда, когда граница участка представляет собой ломаную линию с небольшим числом поворотов. Чем больше углов имеет граница участка, тем меньше эффективность этого способа. Поэтому для вычисления площадей участков, имеющих большое количество углов, целесообразнее вычислять площадь по графическим координатам точек, то есть по координатам, измеренным на плане.
Иногда при делении участка на геометрические фигуры измеряют на плане не высоты и основания, а линии и углы этих фигур. Для вычисления площадей применяются те же формулы, что и в аналитическом способе, площадь треугольника по высоте и основанию вычисляется по формуле:
где а -основание, h — высота.
Площадь прямоугольника вычисляется по формуле:
где а и Ь — стороны прямоугольника.
Площадь трапеции вычисляется по формуле:
где h- высота, а и Ь — основания,
или P=hl, где l=(a+b)/ 2 — средняя линия, h — высота.
Наилучшим вариантом разбивки участка на треугольники будет тот, при котором треугольники близки к равносторонним. То есть высоты по величине близки к основаниям.
При реализации графического способа на точность вычисления площади помимо погрешностей измерений на местности влияют погрешности составления плана, погрешности измерений на плане, деформация бумаги. Относительная погрешность определения площади графическим способом составляет 1/500 -1/1000.
Графический способ применяют для определения площадей землепользовании, полей севооборотов, контуров угодий, ограниченных ломаными линиями, при этом, чем меньше площадь участка, тем с большей относительной погрешностью определяется его площадь, а для больших площадей, например, целых землепользовании, точность этого способа приближается к точности аналитического метода.
Часто для повышения точности определения площадей длины линий (сторон и оснований) по плану не измеряют, а принимают величины, полученные измерением на местности, если таковые имеются. Точность вычисления площади неравностороннего треугольника будет выше в том случае, если короткое основание (или высота) измерено на местности, а длинная высота (основание) определена по плану. Результаты измерений на местности следует использовать максимально.
Для контроля и повышения точности вычисления площадь каждого треугольника определяют дважды: по двум различным основаниям и высотам. Если расхождение между двумя значениями допустимо, то из этих значений площади вычисляют среднее.
3. Определение площадей участков (контуров полигонов)
механическим способом
Механический способ подразумевает определение площадей по плану (карте) при помощи специальных приборов — планиметров. Механический способ является наименее точным, но наиболее распространенным, так, как пользуясь им, можно быстро и просто определить площадь участка любой формы, поэтому его применяют при определении площадей землепользовании, полей севооборотов, контуров угодий с извилистой формой границ, проходящих по живым урочищам, горизонталям, бровкам лощин, очертаниям болот, зарослей и т.д.
Механический способ определения площадей состоит в обводе фигуры любой формы на плане планиметром. Механический способ менее точен, чем аналитический и графический, так как на погрешности влияют, кроме погрешностей измерений на местности и составления плана, погрешности измеряемых приборов. Точность определения площадей этим способом характеризуется относительной погрешностью 1/200 — 1/400.
Планиметр — геодезический механический прибор, предназначенный для определения площади путем обвода фигуры любой формы на плане. Существуют планиметры самых разнообразных систем. Планиметры делятся на линейные и полярные.
К линейным относятся планиметры, у которых во время обвода фигуры все точки прибора подвижны, например, простейший планиметр-топорик.
Наиболее распространены полярные планиметры, состоящие из двух рычагов — обводного и полюсного, соединенных шарниром в одной точке. Обвод фигуры производится обводным индексом, расположенным на конце обводного рычага. Во время обвода одна точка планиметра, расположенная на конце полюсного рычага, всегда остается неподвижной. Эта точка называется полюсом. Полюс закрепляется на плане с помощью иглы или груза.
Полярные планиметры бывают простые и компенсационные. Различают также планиметры с постоянным и переменным обводным рычагом.
Результат обвода фигуры (измерения площади) определяется вращением счетного ролика, который при обводе фигуры соприкасается с поверхностью бумаги. Счетный ролик является самой ответственной частью планиметра. Для его фрикционного сцепления с бумагой на ободке счетного ролика нанесены рифельные штрихи. На цилиндрической поверхности счетного ролика имеются деления, по которым отсчитывают результаты обводов.
Фигуру площадью до 400 см2 на плане обычно обводят с положением полюса вне фигуры, при этом угол, образованный рычагами планиметра, во время обвода должен быть не менее 30° и не более 150°, а в начале обвода угол между рычагами планиметра должен быть близок к прямому (90°).
Каждому делению планиметра соответствует на плане или на местности площадь р, называемая ценой деления планиметра.
Цену деления p выражают четырьмя-пятью значащими цифрами в зависимости от величины первой цифры.
Тогда площадь обведенной фигуры определится по формуле: Р=Uр, где U – отсчёт по шкале планиметра. Эта формула показывает, что для вычисления площадей обводимых фигур необходимо знать величину р — цену деления планиметра, которая представляет площадь, соответствующую одному делению планиметра. Точность определения площади полярным планиметром зависит главным образом от размеров обводимых фигур. Чем меньше площадь, тем больше относительная погрешность ее определения.
4. Аналитический способ подсчета площадей участков
Этот способ предполагает использование формул геометрии и тригонометрии при расчете площадей участков. Использование его наиболее целесообразно при наличии результатов непосредственных измерений на местности углов и линий или их функций — приращений координат, а так же координат вершин полигона.
Уже само по себе использование непосредственно измеренных величин обеспечивает аналитическому способу возможности достижения наиболее высокой точности среди всех известных способов.
5. Точность определения площади земельного участка
Учитывая то, что точность определения земельного участка непосредственным образом влияет на размер выплат в виде земельного налога государству, либо арендодателю в виде арендной платы. Рассмотрение данного вопроса является неотъемлемой частью данного пункта работы.
В соответствии с Инструкцией по межеванию земельных участков опубликованной Комитетом Российской Федерации по земельным ресурсам и землеустройству в 1996 году, отметим основные положения, касающиеся точности определения площади и границ земельных участков [7].
1. Межевание земель выполняют как в общегосударственной, так и в местных и условных системах координат. При этом должна быть обеспечена надёжная связь местных и условных систем координат с общегосударственной системой.
2. Геодезической основой межевания земель служат:
— пункты ГГС (триангуляция и полигонометрия);
— пункты ОМС (опорные межевые знаки — ОМЗ).
3. Пункты ОМС (ОМЗ) служат в качестве исходных для
— закрепления на местности выбранной местной или условной системы координат и последующей её привязки к общегосударственной системе координат;
— оперативного восстановления утраченных межевых знаков;
— решения других задач государственного земельного кадастра и землеустройства.
6. Вынос в натуру и определение границ землепользования
Определение границ землепользования является основной и главной задачей проведения инвентаризации земельных участков, поэтому проведению работ связанных с определением, восстановлением и выносом границ земельных участков уделяется повышенное внимание.
Геодезические работы по выносу в натуру границ землепользования выполняют аналогично разбивочным работам по выносу в натуру заданий, сооружений и других объектов жизнедеятельности человека.
Базовой основой геодезических работ является проект. При землеустроительных работах основными объектами проектирования являются границы районов, городов, посёлков городского типа, сельских населённых пунктов, границы отдельных землевладений, приусадебных, садово-огородных, дачных, арендных и других земельных участков, имеющих статус самостоятельных территориальных образований.
В зависимости от административных решений, хозяйственной ценности и занимаемой площади объектов землеустройства проектирование границ ведётся на основе геодезических измерений на местности или с использованием топографических материалов различного вида и масштабов, включая и цифровые модели (электронные карты). По данным землеустроительного проекта выполняют геодезическое проектирование. Оно включает в себя аналитическую подготовку данных для перенесения на местность проектных точек наиболее целесообразными способами, обеспечивающими требуемую точность их положения, и составление разбивочных чертежей.
При аналитической подготовке координаты выносимых в натуру точек вычисляют в государственной или местной системе координат. При необходимости перевычисляют координаты из местной системы, в государственную и наоборот. Однако во всех случаях координаты выносимых точек должны вычисляться в той же системе, что и координаты пунктов исходного геодезического обоснования.
Исходным геодезическим обоснованием могут служить все виды геодезических построений, обеспечивающие требуемую точность выноса в натуру границ землепользования: триангуляция, трилатерация, линейно-угловые сети, полигонометрия, спутниковые определения и в ряде случаев теодолитные ходы.
Вынос в натуру точек границ землепользования от пунктов исходного обоснования производят всеми известными способами разбивочных работ: угловыми, линейными, створными и створно-линейными засечками; способами полярных и прямоугольных координат, перпендикуляров, теодолитными ходами и другими геодезическими построениями.
Вынесенные в натуру точки, как правило, закрепляют специальными межевыми знаками. Ими могут служить также чётко опознаваемые контурные точки, такие как углы капитальных заборов или зданий на застроенной территории, пересечения осей дорог, угловые точки угодий, урочищ и другие бесспорно опознаваемые точки местности. В этом случае путём соответствующих геодезических измерений определяют координаты этих точек.
Полученные данные переносят на кадастровые планы и заносят в кадастровый банк данных. В случае необходимости, например, при выдаче акта на владение землей, составляют чертёж границ земельного участка.
От точности геодезических данных зависит достоверность кадастровой информации. Поскольку во всех операциях с землёй (установлении прав собственности, купле-продаже, дарении, сдаче в аренду и другие) обязательно фигурирует площадь земельного владения, то требуемая точность её определения служит расчётной основой для назначения точности выноса в натуру и определения границ землепользования.
В практике геодезических работ для земельного кадастра принято считать, что для городских земельных участков площадью до 1 гектара координаты точек их границ следует определять со средней квадратической ошибкой 2 сантиметра, для участков значительной площади — 5 — 10 сантиметров.
Источник