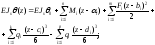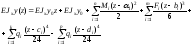Определение перемещений при изгибе способы решения интегралов

Вопрос 18.Определение перемещений при изгибе. Интеграл Мора. Метод Верещагина.

Прогиб – линейная деформация, смещение центра тяжести поперечного сечения.

Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление.

— перемещение сечения К под действием Р, где M_xp-изгибающий момент в произвольном сечении, _х— единичный момент в том же сечении под действием единичной силы или единичного момента ( если ищется угол поворота), EI_x– жёсткость сечения балки при изгибе.

Правило Верещагина. Используется, когда жёсткость при изгибе постоянна вдоль длины. Эпюра изгибающих моментов должна быть линейной. Максимальный прогиб называется стрелой.

Следует иметь в виду, что способы «перемножения» эпюр применимы только при наличии двух условий:

1.Изгибная жесткость балки на рассматриваемом участке должна быть постоянной(EI=Const),

2.Одна из двух эпюр моментов на этом участке (грузовая или единичная) должна быть обязательно линейной. При этом обе эпюры не должны в пределах данного участка иметь перелома.

Δ_кр= 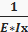* ω_p * _k c — грузовое перемещение

ω_p– площадь грузовой эпюры.

_k c — ордината в единичном эпюре, соответствует центру тяжести грузовой.

При постоянной жесткости по длине балки EI_z для определения прогиба энергетическим методом необходимо вычислять интеграл вида:

.

Допустим, что эпюры изгибающих моментов аналитически выражаются функциями М_z=f₁(х), М ’ _z´ = f₂(х), причем одна из них, например, f₁(х) произвольная, а другая f₂(х) линейная функция и может быть записана в виде f₂(х) = kх+b. Пусть графики этих функций имеют вид представленный на рис. 3.86.

В соответствии с принятыми обозначениями можно записать:

Первый интеграл представляет собой статический момент относительно оси x площади эпюры ограниченной кривой M_z, т.е.

, где

ω – площадь, ограниченная кривой M_z,

х_c — координата центра тяжести фигуры ограниченной кривой M_z относительно оси х.

Второй интеграл представляет собой площадь, ограниченную кривой M_z, которую обозначили ω.

Таким образом, искомый интеграл равен произведению площади эпюры M_z на расположенную под ее центром тяжести ординату эпюры М_z´. Важно отметить, что вычисление перемещения способом Верещагина возможно только в том случае, когда, во-первых, эпюры M_z и М_z´ на рассматриваемом участке не имеют изломов, во-вторых, одна из эпюр описывается линейной зависимостью и именно по ней определяется ордината под центром тяжести другой эпюры y_c. Поэтому при вычислении способом Верещагина интеграл Мора по всей длине балки надо заменить суммой интегралов по участкам, в пределах которых эпюра моментов от единичной нагрузки не имеет изломов. Тогда перемещение сечения балки δ:

Таким образом, для вычисления прогибов по способу Верещагина необходимо:

1) построить эпюру изгибающих моментов от заданных нагрузок M_z (основная эпюра);

2) снять внешнюю нагрузку (но сохранить опоры) и приложить в том сечении, в котором определяется перемещение (угол поворота) единичную силу (единичный момент) в направлении искомого .перемещения (угла поворота);

3) построить эпюру изгибающих моментов от единичной нагрузки М_z´(единичная эпюра);

4) разбить эпюры на участки, в пределах которых отсутствуют изломы эпюр, и для каждого участка вычислить площадь криволинейной эпюры ω_i и ординаты эпюр ограниченных линейной функцией под центрами тяжести криволинейных эпюр у_ci.

5) составить произведения ω_i у_ci и просуммировать:

Встречающиеся на практике эпюры изгибающих моментов разбивают на простейшие фигуры: прямоугольник, треугольник и параболический треугольник.

Площади этих фигур и координаты центров тяжести приведены в таблице

Источник

9.10. Способы определения перемещений при изгибе

Метод непосредственного интегрирования дифференциального уравнения упругой линии балки.

Уравнение дает возможность вычислить линейные и угловые перемещения сечений. Первое интегрирование дифференциального уравнения определяет закон изменения углов поворота сечений по длине балки:

.

Второе интегрирование полученного выражения позволяет определить функции прогибов точек упругой линии по длине балки:

.

При вычислении интегралов сначала составляем аналитические выражения изгибающего момента и жесткости в зависимости от координаты сечения z, в котором определяются перемещения. Постоянные интегрирования С и D находятся из граничных условий, которые зависят от способов закрепления балки. Для однопролетной балки прогибы над опорами равны нулю. Для защемленной в опорном сечении балки прогиб и угол поворота равны нулю.

Рассмотрим пример. Найти перемещения консоли постоянного сечения, загруженной на свободном конце силой F (рис. 9.23).

Рис. 9.23. Схема консольной балки, загруженной на свободном конце

В заделке возникает вертикальная реакция R_A = F и изгибающий момент М_A = Fl. Начало координат поместим на левом конце балки. Изгибающий момент в произвольном сечении, расположенном на расстоянии z от начала координат, определяется по формуле

далее с учетом уравнения упругой линии имеем:

.

Если жесткость балки – величина постоянная, то интегрируя уравнение упругой линии, получим:

;

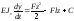
Для нахождения постоянных интегрирования С и D используем граничные условия.

При z = 0 (левый конец балки – заделка) угол поворота и прогиб равны нулю, тогда

Подставляя эти значения в интегралы, находим, что С = D = 0, тогда

;

.

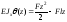
Определим максимальные значения перемещений:

;

.

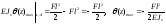
Знак «минус» в формуле угла поворота свидетельствует о том, что поворот сечения происходит по часовой стрелке, знак «минус» в формуле прогиба указывает на то, что прогиб происходит вниз (не совпадает с положительным направлением оси у).

Если балка по условиям нагружения разбивается на п участков, то из условий непрерывности и плавности упругой линии необходимо составить и решить систему 2п уравнений. Совместное решение системы уравнений позволит найти постоянные интегрирования и получить для каждого участка уравнения прогибов и углов поворота. Необходимость совместного решения системы уравнений осложняет задачу, поэтому непосредственное интегрирование применяют только в тех случаях, когда число участков невелико (один, максимум два).

Метод начальных параметров.

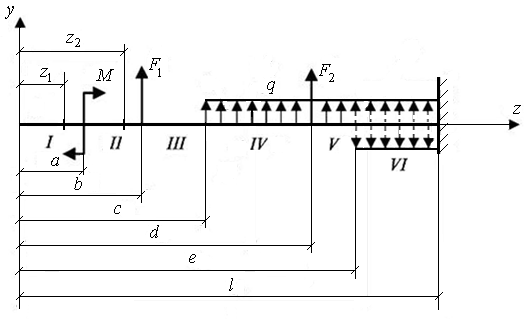
Рассмотрим балку постоянной жесткости, загруженную положительными сосредоточенными моментами, силами и равномерно распределенной нагрузкой. Они считаются положительными, если вызывают в сечении положительный изгибающий момент (рис. 9.24).

Начало координат возьмем на левом конце балки, ось z направим вправо, ось у – вверх. Разобьем балку на ряд участков.

Рис. 9.24. Схема к расчету балки методом начальных параметров

,

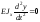
проинтегрируем уравнение упругой линии, получим:

; EJ_xy(z) = C₁z + D₁.

Умножим изгибающий момент на величину (z₂ – a) 0 , равную единице:

,

после интегрирования имеем:

.

Постоянные интегрирования определим из условия, что упругая линия не имеет разрывов и изломов и является плавной кривой. На границе первого и второго участков имеем:

,

,

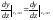
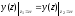
Определим физический смысл постоянных интегрирования С и D. Если обозначить угол поворота и прогиб в начале координат через θ₀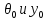 и у₀, то из уравнения упругой линии получим:

Рассмотрим последний шестой участок балки. Уравнение моментов в общем виде на этом участке имеет вид

.

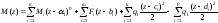
Проинтегрируем дважды это уравнение, получим:

При использовании полученных уравнений должны выполняться приведенные ниже требования.

При определении прогиба и угла поворота произвольного сечения в уравнения записываются слагаемые только для тех нагрузок, которые расположены между началом координат и рассматриваемым сечением. Если нагрузка относительно рассматриваемого сечения создает положительный изгибающий момент, то она входит в эти уравнения со знаком «плюс».

Распределенная нагрузка не должна прерываться. Если по условию задачи распределенная нагрузка оканчивается на одном из участков (конец пятого участка), то ее следует продолжить до конца балки, добавив одновременно нагрузку (добавленная и компенсирующая нагрузки показаны на расчетной схеме пунктиром, рис. 9.24) такой же интенсивности, но с противоположным знаком.

Если начало координат расположено на левом конце балки, то положительным будет угол поворота сечения против часовой стрелки. Если же начало координат взято на правом конце балки, то положительным будет угол поворота сечения по часовой стрелке. Линейное перемещение вверх будет положительным независимо от того, где расположено начало координат.

Жесткость балки должна быть постоянной на всех участках.

Начало координат является единым для всех участков балки.

Ось балки является прямолинейной.

Значения начальных параметров находятся из граничных условий в опорных сечениях балки. Если начало координат взято в жестко закрепленном опорном сечении, то начальные параметры будут равны нулю, т. е. θ₀ = 0 и у₀ = 0. Поэтому для консольной балки, имеющей жесткую заделку, начало координат обязательно следует размещать в этом сечении.

Если начало координат находится в сечении на шарнирной опоре, то θ₀ ≠ 0 и у₀ = 0.

Если же концевые сечения балки не являются опорными сечениями, то начальные параметры не равны нулю и их необходимо определять.

Для этого в общем виде находят прогибы в опорных сечениях и, приравняв их к нулю, получают уравнения для определения начальных параметров.

Определение перемещений и углов поворота различных сечений балки, лежащей на двух опорах, методом начальных параметров представляет собой достаточно трудоемкий процесс. Он требует громоздких вычислений по определению постоянных, интегрирования и граничных условий задачи.

Рассмотрим общий метод определения перемещений, пригодный для любой линейно деформируемой системы при любой нагрузке. Этот метод был предложен немецким ученым О. Мором.

Пусть требуется определить вертикальное перемещение у_c точки С балки, изображенной на рис. 9.25, а.

Источник