Модуль 1. «Биомеханические основы двигательного аппарата и двигательных действий» (стр. 7 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
В условиях действия гравитационного поля ОЦМ совпадает с общим центром тяжести (ОЦТ) и не совпадает в невесомости и водной среде. Общим центром тяжести называется воображаемая точка равнодействующей сил тяжести всех частей тела. Для тела, находящегося в космическом пространстве, где силы гравитационного притяжения отсутствуют, понятие центра тяжести бессмысленно.
В водной и воздушной среде для определения состояния равновесия тела необходимо знать положение центра объема (ЦО) и центра поверхности (ЦП) тела человека.
Центр объема тела – это точка приложения равнодействующей силы гидростатического давления, которая расположена на 2-6 см выше ОЦМ. Поскольку плотность тела неодинаковая, во время глубокого вдоха центр объема смещается вверх к поверхности головного отдела.
Центр поверхности тела – это точка приложения равнодействующей сил действия среды. Положение центра поверхности зависит от позы человека и направления потока среды, При высоких скоростях движения (например, прыжки), когда действует, достаточна большая сила сопротивления среды, от взаимного расположения общего центра масс и центра поверхности зависит сохранение положения равновесия тела человека или спортивного снаряда.
При изменении конфигурации (позы) тела человека изменяется положение центра масс звеньев тела, что обуславливает и изменение положения ОЦМ. Следовательно, положение ОЦМ тела определяется тем, где находится ЦМ отдельных звеньев тела. Для решения практических задач считают, что ЦМ звеньев тела расположены на их продольных осях, соединяющих центры соответствующих суставов (например, плечо, предплечье, бедро и т. д.). Если бы звенья тела были бы однородными по своему составу и плотности, а также имели форму правильных цилиндров, то ЦМ каждого из них находился бы на продольной оси звена и делил это звено на два равных участка. Однако звенья тела человека по своей форме похожи на усеченный конус, проксимальная часть которых тяжелее, поэтому ЦМ звеньев тела находится на продольной оси звена ближе к проксимальному концу. Вследствие этого ЦМ делит звено на две части таким образом, что проксимальная часть меньше половины длины звена, а дистальная часть больше.
Если рассматривать скелет как совокупность отдельных звеньев, соединенных в один организм, то окажется, что все эти звенья при нормальной стойке образуют систему, находящуюся в крайне неустойчивом равновесии. Так, опора туловища представлена шаровыми поверхностями тазобедренного сочленения. Центр масс туловища расположен выше опоры, что при шаровой опоре создает неустойчивое равновесие. То же самое относится и к коленному соединению и к голеностопному. Все эти звенья находятся в состоянии неустойчивого равновесия.
Центр масс тела человека расположен при нормальной стойке как раз на одной вертикали с центром тазобедренного, коленного и голеностопного сочленения ноги на 2 – 2,5 см ниже мыса крестца и на 4 – 5 см выше тазобедренной оси. У мужчин, в среднем, на 1-2 % выше, чем у женщин. В первые годы жизни у ребенка относительная высота общего центра масс значительно выше, чем у взрослых, в среднем на 10 – 15 %. Высокое расположение ОЦМ характерно для детей дошкольников (большая голова, маленькое тельце ребенка), что наряду со слабым развитием мышц туловища и конечностей обуславливает неустойчивое положение тела. К 5-6 годам высота ОЦМ достигает величин, сравниваемых с высотой положения ОЦМ у взрослых людей. В последующие годы, вплоть до старческого возраста, положение центра общего центра масс остается неизменным и, только возрастная инволюция приводит к смещению его положения. У спортсменов со значительной гипертрофией мышц нижних конечностей (штангисты, футболисты, бегуны) положение ОЦМ находится ниже, чем у людей, не занимающихся спортом. Существенное значение на положение
общего центра масс оказывают конституционные особенности. Существуют различные способы определения координат ОЦМ и ЦМ звеньев тела:
1) экспериментальный; 2) аналитический; 3) графический.
Одним из наиболее простых, экспериментальных методов исследования является метод взвешивания человека в избранной позе на специальной платформе, имеющей три точки опоры, одна из которых находится на неподвижном основании, а две другие находятся на весах. По показаниям весов без человека, F1 и F2 указывают величину давления на весы самой платформы. Взвесив человека, вновь определяют показания на весах F3 и F4 . Рассматривая по очереди две линии, соединяющие три точки опоры (равносторонний треугольник с вершиной на неподвижной основе) как оси вращения, можно написать уравнение моментов сил для системы, находящейся в равновесии:
Х = ____________ * h; У = _________ * h,
где Х и У – координаты ОЦМ, Р – вес тела, h – высота
В другом случае, для определения проекции ОЦМ человека на горизонтальную плоскость, также используют платформу в виде равностороннего треугольника, укрепленной на трех динамометрах, которые установлены на вершинах платформы.
В биомеханике наряду с экспериментальными методами используются и аналитические способы определения координат ОЦМ тела человека в фиксированной позе. Аналитические методы базируются на использовании статистических данных о геометрии масс тела человека, которые могут быть представлены в таблицах. Эти таблицы характеризуют связь веса отдельных сегментов тела человека с его общим весом и связь расстояния от проксимального конца сегмента до его центра масс с общей длиной сегмента. Геометрия масс тела (распределение масс тела) характеризуется такими показателями как: вес (масса) отдельных звеньев тела, положение центров масс отдельных звеньев и всего тела, моменты инерции и т. д. Расчетные методы позволяют повысить точность определения индивидуальных биомеханических параметров тела человека.
Кроме того, данные могут быть представлены в виде регрессионных уравнений, связывающих массы отдельных звеньев тела с антропометрическими признаками (общим весом, длиной тела и т. д.), либо с координатами их ЦМ.
Аналитический способ нахождения координат ЦМ звеньев тела, в основе которого лежит теорема Вариньона, широко применяется при изучении статических положений тела, системы тел и при изучении локомоторных движений:
Сумма моментов составляющих сил относительно оси равна моменту равнодействующей силы относительно той же самой оси.
Чтобы определить ЦМ звеньев тела необходимо рассмотреть моменты сил, создаваемые силами тяжести этих звеньев относительно оси координат. Например, момент силы тяжести плеча относительно оси У будет равен его весу (Рп), умноженному на плечо силы хЦМп
Мп (у) = Рп * хЦМп (1)
Аналогично определяется момент сил, создаваемый весом плеча относительно оси Х:
Мп (х) = Рп * уЦМп (2)
Для предплечья и кисти моменты силы тяжести относительно осей абсцисс и ординат будут следующими:
Мпр(у) = Рпр * хЦМпр
Мпр(х) = Рпр * уЦМпр
Согласно теореме Вариньона
ХОЦМ (Рп + Рпр + Рк) = хЦМп *Рп + хЦМпр * Рпр + хЦМк * Рк,
хЦМп * Рп + хЦМпр * Рпр + хЦМк * Рк
ХОЦМ = _____________________________________________ (3)
В данной формуле выражение ХЦМ * Р есть не что иное, как момент силы создаваемый силой тяжести соответствующих звеньев тела, относительно оси ординат (у). Следовательно, выражение (3) можно представить следующим образом:
Мп (у) + Мпр (у) + Мк (у)
Хоцм = _________________________________ (4)
Аналогичным образом определяется УОЦМ
УОЦМ (Рп + Рпр + Рк) = уЦМп * Рп + уЦМпр * Рпр + уЦМк *Рк,
уЦМп * Рп + уЦМпр * Рпр + уЦМк * Рк
Мп (х) + Мпр (х) + Мк (х)
УОЦМ = ________________________________ (5)
Используя формулы 4 и 5 можно определить положение общего центра масс, в нашем случае, руки при выполнении любого двигательного действия.
Уравнение множественной регрессии, с помощью которого можно наиболее точно оценить абсолютное положение ОЦМ у мужчин имеет вид:
У = 11,066 + 0,675 х1 – 0,173 х2 – 0,299 х3, где у – высота Положение ЦМ от подошвенной поверхности стопы (см), х1
– длина тела, х2 – обхват голени, х3 – длина корпуса.
Для вычисления относительного положения ОЦМ было определено уравнение множественной регрессии, в котором аргументами являются отношение массы туловища к массе тела (х1) и отношение среднегрудинного, переднезаднего диаметра к тазобедренному (х2). Уравнение регрессии имеет вид:
Для определения высоты положения общего центра масс у женщин спортсменок используют уравнение множественной регрессии вида:
У = — 4,667 + 0.289 х1 + 0,383 х2 + 0,301 х3.
Это уравнение включает следующие антропометрические показатели: х1 – длина ноги, см; х2 –длина тела в положении лежа, см; х3 – ширина таза, см.
Уравнение множественной регрессии для определения длины тела в положении лежа имеет вид:
У = — 7,445 + 1,059 х (см), где х – длина тела в положении стоя (см).
Между длиной тела в положении стоя и лежа существует разница. и др. (1973), применив методику с наклоном доски, установили, что такая разница составляет 4% от длины тела. Другие исследователи (Page,1974) считают, что изменение высоты ОЦМ при изменении позы (лежа или стоя) не превышает 1%. В положении лежа длина тела человека увеличивается, что обусловлено, как считают исследователи, снижением действия силы тяжести на позвоночный столб, перераспределением жидких сред в организме, смещением положения внутренних органов и снижением натяжения эпидермиса.
При биомеханическом анализе движений допускают, что положения центров масс звеньев конечностей являются постоянными. Такое предположение базируется на том, что перераспределение массы, вызванное перемещением крови и лимфы, а также смещением мышц вдоль продольной оси сегмента являются несущественными. При анализе движений туловища такое допущение нежелательно, так как во многих случаях может привести к значительным ошибкам.
Графический способ определения ЦМ звеньев тела и ОЦМ, при выполнении физических упражнений базируется на использовании таблицы Фишера — Бернштейна, где представлены сведения о положении ЦМ звеньев тела и их относительный вес в процентах (таб.4). Этот метод основан на сложении параллельных сил. Для определения равнодействующей двух параллельных сил соединяют прямой линией точки их приложения. На ней расположена точка приложения суммы двух сил, т. е. общий центр масс этих двух звеньев. Так, например, объединив ЦМ плеча и предплечья, получаем рычаг, на концах которого действуют параллельные силы F1 и F2 . Равнодействующая этих сил F3 , будет равняться:
Источник
Определение положения общего центра тяжести тела графическим способом (сложением сил тяжести)
Основные задачи: I) научиться определять положение центров тяжести звеньев (ЦТ); 2) научаться определять положение общего центра тяжести тела (ОЦТ).
Пояснения.
I. Центр тяжести звена – воображаемая точка, неизменно связанная со звеном, к которой приложена равнодействующая всех сил тяжести звена в любом его положении. Иначе говоря, моменты всех сил тяжести звена относительно его ЦТ взаимно уравновешиваются, их сумма равна нулю. Отсюда вытекают два способа определения положения ОЦТ двух и более звеньев: а) графический – сложением сил тяжести и б) аналитический – сложением моментов аил тяжести. Опытным путем (О. Фишер, Н.А. Бернштейн) были определены средние данные о весе звеньев тела и положений их ЦТ (табл. 6). Если принять вес тела за 100%, то вес каждого звена может быть выражен в относительных единицах (в процентах); при выполнении расчетов не обязательно знать абсолютный вес (в кг) ни всего тела, ни каждого звена. ЦТ звеньев определены по анатомическим ориентирам (голова, кисть и т.д.) или по относительному расстоянию ЦТ от проксимального сустава (радиус центра тяжести – часть всей длина звена конечности), или по пропорции туловища, стопы и др.
Относительный вес и расположение центров тяжести звеньев тела
| Название звена | Относительный вес Р (в %) | Расположение ЦТ звена |
| Голова | Над верхним краем наружного слухового отверстия | |
| Туловище | На линии между осями плечевых и тазобедренных суставов на расстоянии (от плечевой оси) 0,44 | |
| Плечо | 0,47 | |
| Предплечье | 0,42 | |
| Кисть | Пястно-фаланговый сустав третьего пальца | |
| Бедро | 0,44 | |
| Голень | 0,42 | |
| Стопа | На линии между пяточным бугром и вторым пальцем на расстоянии 0,44 от пятки |
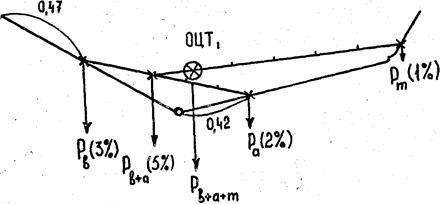
Рис. 8 Определение положения ЦТ двух звеньев руки сложением сил тяжести
2. Для определения равнодействующей двух параллельных сил соединяют прямой линией точки их приложения. При сложении сил тяжести двух звеньев эта линия соединяет их ЦТ. На этой линии располагается точка приложения суммы двух сил – равнодействующей, т.е. общий центр тяжести двух звеньев. Например, ЦТ плеча и предплечья расположен на линии, соединяющей ЦТ каждого (рис. 8). Так как плечо весит 3%, а предплечье 2% от веса тела (табл. 6), то эту линию следует разделить на 2+3=5 частей. ЦТ двух звеньев расположен ближе к более тяжелому (соотношение отрезков линии 2:3, считая от плеча). Таким способом можно определить общий центр тяжести тела, последовательно складывая силы тяжести, приложенные к каждому звену тела.
3. Положение ОЦТ и ЦТ звеньев важно определять при разборе условий равновесия в статическом положении. Изменения траектории движения ОЦТ тела могут происходить в результате действия внешних сил, приложенных к телу в целом, или внешних относительно соответствующего эвена, так как без действия внешней силы положение и движение ЦТ измениться не может.
Следует заметить, что сложение параллельных сил допустимо только в абсолютно твердом теле. Дело в том, что для деформируемого тела и материальной системы теорема о сложении параллельных сил неверна.
Две силы, приложенные к разным точкам, в этих случаях нельзя заменить одной силой. Поэтому, строго говоря, и общего центра тяжести и центра инерции (точка приложения равнодействующей параллельных сил инерции) в теле человека нет. Но есть совпадающая с ними точка – центр масс (точка, находящаяся внутри или вне тела, в которой пересекаются линии действия сил, приводящих данное тело или материальную систему в поступательное движение). Предполагая, что система мгновенно «отвердела», можно найти ее центр масс способами определения общего центра тяжести и рассматривать центр масс как центр тяжести.
Задания.
1. Определить положение ЦТ звеньев тела. На фотографии позы человека, пользуясь анатомическими данными, проставить положение проекции осей, суставов. Измерив длину каждого звена, помножить ее на соответствующее значение радиуса ЦТ. Пользуясь этими данными и анатомическими ориентирами, проставить ЦТ всех звеньев.
2. Найти равнодействующую всех сил тяжести. Удобно найти сначала ЦТ сил тяжести плеча и предплечья (векторы сил тяжести рисовать не нужно, следует только помнить относительный вес звеньев); далее, прибавив вес кисти, найти ОЦТ всей руки. Так же последовательно суммировать вес звеньев ноги. В нашем примере (рис. 9) положение симметричное; значит, ЦТ обеих рук расположены одинаково, так же, как и обеих ног. Определяя только ОЦТ всех конечностей, этого можно еще не учитывать, но, прибавляя к их весу вес туловища или головы, об этом нельзя забывать (удвоить вес конечности). Определяя положение ЦТ туловища, если оно согнуто или разогнуто, правильнее его положение наносить не на изогнутой продольной оси, а на прямой линии, соединяющей плечевой и тазобедренный суставы. Однако и здесь будет допущена погрешность, поэтому для точных научных исследований расчетные способы определения положения ОЦТ дают больший процент ошибок, чем экспериментальные (уравновешиванием).
 |
Рис. 9 Определение положения ОЦТ тела графическим способом
Определив положение ОЦТ головы и туловища (50% веса тела), а также всех конечностей (другая половина веса), расстояние между ними делят пополам. В этой точке и расположен ОЦТ тела.
Контрольные вопросы
1. Что такое центр тяжести эвена и общий центр тяжести тела?
2. Зачем нужно определение ЦТ и ОЦТ?
3. Какие основания имеет графический способ определения положения ОЦТ?
4. Какие данные необходимы для определения положения ОЦТ графическим способом?
5. Что такое центр инерции и центр масс тела, их отношение к положению ОЦТ?
Источник