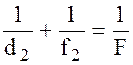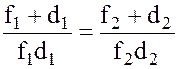Лабораторная работа №6
РМС 6. ОПРЕДЕЛЕНИЕ ФОКУСНЫХ РАССТОЯНИЙ ПОЛОЖИТЕЛЬНОЙ И ОТРИЦАТЕЛЬНОЙ ЛИНЗ МЕТОДОМ БЕССЕЛЯ
Цель работы — определение фокусных расстояний положительной и отрицательной линз методом Бесселя
Метод Бесселя
Общие сведения
Линзой называется прозрачное тело, ограниченное двумя криволинейными или криволинейной и плоской поверхностями. Обычно применяют линзы, поверхности которых имеют сферическую форму. Основные типы линз изображены на рис.1.
Рис. 1. Основные типы линз
На рисунке 1 представлены собирающие линзы (1 — двояковыпуклая, 2 — плосковыпуклая, 3 — вогнуто-выпуклая (положительный мениск)) и рассеивающие — (4 -двояковогнутая, 5 — плосковогнутая, 6 — выпукло-вогнутая (отрицательный мениск)).
Различают тонкие и толстые линзы. Линза называется тонкой, если её толщиной можно пренебречь по сравнению с радиусами кривизны её поверхностей.
Система, состоящая из одной или нескольких линз, называется центрированной, если центры кривизны всех её преломляющих поверхностей лежат на одной прямой, называемой оптической осью.
Вспомним основные свойства центрированной системы на примере толстой двояковыпуклой стеклянной линзы, находящейся в воздухе.
Лучи, проходящие через первый главный фокус F1, выходят с другой стороны линзы пучком, параллельным главной оптической оси ОО’ (рис. 2).
Рис. 2. Прохождение лучей, сходящихся в первом главном фокусе F1, через двояковыпуклую линзу
Главный фокус находится на расстоянии —f1 от первой главной плоскости Н1 которая определяется как геометрическое место точек пересечения падающих лучей с их продолжениями за линзой. Здесь и далее всем расстояниям, отсчитываемым против хода лучей, приписывается знак «-» (правило знаков).
Пучок лучей, падающих на линзу параллельно главной оптической оси, сходится во втором главном фокусе F2, отстоящем на расстоянии f2 от второй главной плоскости Н2
Рис. 2¢. Прохождение пучка лучей, параллельного оптической оси, через двояковыпуклую линзу
Если по обе стороны от линзы находится одна и та же среда, фокусные расстояния совпадают: f1 = f2 = f. Величина D = 1/f называется оптической силой линзы.
Собирающая линза сводит лучи, параллельные оптической оси в действительном фокусе f > 0, (рис. 2′), и имеет положительную оптическую силу.
Рис. 3. Прохождение пучка лучей, параллельного оптической оси, через рассеивающую линзу
Оптическая сила рассеивающей линзы отрицательна, так как для неё точка схождения параллельных лучей мнимая f 3rd Май 2009
Источник
Определение фокусных расстояний линз и оптических систем по методу Бесселя и с помощью коллимационной трубы
Страницы работы
Содержание работы
ЛАБОРАТОРНАЯ РАБОТА № 2
ОПРЕДЕЛЕНИЕ ФОКУСНЫХ РАССТОЯНИЙ ЛИНЗ И ОПТИЧЕСКИХ СИСТЕМ ПО МЕТОДУ БЕССЕЛЯ И С ПОМОЩЬЮ КОЛЛИМАЦИОННОЙ ТРУБЫ
Цель работы: научить студентов определять фокусные расстояния линз и оптических систем тремя методами:
1. метод Бесселя;
2. метод главной плоскости;
3. метод увеличения.
Приборы и принадлежности: оптическая скамья ОСК – 2 с измерительной линейкой, осветитель, коллиматор, суппорт с линзой в универсально вращающейся оправе, микроскоп со сменными окулярами (винтовой окулярный микрометр МОВ –1–15 х и окуляр увеличения 10 х ), миры, съёмная регулируемая щель, экран, универсальный держатель (рейтер), наборы линз, лампа подсветки с проецируемым предметом.
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ
Под сферической линзой понимают прозрачное тело, образованное пересечением сферических поверхностей, или сферических и плоских поверхностей. Если толщина линзы (расстояние между поверхностями линзы, взятое вдоль её главной оптической оси), мала по сравнению с радиусами кривизны её сферических поверхностей, то такая линза называется тонкой.
Прямая линия, проходящая через центры сферических поверхностей, называется главной оптической осью. Пучок световых лучей, распространяющийся параллельно главной оптической оси, после прохождения линзы пересекается в одной точке, называется главным фокусом линзы.
Расстояние от оптического центра линзы до фокуса, т.е. точки в которой пересекается пучок параллельных главной оптической оси лучей, называют главным фокусным расстоянием линзы. Фокусное расстояние является одной из основных характеристик линзы. Для тонкой линзы теория даёт формулу для нахождения фокусного расстояния линзы:
( 2.1 )
где d – расстояние от предмета до оптического центра линзы;
f – расстояние от изображения до оптического центра линзы;
F – фокусное расстояние линзы.
Величина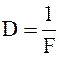 
называется оптической силой линзы. Оптическая сила измеряется в диоптриях. Одна диоптрия – это оптическая сила такой линзы, у которой фокусное расстояние равно 1м.
Если известны радиусы кривизны линзы R1, R2 и показатель преломления n вещества, из которого она изготовлена, то оптическая сила линзы равна:
( 2.2 )
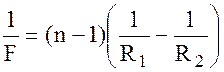
В современной оптике отдельные линзы собирают в оптические системы. Системы, в которых оптические центры всех линз расположены на одной прямой, называются центрированными. Простейшей оптической системой называется система, состоящая из двух линз, сложенных вплотную. Для такой системы оптическая сила D равна:
( 2.3 )
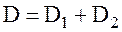
где D1 и D2 – оптические силы линз, входящих в систему.
Или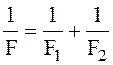 
( 2.4 )
Определение фокусных расстояний линз по формуле (2.1) затруднено, так как расстояния d и f отсчитываются от оптического центра линзы, лежащего внутри линзы. Существует ряд косвенных методов определения фокусного расстояния линз и оптических систем.
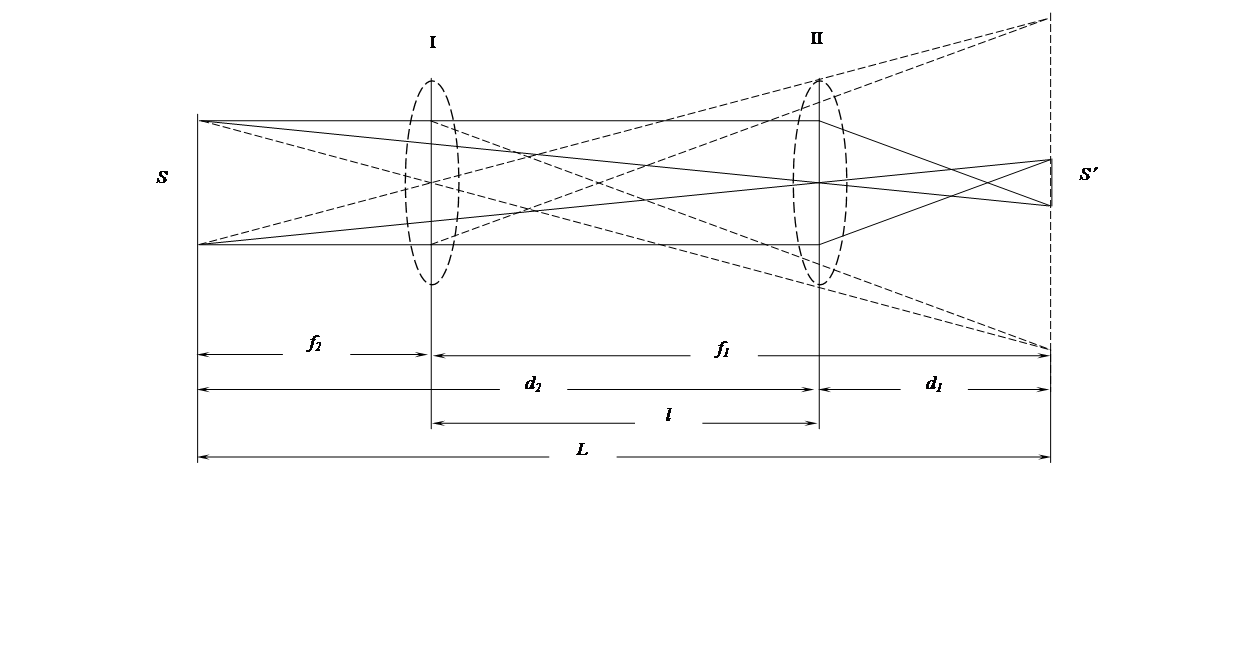
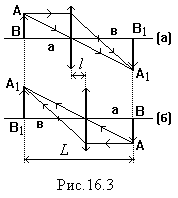
Одним из наиболее точных методов определения фокусных расстояний является метод Бесселя, заключающийся в следующем: на оптической скамье помещают предмет S и экран, на котором получается изображение предмета S’, даваемое линзой или системой линз, расположенной между предметом и экраном (рис. 2.1).
Если расстояние L от предмета до экрана достаточно велико и превышает учетверённое значение фокусного расстояния F , то, перемещая линзу или систему линз вдоль оптической оси, можно найти два таких положения линзы или системы 1 и 2 , при которых на экране наблюдаются чёткое увеличенное и уменьшенное изображения предмета.
Обозначим через d1 и f1 расстояния от линзы до предмета и от линзы до изображения при увеличенном изображении предмета и через d2 и f2 те же величины при уменьшенном его изображении. Из рис. 2.1 имеем:
( 2.5 )
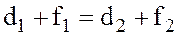
Запишем формулу (2.1) для увеличенного и уменьшенного изображений:
и 
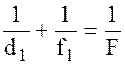
Откуда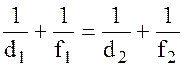 
или 
Так как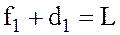 
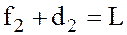
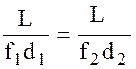
и 
, то
( 2.6 )
Из равенства (2.6) следует, что
( 2.7 )
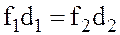
Равенства (2.5) и (2.7) одновременно выполняются только при условии, что
и 
( 2.8 )
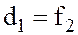
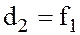
Обозначив расстояние между двумя положениями линзы, дающей увеличенное и уменьшенное изображение предмета через l, на основании (2.8) и рис. 2.1 получим:
; 
; 
; 
( 2.9 )
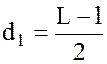
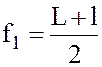
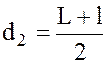
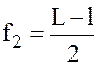
Подставляя (2.9) в (2.1) для каждого положения линзы 1 и 2 имеем:
( 2.10 )
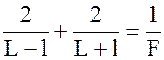
Отсюда фокусное расстояние F выразится зависимостью:
( 2.11 )
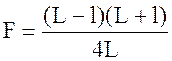
В соотношение (2.11) входят только величины L и l , равные расстоянию от предмета до экрана, и расстояния между двумя положениями линзы, легко измеряемые с достаточно большой степенью точности.
ОПИСАНИЕ УСТАНОВКИ
Установка для определения фокусных расстояний линз и оптических систем состоит из двух частей. Одна из них состоит из осветителя с изображаемым предметом (стрелкой), экрана, рейтера с закреплёнными в ней линзами, расположенных на противоположной от коллимационной трубы стороне, и предназначена для проведения исследований по методу Бесселя.
Вторая часть состоит из оптического рельса (1) с измерительной линейкой, на котором установлен длиннофокусный коллиматор (2)с мирой (3) или автоколлимационным окуляром со шкалой (рис. 2.2).
Подсветка миры или шкалы производится осветителем с лампочкой, питаемым от трансформатора. Испытуемые линзы или системы линз закрепляются в суппорте (4)с вращающейся универсальной оправой или на рейтере в специальном держателе. Наблюдение поверхности линз или изображений предметов осуществляют с помощью микроскопа (5)с винтовым окулярным микрометром, который размещают на оптическом рельсе. Микроскоп предусматривает смену окуляров (6).
Источник
Собирающей линзы методом Бесселя
Указанный выше метод определения главных фокусов является приближенным. Бессель предложил точный способ нахождения главных фокусных расстояний линз. Он заключается в том, что предмет и экран остаются неподвижными, а перемещается только линза, которую нужно устанавливать в двух положениях: в первом положении линза дает увеличенное изображение, а во втором положении линза дает уменьшенное изображение. Из формулы для нахождения фокусного расстояния собирающей линзы: 
видно, что величины аи вможно менять местами. Такая замена означает, что если на место изображения А1В1 в положении (б) (Рис.16.3) поставить предмет АВ из положения (а), то изображение в случае (б) предмета АВ получится в том же месте, где раньше был предмет. Исходя из рис.16.3.а и б, следует, что:
. Решая совместно эту систему уравнений относительно аив , получим:
. (16.4)
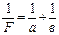
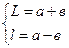
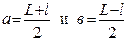
Подставляя (16.4) в (16.3), получим формулу нахождения главного фокусного расстояния собирающей линзы методом Бесселя: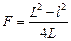 
. (16.5)
Порядок выполнения задания №2
1. На оптическую скамью поставить собирающую линзу и предмет.
2. Расположить экран и предмет на таком расстоянии друг от друга, чтобы, перемещая между ними линзу, можно было получить два отчетливых изображения (увеличенное и уменьшенное) предмета.
3. Измерить расстояние L (рис.16.3) между экраном и предметом.
4. Перемещая линзу, получить увеличенное изображение предмета на экране, заметить по линейке положение линзы. Затем, передвигая линзу, получить уменьшенное изображение предмета, заметить по линейке положение линзы. Вычислить расстояние l между двумя положениями линзы.
5. Меняя положение предмета и линзы, повторить измерения ещё два раза.
6. По формуле (16.5) вычислить фокусное расстояние. Рассчитать его среднее значение. Оценить погрешности измерений.
7. По среднему значению фокусного расстояния, по формуле (16.1) рассчитать оптическую силу линзы.
8. Результаты измерений и вычислений занести в таблицу 2.
| № | L, м | l, м | F, м | , м | DF, м | e, % | F= ± , м | , дптр |
Вычисления к заданию №2:
Контрольные вопросы защиты лабораторной работы:
1. Что называется линзой? Какие существуют типы линз?
2. Дайте определение фокуса линзы. Чем отличаются фокусные расстояния и оптические силы собирающей и рассеивающей линз?
3. Какие существуют виды аберраций? Как их устранить?
4. Нарисуйте и объясните принцип построения изображения в собирающей линзе.
5. Объясните принцип определения фокусного расстояния собирающей линзы двумя методами.
6. Запишите и объясните формулы: линзы, её фокусного расстояния и оптической силы.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
