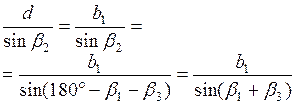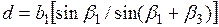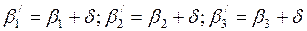Определение неприступных расстояний способом базисов

Определение неприступных расстояний способом базисов

Определение неприступных расстояний

В некоторых случаях, вследствие каких-либо препятствий, измерить линию продольного хода непосредственно лентой невозможно.

1 случай: (точка В недоступна для линейных измерений). По теореме синусов.

Разбиваем на местности ≈ равносторонний треугольник. Измеряем углы: β₁, β₂, β’₁, β’₂ и базисы b₁, b₂. Тогда неприступное расстояние АВ определяется по теореме синусов:

При заданной точности измерения базисов 1:2000, предельное расхождение между двумя определениями d не должно превышать 1:1000. За окончательное значение берется среднее из двух определений.

2 случай. По теореме косинусов:

Этот способ применяется, когда между точками A и В нет взаимной видимости. Разбиваем на местности примерно равнобедренные треугольники ABC и ABC₁.

Расстояние определяется по теореме косинусов. Расстояние определяется дважды.

Расхождение между двумя определениями допускается – 1/1500. За окончательное значение берется среднее из двух определений.

Источник

Определение неприступного расстояния

Решение некоторых инженерных задач

Неприступное расстояние – это расстояние до объекта, находящегося в поле зрения наблюдателя, которое не может быть измерено непосредственно. Это чаще всего связано с наличием на местности каких-то препятствий (забор, водоем и т.п.). В таком случае прибегают к косвенному способу измерений, когда измеряются какие-то дополнительные величины (линейные или угловые), а искомое расстояние вычисляется с их помощью.

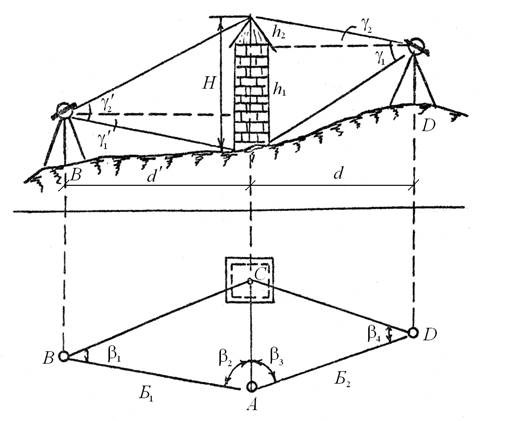
Неприступное расстояние определяют, как правило, из системы двух треугольников, построенных на основе измеренных базисов. Базисы разбивают на слабопересеченной местности, длина их должна быть не менее половины измеряемого расстояния. Базисные расстояния измеряют лентой или рулеткой с точностью 1/2000–1/3000, углы – теодолитом полным приемом. Схема определения неприступного расстояния показана на рис. 1.1.

Рис. 1.1. Схема определения неприступного расстояния и высоты сооружения

Из решения треугольников ABC и ADC определяют неприступное расстояние по формулам:

; (1.1)

. (1.2)

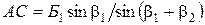
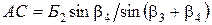
Относительная погрешность двух вычисленных значений неприступного расстояния не должна превышать 1/1000. При этом условии неприступное расстояние принимается равным среднему арифметическому двух вычисленных.

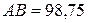
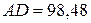
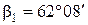
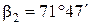
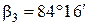
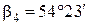
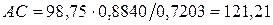
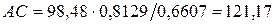
Например, м, м, , , , . Вычисляем неприступное расстояние м; м. Среднее значение неприступного расстояния м.

Источник

Измерение неприступных расстояний

При выполнении измерительных работ нередко возникают ситуации, когда та или иная линия не может быть измерена непосредственно, например, рулеткой (водные преграды, непроходимые болота и т.д.).

Определение неприступных расстояний способом базисов (рис. 52).

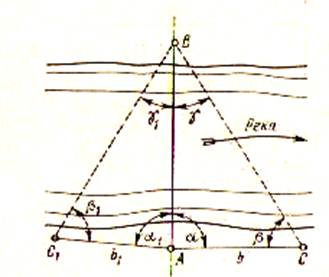
На удобных участках местности для производства линейных измерений с использованием рулетки от точки А измеряемой линии строят два базиса b и b₁ таким образом, чтобы между ними и измеряемой прямой линией образовались два треугольника с углами при основании не менее 30° и не более 150°. Базисы измеряют рулеткой дважды и при допустимых расхождениях в промерах определяют среднее значение каждого из них. Полным приемом теодолита измеряют углы при основаниях полученных треугольников АВС₁ и АВС, соответственно α₁, β₁ и α, β. По теореме синусов дважды определяют значение искомого неприступного расстояния:

АВ = b · ( sin β : sin γ ) или АВ’ = b₁ · ( sin β₁ : sin γ₁ ),

Если относительная погрешность между двумя измерениями не превышает допустимой (АВ — АВ’) : АВ_ср ≤ 1/ N_доп, то окончательно принимают в качестве искомого результата среднее значение АВ = (АВ + АВ’) : 2

Рис. 52. Схема определения неприступного расстояния способом базисов

Например: Вычислить непреступное расстояние АВ (ширину реки по результатам измерения):

b = 157, 30 м, α = 51°17′, β = 70°04′,

Найдем величину углов γ и γ₁.

γ = 180° — ( 51°17′ + 70°04′) = 58°39′,

γ₁ = 180° — ( 52°50’30′′ + 70°08′) = 57°01’30′′.

Неприступное расстояние АВ вычислим по теореме синусов

АВ = b · ( sin β : sin γ ) или АВ’ = b₁ · ( sin β₁ : sin γ₁ ),

АВ = 157,30 · (sin 70°04′ : sin 58°39′) = 173,16 м,

АВ’ = 154,40 ( sin 70°08′ : sin 57°01’30′′ ) = 173,09м.

Относительную погрешность двух измерений определяют

(АВ — АВ’) : АВ_ср = (173,16 – 173,09) : 173,125 = 0,07 : 173,125 = 1 : 2500,

Источник

Определение недоступных расстояний.

Так, для определения недоступного расстояния d измеряют лентой длину базиса b (рис. 8.3, а, б) и углы a и b . Из DABC находят

d = b sin a / sin (a + b),

где учтено, что sin g = sin (180°-a-b) = sin (a + b).

Рис. 8.3. Определение недоступного расстояния

Для контроля расстояние d определяют ещё раз из треугольника ABC₁ и при отсутствии недопустимых расхождений вычисляют среднее.

8.3. Нитяный дальномер

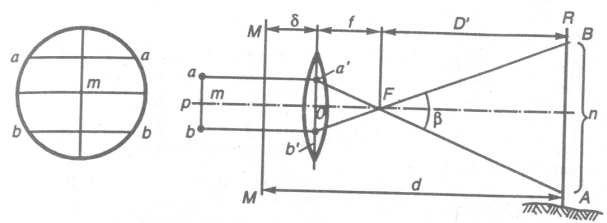
Теория нитяного дальномера. Зрительные трубы многих геодезических приборов снабжены нитяным дальномером. Сетка нитей зрительной трубы, кроме основных штрихов (вертикальных и горизонтальных), имеет дальномерные штрихи a и b (рис. 8.4, а). Расстояние D от оси вращения прибора MM (рис. 8.4, б) до рейки AB равно

где L — расстояние от фокуса объектива до рейки; f — фокусное расстояние; d — расстояние между объективом и осью вращения прибора.

Лучи, идущие через дальномерные штрихи сетки a и b параллельно оптической оси, преломляются объективом, проходят через его фокус F и проецируют изображения дальномерных штрихов на точки A и B, так что дальномерный отсчёт по рейке равен n. Обозначив расстояние между дальномерными штрихами p, из подобных треугольников ABF и a¢b¢F находим L = n f / p. Обозначив f / p = K и f + d = c , получаем

где K — коэффициент дальномера и c — постоянная дальномера.

Рис. 8.4. Нитяный дальномер: а) – сетка нитей; б) – схема определения расстояния

При изготовлении прибора f и p подбирают такими, чтобы K=100, а постоянная c была близкой к нулю. Тогда D = 100 n.

Точность измерения расстояний нитяным дальномером » 1/300.

Определение горизонтального проложения линии, измеренной нитяным дальномером. При измерении наклонной линии отсчёт по рейке это отрезок n = AB (рис. 8.5). Если бы рейку наклонить на угол n, то отсчёт был бы равен n₀ = A₀B₀ = n cosn и наклонное расстояние D=Kn₀+c = Kn×cosn+c.

Рис. 8.5. Измерение нитяным дальномером наклонного расстояния

Умножив наклонное расстояние D на cosn, получим горизонтальное расстояние d = K n cos 2 n + c cos n.

Прибавив и отняв с× cos 2 n, после преобразований получим

Вторым слагаемым по его малости пренебрежем. Получим

Вычисления упрощаются, если воспользоваться составленными с использованием этой формулы «Тахеометрическими таблицами».

Источник

Определение неприступных расстояний

ТЕМА 6

Линейные измерения. Компарирование. Порядок измерения линий на местности. Приведение длин наклонных линий к горизонту. Вешение линий.

Линейные измерения, т.е. измерения длины линий на местности могут выполняться непосредственно и косвенно. При непосредственном методе мерный прибор (измерительную рулетку, землемерную ленту и т.п.) последовательно укладывают в створе измеряемого отрезка. При косвенном методе измеряют вспомогательные параметры (углы, базисы, физические параметры), длину отрезка вычисляют по формуле, отображающей зависимость между измеренными величинами и длиной отрезка.

Точность определения расстояний зависит от метода измерений, применяемого прибора, условий измерений и может колебаться от 1:200 до 1:1000000 (миллионной) измеряемого расстояния.

В результате измерений расстояний на местности должны быть получены их горизонтальные проложения – проекции на уровенную поверхность.

Конечные точки измеряемой на местности линии закрепляются знаками. На пунктах государственной геодезической сети устанавливают каменные, бетонные или железобетонные монолиты, трубы, рельсы на точках съёмочной сети – деревянные столбы и колья или металлические штыри. Длина кольев 30-40 см, толщина 4-6 см. Кол, закрепляющий точку, забивают почти вровень с землей и в верхний срез кола вбивают гвоздь, для центрирования прибора при измерениях. Для отсекания точки рядом забивают второй кол – сторожок, на котором записывают номер обозначаемой им точки. Для лучшей видимости рядом устанавливают веху.

В городских условиях на улицах и тротуарах с покрытием точки закрепляют железными гвоздями или костылями или обозначают краской на покрытии дороги.

Линии, намечаемые для непосредственного измерения, по возможности, должны проходить по местности, удобной для измерения. В процессе измерений мерный прибор укладывают в створе измеряемой линии на глаз или с помощью теодолита. При длинах линий более 150 м их предварительно провешивают, устанавливая в створе ряд дополнительных вех. На равнинной местности вехи ставят через 70-100 м, на холмистой через 20-50м.

Створ- это линия пересечения местности вертикальной плоскостью, проходящей через концы отрезка линии.

Веха – деревянный шест длиной до 2,5 м и толщиной 3,5-4см, раскрашенный полосками красного и белого цветов. Нижняя часть вехи заострена.

Приемы вешения

а) между взаимно видимыми точками А и В. Веха ставиться за точку в створе линии.

А 4 3 2 1 вешение на себя

б) При вешении через гору

с d

в) Вешение через овраг

А 2 3

В

Для непосредственного измерения линий служат ленты, рулетки, проволоки. Различают ленты шкаловые и штриховые. Наиболее употребительным мерным прибором является стальная 20-метровая штриховая лента со шпильками. Лента представляет собой тонкую стальную полосу длиной 20 м. С ручками на концах. Ширина ленты 10-15 мм, толщина 0,3-0,5 мм. Ее длина считается от одного начального штриха до другого (конечного). Штрихи находятся на концах ленты у вырезов для установки шпилек.

Метры на линии отмечены металлическими пластинами, а полуметры заклепками. Счет делений ведется на обеих сторонах ленты. Наименьшее деление – дециметр — отверстие. Отсчет по ленте производится с точностью до 1 см. К ленте придается комплект стальных шпилек из 11 штук (или 6) и для удобства надеваются на железное кольцо.

Для измерения расстояний используются также рулетки – стальные и тесьняные длиной 5, 10, 20 и 50 м. И шкаловые ленты (10-15см шкала с сантиметровыми делениями.

Перед измерением должна быть определена действительная длина мерного прибора путем сравнения с известной длиной контрольного прибора. Такое сравнение называется компарированием, оно производится на компараторах.

Для стальных мерных лент компараторы устраивают в виде гладкого деревянного бруса. На концах бруса имеются шкалы, расстояние между нулями которых точно известно. Ленты укладывают на компаратор, натягивают и по шкалам определяют их длину. Нередко применяются полевые компараторы. Для этого, на ровном месте, на расстоянии около 120 м устанавливают прочные знаки с отмеченными точками, расстояние между которыми измеряют более точным прибором. Измеряя затем многократно это расстояние лентой, определяют фактическую длину ленты.

Измерение линий осуществляют два человека. Задний мерщик прикладывает нуль ленты к начальной точке линии, закрепляет ленту шпилькой и направляет переднего мерщика по створу линии. Передний мерщик держит ленту вытянутой рукой, не закрывая собой переднюю точку измеряемого отрезка линии. После укладки ленты в створе её встряхивают, натягивают и в вырез ленты на переднем конце вертикально ставят шпильку. Далее задний мерщик вынимает свою шпильку, а передний снимает ленту со своей шпильки, и оба мерщика протягивают ленту вперед по направлению створа и весь процесс повторяется.

При вычислении длины линии в её измеренное значение вводят поправки.

1) за компарирование мерного прибора

2) за приведение к горизонту

3) за температуру

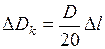
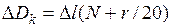
Поправка за компарирование мерной ленты вычисляется по формуле или ,

где D – длина измеренной линии в м; N = число отложений

— разность фактической длины ленты и номинала в м; знак поправки зависит от знака = l_ф – l_н,

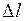
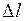
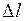
поправку 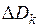алгебраически прибавляют к результату измерения.

Для нахождения горизонтального проложения d надо знать величину угла наклона ν, тогда или , .

Если на измеряемой линии имеются участки с различными углами наклона, то для каждого из них, измерение углов и определение поправок производится отдельно.

Поправка за температуру вводится по формуле ,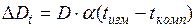

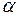
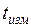
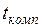
где – линейный коэффициент расширения стали 12·10 -6

– средняя t ˚ в период измерения линии

– температура в период компарирования.

Поправку вводят при >8 ˚

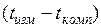
Для контроля, оценки и повышения точности измерений каждую линию измеряют дважды : в прямом и обратном направлении или двумя лентами в одном направлении. Окончательный результат получается как среднее из двух измерений, если точность измерения характеризуется относительными ошибками.

1:2000 в благоприятных условиях,

1:1000 в неблагоприятных условиях.

Ошибка 1:200 означает, что расхождение в измерении линии длиной 100 м в прямом и обратном направлении должно быть не более 5 см.

Окончательное горизонтальное проложение с учетом всех поправок вычисляют по формуле 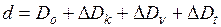. Пример

Косвенные методы измерения расстояний. При косвенном измерении расстояний измеряют вспомогательные параметры: углы, базисы, физические параметры и т.д.

К косвенным методам относятся измерения расстояний нитяным дальномерам, светодальномером, вычисление расстояния по углам и базисам и т.п.

Рассмотрим измерение расстояний светодальномером. Светодальномер – это электроннооптический прибор, предназначенный для измерения расстояний с использованием электромагнитных волн. Измерение расстояния светодальномером сводится к следующему: на одной из конечных точек А устанавливают приемопередатчик, который излучает электромагнитные колебания и направляет их на отражатель, расположенный на другом конце линии. Отражатель принимает световой поток и направляет его обратно к приемопередатчику. Приемопередатчик фиксирует моменты выхода t₁ и возвращения t₂ светового потока. Таким образом световой поток в интервале времени 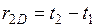пройдет расстояние D в прямом и обратном направлениях. Зная скорость υ распространения электромагнитных колебаний, можно записать .

Время 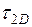можно измерить непосредственно или через какой-либо параметр, являющийся функцией временного интервала.

В СССР выпускается три группы светодальномеров:

1. Светодальномеры большой дальности действия (15-50км) с погрешностью измерения расстояния порядка ± (5-10)мм + (1-2) мм/км. Они предназначены для измерения сторон в государственных геодезических сетях.

2. Светодальномеры малой дальности (1-3 км) с погрешностью измерения расстояния около 20 мм. Они предназначены для измерения расстояний в геодезических сетях сгущения и для топографических съёмок.

3. светодальномеры повышенной точности для измерения коротких расстояний (0,3-3 км) с погрешностью около 2 мм и менее.

В современных приборах задачи управления, вычисления и контроля решаются с помощью микро ЭВМ. После наведения прибора на отражатель нажимают кнопку запуска и измерения производятся автоматически по заданной программе. При возможности измерения вертикального угла выполняется редуцирование наклонного расстояния на горизонтальную плоскость.

Наибольшее распространение в строительном производстве нашли светодальномеры СМ5 и его усовершенствованная модель СМ5 «Блеск».

Определение неприступных расстояний

На практике некоторые линии пересекают реки, овраги, котлованы строящихся зданий, широкие траншеи и другие препятствия. Так как эти линии обычным способом измерить трудно, то их называют неприступными.

Для определения неприступного расстояния АВ = d в треугольнике АВС измеряют базис АС=в₁ и углы β₁ β₃. По теореме синусов

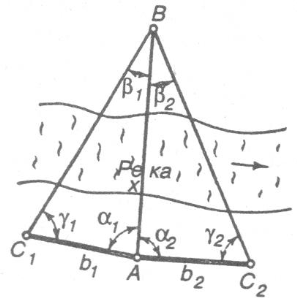
или

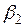
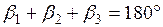
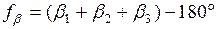
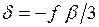
Для контроля измеряют угол . В треугольнике АВС должно соблюдать-ся условие . В результате влияния погрешностей измерения углов это условие нарушается. Величину отклонения суммы углов от теоретического значения называют угловой невязкой. Невязку распределяют с обратным знаком поровну на все углы треугольника. Для этого вычисляют поправку , а затем исправленные углы

Вычисление длины неприступного расстояния осуществляют с исправленными значениями углов. Точность определения неприступных расстояний зависит во многом от формы углов треугольника, наилучшим считается равносторонний треугольник (угол при точке В>30˚.

Для повышения точности и исключения грубых ошибок длину неприступного расстояния рекомендуется определить из двух треугольников АВС и АВЕ. Если по линии АВ нет видимости и невозможно измерить углы в точках А и В, то измеряют длины сторон а,в и угол β, а длину неприступной линии вычисляют по формуле .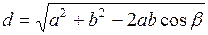

Нитяной дальномер

Принцип измерения расстояний дальномерами основан на решении прямоугольного треугольника, в котором по малому параллактическому углу «β» и к противолежащему катету «в» (базису) определяют длину другого катета 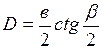. Для упрощения измерений одну из этих величин делают постоянной, а другую измеряют. Если величина «в» постоянна, а величину«β» измеряют, то это дальномер с постоянным базисом. Если величина «β» постоянна, а измеряют «в», то это дальномер с постоянным углом.

Наибольшее распространение в геодезической практике нашел нитяной дальномер. Это дальномер с постоянным параллактическим углом и переменным базисом. Этот дальномер имеется в зрительных трубах геодезических приборов и состоит из двух горизонтальных штрихов, называемых дальномерными нитями, расположенных симметрично относительно центрального штриха сетки нитей.

В комплект дальномера входит дальномерная рейка с делениями. Если в начальную точку А установить прибор, а в точку В дальномерную рейку, то искомое расстояние будет равно (1). Из подобия треугольников МFN и аFв имеем откуда , где – отсчет, соответствующий числу делений дальномерной рейки, видимых в трубу между дальномерными нитями;

– фокусное расстояние объектива;

– расстояние между дальномерными нитями.

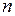
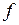
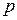
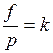
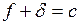
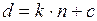
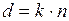
Отношение для данного прибора постоянно и называется коэффициентом дальномера. Кроме того будем считать, что –постоянное слагаемое дальномера. Тогда в соответствии с (1) получим . В современных теодолитах, имеющих трубы с внутренней фокусировкой, постоянное слагаемое «с» близко к нулю. Пренебрегая этой величиной, получим . (2). Коэффициент дальномера обычно равен 100, что соответствует углу β = 34,38 ‘

Источник