Определение неприступного расстояния способом базисов

Определение неприступного расстояния способом базисов

Определение неприступных расстояний

В некоторых случаях, вследствие каких-либо препятствий, измерить линию продольного хода непосредственно лентой невозможно.

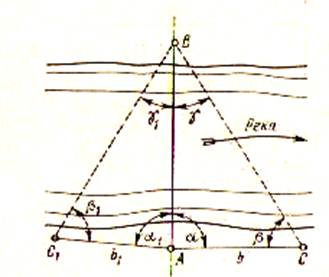
1 случай: (точка В недоступна для линейных измерений). По теореме синусов.

Разбиваем на местности ≈ равносторонний треугольник. Измеряем углы: β₁, β₂, β’₁, β’₂ и базисы b₁, b₂. Тогда неприступное расстояние АВ определяется по теореме синусов:

При заданной точности измерения базисов 1:2000, предельное расхождение между двумя определениями d не должно превышать 1:1000. За окончательное значение берется среднее из двух определений.

2 случай. По теореме косинусов:

Этот способ применяется, когда между точками A и В нет взаимной видимости. Разбиваем на местности примерно равнобедренные треугольники ABC и ABC₁.

Расстояние определяется по теореме косинусов. Расстояние определяется дважды.

Расхождение между двумя определениями допускается – 1/1500. За окончательное значение берется среднее из двух определений.

Источник

Измерение неприступных расстояний

При выполнении измерительных работ нередко возникают ситуации, когда та или иная линия не может быть измерена непосредственно, например, рулеткой (водные преграды, непроходимые болота и т.д.).

Определение неприступных расстояний способом базисов (рис. 52).

На удобных участках местности для производства линейных измерений с использованием рулетки от точки А измеряемой линии строят два базиса b и b₁ таким образом, чтобы между ними и измеряемой прямой линией образовались два треугольника с углами при основании не менее 30° и не более 150°. Базисы измеряют рулеткой дважды и при допустимых расхождениях в промерах определяют среднее значение каждого из них. Полным приемом теодолита измеряют углы при основаниях полученных треугольников АВС₁ и АВС, соответственно α₁, β₁ и α, β. По теореме синусов дважды определяют значение искомого неприступного расстояния:

АВ = b · ( sin β : sin γ ) или АВ’ = b₁ · ( sin β₁ : sin γ₁ ),

Если относительная погрешность между двумя измерениями не превышает допустимой (АВ — АВ’) : АВ_ср ≤ 1/ N_доп, то окончательно принимают в качестве искомого результата среднее значение АВ = (АВ + АВ’) : 2

Рис. 52. Схема определения неприступного расстояния способом базисов

Например: Вычислить непреступное расстояние АВ (ширину реки по результатам измерения):

b = 157, 30 м, α = 51°17′, β = 70°04′,

Найдем величину углов γ и γ₁.

γ = 180° — ( 51°17′ + 70°04′) = 58°39′,

γ₁ = 180° — ( 52°50’30′′ + 70°08′) = 57°01’30′′.

Неприступное расстояние АВ вычислим по теореме синусов

АВ = b · ( sin β : sin γ ) или АВ’ = b₁ · ( sin β₁ : sin γ₁ ),

АВ = 157,30 · (sin 70°04′ : sin 58°39′) = 173,16 м,

АВ’ = 154,40 ( sin 70°08′ : sin 57°01’30′′ ) = 173,09м.

Относительную погрешность двух измерений определяют

(АВ — АВ’) : АВ_ср = (173,16 – 173,09) : 173,125 = 0,07 : 173,125 = 1 : 2500,

Источник

Как определяют неприступное расстояние?

Неприступное расстояние – это расстояние до объекта, находящегося в поле зрения наблюдателя, которое не может быть измерено непосредственно. Это чаще всего связано с наличием на местности каких-то препятствий (забор, водоем и т.п.). В таком случае прибегают к косвенному способу измерений, когда измеряются какие-то дополнительные величины (линейные или угловые), а искомое расстояние вычисляется с их помощью.

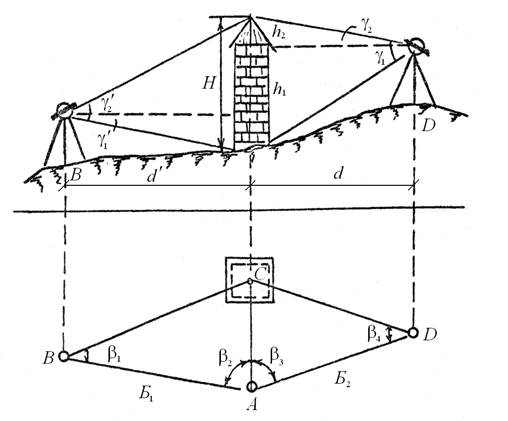
Неприступное расстояние определяют, как правило, из системы двух треугольников, построенных на основе измеренных базисов. Базисы разбивают на слабопересеченной местности, длина их должна быть не менее половины измеряемого расстояния. Базисные расстояния измеряют лентой или рулеткой с точностью 1/2000–1/3000, углы – теодолитом полным приемом. Схема определения неприступного расстояния показана на рис. 1.1.

Рис. 1.1. Схема определения неприступного расстояния и высоты сооружения

Из решения треугольников ABC и ADC определяют неприступное расстояние по формулам:

; (1.1)

. (1.2)

Относительная погрешность двух вычисленных значений неприступного расстояния не должна превышать 1/1000. При этом условии неприступное расстояние принимается равным среднему арифметическому двух вычисленных.

Например, м, м, , , , . Вычисляем неприступное расстояние м; м. Среднее значение неприступного расстояния м.

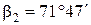
Чем определяется выбор метода создания высотного съемочного обоснования?

Комплекс работ, в результате выполнения которого получают карту или план местности, называют топографической съемкой. Рассмотрим один пример. Пусть нужно составить план некоторого участка местности (например, план небольшого дачного участка). Если требуется невысокая точность изображения деталей местности на плане, можно применить глазомерную съемку.

Наметим на местности точки-ориентиры (например, углы изгороди участка), определим их взаимное положение и нанесем в масштабе на бумагу — будущий план участка. Эти точки играют роль опорных, так как положение всех остальных точек (углы построек, грядки, отдельные деревья и кусты) мы будем определять относительно них или относительно линий, их соединяющих.

Инструментальная съемка выполняется с более высокой точностью, чем глазомерная, но принцип съемки остается тот же: на местности создается сеть опорных точек, взаимное положение которых в принятой системе координат определяют в первую очередь. Затем прибор для съемки устанавливают последовательно на каждую опорную точку и снимают ситуацию и рельеф в промежутках между ними, определяя положение точек местности относительно опорных точек и соединяющих их линий.

Точки, на которые устанавливают прибор для съемки, закрепляют на местности; их называют пунктами съемочного обоснования. Их координаты и отметки определяют из геодезических измерений, как правило, до начала съемки. По координатам эти пункты наносят на планшет, подготовленный к съемке (на планшете имеется только координатная сетка линий X=Const и Y=Const). Пункты геодезического съемочного обоснования образуют жесткий геометрический каркас плана, относительно которого определяется положение всех остальных точек плана.

По Инструкции средняя ошибка планового положения пунктов съемочного обоснования допускается 0.1 мм в масштабе плана. Этот допуск определяется точностью графических построений. Действительно, нет нужды определять координаты пунктов с большей точностью, так как они нужны только для того, чтобы нанести по ним на план пункты съемочного обоснования. Предельная ошибка планового положения пунктов съемочного обоснования допускается 0.2 мм в масштабе плана на застроенной территории и в открытой местности и 0.3 мм — в закрытой местности. При выполнении специальных съемок допуск на эту ошибку может быть уменьшен.

Средняя ошибка пунктов съемочного обоснования допускается 0.1*h, где h — высота сечения рельефа создаваемого плана.

Задание №2

Задача 1

Вычислить дирекционные углы линий ВС и СD, если известны дирекционный угол α _АВ линии АВ и измеренные правые по ходу углы β₁ и β₂ (рис.1)

Исходные данные

1. Дирекционный угол α _АВ = 20 0 35,2 ´

2. Первый угол при точке В (между сторонами АВ и ВС) β₁ = 189°59,2´, первый угол при точке С (между сторонами ВС и CD) β₂ = 159°28,0´.

Решение

Дирекционные углы вычисляются по правилу: дирекционный угол последующей стороны равен дирекционному углу предидущей стороны плюс 180 0 и минус горизонтальный угол, справа по ходу лежащий. Следовательно, α _ВС = α _АВ + 180 — β₂ ; α _CD = α _ВС + 180 — β₁.

α _ВС = α _АВ + 180 — β₁ = 20 0 35,2 ´+ 180 — 189°59,2´ = 10º36´

α _CD = α _ВС + 180 — β₂ = 10º36´+ 180 — 159°28,0´ = 31º08,0´

α _АВ = 20 0 35,2 ´

α _ВС = 10 0 36,0 ´

α _CD = 31º08,0 ´

Задача 2

Найти координаты Х_С и Y_C точки С (рис. 1), если известны координаты Х_В и Y_В точки В, длина (горизонтальное положение) d_ВС линии ВС и дирекционный угол α _ВС этой линии.

Исходные данные

Решение

Координаты точки С вычисляются по формулам:

∆х = d ∆y = d

∆х_ВС = d_{ВС ВС} ; ∆y_ВС = d_{ВС ВС}

Перевод дирекционных углов в румбы

Номер четверти	Название четверти	Формула перевода	Номер четверти	Название четверти	Формула перевода
I	СВ	I= αI	III	ЮЗ	III= αIII-180º
II	ЮВ	II=180º- αII	IV	СЗ	IV=360º- αIV

Знаки приращения прямоугольных координат

СВ ЮВ ЮЗ СЗ ∆х + — — + ∆y + + — —

_ВС = α _ВС = 10º36´ — СВ

∆х_ВС = 239,14 х cos10º36´ = 235,06м

∆y_ВС = 239,14 х 10º36´ = 43,99м

Х_С = -14,02 + 235,06 = 221,04м

Y_С = 627,98 + 43,99 = 671,97м

Задание 3

Составление топографического плана строительной площадки

По данным полевых измерений составить и вычертить топографический план строительной площадки в масштабе 1:2000 с высотой сечения рельефа 1м.

1. Теодолитно-высотный ход между двумя пунктами полигонометрии ПЗ 8 и ПЗ 19 с измеренными длинами сторон и углами (Рисунок 2., табл.1).
2. Координаты полигонометрических знаков ПЗ 8 и ПЗ 19. Данные приняты по результатам вычисления координат в задаче№2.

Y _{ПЗ 8} = 627,98 м

Результаты измерений углов и длин сторон хода

Номер вершин хода

Измеренные углы (правые)

Длины сторон (горизонтальное проложение), м

Источник