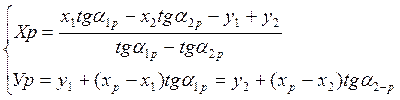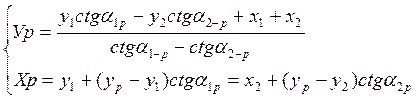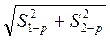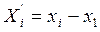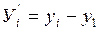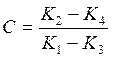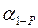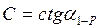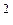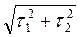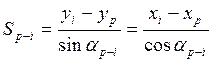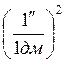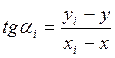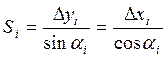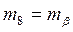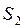Определение координат точки способом засечек
Прямая угловая засечка
1) Прямая угловая засечка применяется в тех случаях, когда характер местности не позволяет, либо сильно затрудняет измерение линейных расстояний между точками, или искомая точка находится на значительном расстоянии от исходных пунктов.
Для определения координат точки Р необходимо измерить точным теодолитом углы на исходных пунктах 1 и 2 (β1 и β2) между стороной АВ и направлением на точку Р. Кроме того, нужны координаты исходных пунктов 1 и 2.
Координаты искомой точки можно определить по формулам Юнга:
(1)
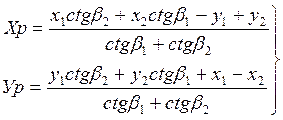
Если мы используем внутренние углы β1, β2, βІ. В случае использования при вычислении дирекционных углов направлений с исходных пунктов на искомую точку применяются формулы Гаусса (формулы тангенсов):
(2) 
Если α близко к 90° и 270° применяются формулы котангенсов:
(3)
СКП планового положения определяемой точки рассчитывается по формуле:
(4), где γ – угол засечки
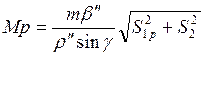
γ = 180° – (β1 +β2) = α1р – α2р
ВЕДОМОСТЬ ВЫЧИСЛЕНИЯ ПРЯМОЙ УГЛОВОЙ ЗАСЕЧКИ (ПО ФОРМУЛАМ ЮНГА)
S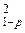 
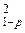
= ∆х +∆у
S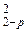 
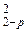
= ∆х+ ∆у
Для контроля применяются многократные прямые засечки с 3-х и более пунктов. При этом для каждого определённого значения координат точки Р определяют все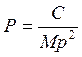 
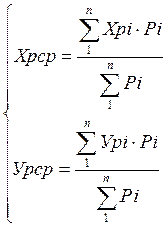
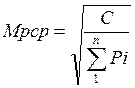
, где С ≈ 1. За конечные значения координат берут средневзвешенное из всех найденных значений координат.
(5) 
(6)
Обратная однократная угловая засечка. Способ Кнейселя.
Нумерация по часовой стрелке.
За начало координат принимается пункт №1, затем находят условные координаты остальных исходных точек X’і и У’і
По условным координатам и измеренным углам β1 и β2 вычисляют коэффициенты:
(7)
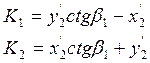
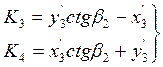
Геометрическая сущность коэффициента С – котангенс 
Затем определяются условные координаты искомой точки:
(8)
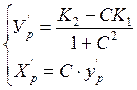
Координаты искомой точки будут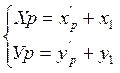 
(9)
СКП планового положения точки Р определяется по формуле:
(10)
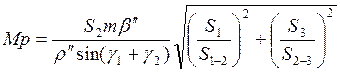
ВЕДОМОСТЬ ВЫЧИСЛЕНИЯ ОБРАТНОЙ УГЛОВОЙ ЗАСЕЧКИ (ПО ФОРМУЛАМ КНЕЙСЕЛЯ)
1+C
Как видно из формулы, Мр резко возрастает, если сумма γ1 + γ2 близки к 0° и 180°.
В первом случае точка лежит на прямой между пунктами 1, 2, 3 , во втором – на круге.
оптимально 30° Приближёнными .
обозначим их хр, ур;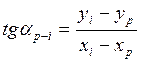 
;
свободные члены уравнений поправок:
, где 
(11)
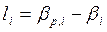
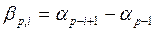
Здесь βp, i – приближённое значение измерения углов,
βi – измеренные углы
Находим коэффициенты уравнения поправок
(12) 
, где 
(13)
(14)
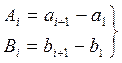
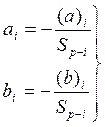
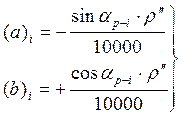
Уравнение поправок: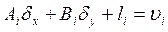 
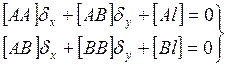
(15)
(16)
Поправки δx и δy к приближённым значениям координат и веса координат Рх и Ру вычисляются по уравнениям:
(17)
(18) поправки δх и δу будут получены в дециметрах, Рх и Ру будут иметь размерность 
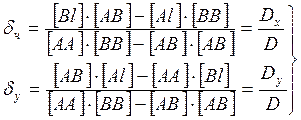
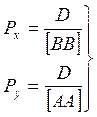
Правильность вычисления поправок определяется по формуле: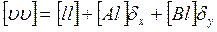 
(19)
Окончательные результаты вычислений координат:
(20)
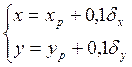
дирекционных углов 
расстояний 
исправленные углы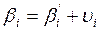 
(21)
СКП измеренного угла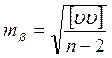 
, n – число углов (22)
СКП координат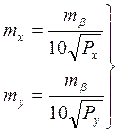 
(23)
Передача координат с вершины знака на землю
При построении съёмочной сети часто возникает необходимость снесения (передачи) координат с исходного пункта (точки привязки) на грунтовый пункт. Это связано с тем, что исходным пунктом часто бывают постоянные предметы местности с известными координатами, например – труба котельной, водонапорная башня и т. д. с которых невозможно произвести угловые измерения. Для этого выбирается и закрепляется на местности точка Р с которой удобно производить измерения и намечают два базиса: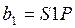 
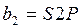
и 
. Конечные точки (1 и 2) закрепляют кольями. В полученных треугольниках АР1 и АР2 углы при точке А должны быть не 150°.
Для решения этой задачи базисы измеряют с относительной погрешностью не более 1/2000, углы в треугольниках S1, β1, S2, γ точным теодолитом полным приёмом. Кроме того, необходимо знать координаты пункта В.
Вначале по теореме синусов определяют расстояние SAP
(1) 
по двум треугольникам
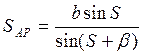
Длину линии АВ (L) и дирекционный угол αАВ находить из решения обратной геодезической задачи:
; 
(2)
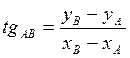
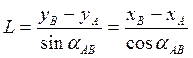
контрольная формула для αAB:
(3)
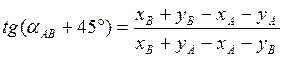
Углы μ и λ и дирекционный угол αАВ вычисляют по следующим формулам:
(4), (5), (6)
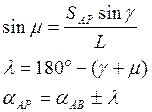
Теперь, решая прямую геодезическую задачу можно вычислить координаты точки Р:
(7)
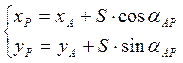
Для контроля вычисляются дирекционный угол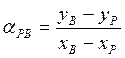 
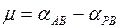
(8) и угол 
(9)
СКП вычисленного значения SPA
(10)
– СКП измерения базиса
и 
– СКП измерения углов 
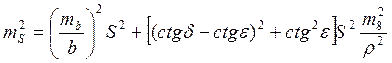
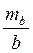
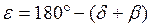
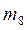
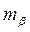
Предельно допустимое расхождение между значениями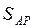 
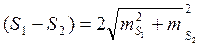
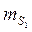
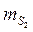
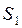
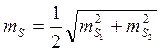
, полученное по двум базисам:
и 
– СКП 
и 
(11)
СКП вычисленного значения дирекционного угла 
(12)
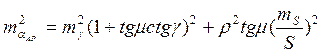
Источник
Определение координат засечками.
Для определения планового положения точки необходимо измерить два элемента. Для контроля, кроме необходимых, выполняют избыточные измерения. Засечки различают прямые, обратные и комбинированные. В прямой засечке измерения выполняют на исходных пунктах (рис. 6.6 a, г); в обратной – на определяемом пункте (рис. 6.6 б, д); в комбинированной – на исходных и определяемом пунктах (рис. 6.6 в). В зависимости от вида измерений засечки бывают угловые (рис. 6.6 a, б, в), линейные (рис. 6.6 г), линейно-угловые (рис. 6.6 д). Измеренные углы на рис. 6.6 отмечены дугами, измеренные расстояния – двумя штрихами.
Рассмотрим вычисление координат в некоторых засечках.
Прямая угловая засечка. На исходных пунктах A и B с координатами 
, 
, 
, 
. (рис. 6.6 а) измеряют углы 
и 
. При обработке измерений сначала вычисляют дирекционные углы направлений AP и BP:
; 
.
Дирекционные углы с координатами связаны формулами обратной геодезической задачи
; 
.
Решая эти уравнения относительно xp и yp, получим формулы, по которым вычисляют координаты определяемой точки Р (формулы Гаусса):
; (6.5)
.
Для контроля ординату yP вычисляют вторично по формуле:
.
Рис. 6.6. Схемы засечек: а – прямая угловая; б – обратная угловая; в – комбинированная угловая; г – линейная; д – линейно-угловая
Если один из дирекционных углов 
или 
близок к 
или 
, то вместо формул (6.5 – 6.7) вычисления выполняют по формулам
;
.
Для контроля аналогичные измерения и вычисления выполняют, опираясь на другую исходную сторону BC. За окончательные значения координат определяемой точки принимают средние.
Существуют и иные формулы решения прямой угловой засечки, например, формулы котангенсов углов треугольника (формулы Юнга):
; 
.
Обратная угловая засечка. На определяемой точке P (рис. 6.6 б) измеряют углы 
и 
между направлениями на исходные пункты A, B и C. При этом исходные пункты выбирают такие, чтобы они с точкой P не оказались на одной окружности или вблизи нее. Координаты точки P вычисляют по формулам Гаусса (6.5 — 6.7), предварительно вычислив дирекционные углы:
; 
.
Для контроля измеряют избыточный угол 
и вычисляют координаты, используя другую пару измеренных углов.
Линейная засечка. Для определения координат точки Р (рис. 6.6 г) измеряют расстояния d1, d2. По формуле косинусов (6.1) находят углы треугольника АРВ. Вычисляют дирекционный угол aАР = aАВ — ÐA, а затем по формулам прямой геодезической задачи — искомые координаты
Для контроля измеряют избыточное расстояние d 3 и вычисляют координаты из другого треугольника ВРС.
Источник
