Определение количества информации алфавитным способом
Вокруг нас везде и всюду происходят информационные обмены. Информацией обмениваются между собой люди, животные, технические устройства, органы человека или животного и т.д. во всех этих случаях передача информации происходит в виде последовательностей различных сигналов. В вычислительной технике такие сигналы кодируют определенные смыс ловые символы, т.е. такие сигналы кодируют последовательности знаков — букв, цифр, кодов цвета точек и т.д. С этой точки зрения рассматривается другой подход к измерению информации — алфавитный.
Каким образом в этом случае можно найти количество информации?
канал передачи информации
Формула связывает между собой количество возможных информационных сообщений N и количество информации I, которое несет полученное сообщение. Тогда в рассматриваемой ситуации N — это количество знаков в алфавите знаковой системы, а I — количество информации, которое несет каждый знак: N = 2 I .
С помощью этой формулы можно, например, определить количество информации, которое несет знак в двоичной знаковой системе:
Таким образом, буква русского алфавита несет 5 битов информации (при алфавитном подходе к измерению количества информации).
Количество информации, которое несет знак, зависит от вероятности его получения. Если получатель заранее точно знает, какой знак придет, то полученное количество информации будет равно 0. Наоборот, чем менее вероятно получение знака, тем больше его информационная емкость.
В русской письменной речи частота использования букв в тексте различна, так в среднем на 1000 знаков осмысленного текста приходится 200 букв «а» и в сто раз меньшее количество буквы «ф» (всего 2). Таким образом, с точки зрения теории информации, информационная емкость знаков русского алфавита различна (у буквы «а» она наименьшая, а у буквы «ф» — наибольшая).
Количество информации в сообщении. Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации.
Если знаки несут одинаковое количество информации, то количество информации Iс в сообщении можно подсчитать, умножив количество информации I3, которое несет один знак, на длину кода (количество знаков в сообщении) К:
Информация и информационные процессы
Так, каждая цифра двоичного компьютерного кода несет информацию в 1 бит. Следовательно, две цифры несут информацию в 2 бита, три цифры — в 3 бита и т. д. Количество информации в битах равно количеству цифр двоичного компьютерного кода (табл. 1.3).
Количество информации, которое несет двоичный компьютерный код.
Двоичный компьютерный код
Символов на нашей клавиатуре около 200 (русский и латинский алфавит, строчные и прописные буквы, цифры, знаки препинания, спецсимволы). Попробуем подобрать число n, достаточное для кодирования этих символов: 27 = 128 (мало), 28 = 256 (хватит). Поэтому в кодировке ASCII 1 символ текста кодируется одним байтом (8 битами).
Количество данных, обрабатываемых компьютером, измеряется в байтах, но чаще для этого используются более крупные единицы:
1 Килобайт (Кб) = 2 10 байт = 1024 байт
1 Мегабайт (Мб) = 2 10 Кб = 1 048 576 байт
1 Гигабайт (Гб) = 2 10 Мб = 1 073 741 824 байт.
Может возникнуть вопрос, почему в международной системе СИ приставки Кило, Мега и Гига вдруг получили другое значение. Ответ здесь в больших буквах. Кило и кило — это две большие разницы.
1 килобайт (кб) = 10 3 байт = 1 000 байт
1 мегабайт (мб) = 10 6 байт = 1 000 000 байт
1 гигабайт (гб) = 10 9 байт = 1 000 000 000 байт.
В ноябре 2000 г. международной электротехнической комиссией (МЭК) были приняты поправки к международному стандарту. По этому решению приставки, кратные степеням 2 получили своё особое название:
1 кибибайт (Киб)= 2 10 байт = 1024 байт
1 мебибайт (Миб) = 2 10 Киб = 1 048 576 байт
1 гибибайт (Гиб)= 2 10 Миб = 1 073 741 824 байт
К сожалению, эти приставки не стали привычными нашему слуху, хотя срок их существования уже достаточно большой.
Постановлением Правительства Российской Федерации от 31 октября 2009 г. № 879 закреплено обозначение двоичных приставок в привычном звучании, но написание их отличается от десятичных.
Скорость передачи данных и пропускную способность каналов связи принято измерять в битах в секунду (бит/с) и кратных этому:
1 килобит (кбит/с) = 10 3 бит/с
1 мегабит (мбит/с) = 10 6 бит/с
1 гигабит (гбит/с) = 10 9 бит/с
А при измерении оперативной памяти принято измерение в единицах, кратных не степеням десятки, а степеням двойки.
Из-за этого первоначально и возникла путаница в приставках.
Источник
Измерение информации: алфавитный подход
Описание презентации по отдельным слайдам:
Описание слайда:
Измерение информации: алфавитный подход
Информация и информационные процессы
Описание слайда:
Как измерить информацию?
Вопрос: «Как измерить информацию?» очень непростой.
Ответ на него зависит от того, что понимать под информацией. Но поскольку определять информацию можно по-разному, то и способы измерения тоже могут быть разными.
ИНФОРМАЦИЯ
Описание слайда:
Алфавитный подход к измерению информации
Познакомимся с способом измерения информации, который не связывает количество информации с содержанием сообщения, и называется он алфавитным подходом.
При алфавитном подходе к определению количества информации отвлекаются от содержания информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.
Применение алфавитного подхода удобно прежде всего при использовании технических средств работы с информацией. В этом случае теряют смысл понятия «новые — старые», «понятные — непонятные» сведения. Алфавитный подход является объективным способом измерения информации в отличие от субъективного содержательного подхода.
Описание слайда:
Алфавит и его мощность
Все множество используемых в языке символов будем традиционно называть алфавитом.
Обычно под алфавитом понимают только буквы, но поскольку в тексте могут встречаться знаки препинания, цифры, скобки, то мы их тоже включим в алфавит. В алфавит также следует включить и пробел, т.е. пропуск между словами.
Полное количество символов алфавита принято называть мощностью алфавита.
Будем обозначать эту величину буквой N. Например, мощность алфавита из заглавных русских букв и отмеченных дополнительных символов равна 54.
АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЬЪЭЮЯ0123456789(). «»:-; (пробел)
Описание слайда:
Сколько информации несет один символ в русском языке
Представьте себе, что текст к вам поступает последовательно, по одному знаку, словно бумажная ленточка, выползающая из телеграфного аппарата. Предположим, что каждый появляющийся на ленте символ с одинаковой вероятностью может быть любым символом алфавита.
В каждой очередной позиции текста может появиться любой из N символов.
Тогда, согласно известной нам формуле 2I = N , каждый такой символ несет I бит информации, которое можно определить из решения уравнения: 2I = 54.
Получаем: I = 5.755 бит.
Вот сколько информации несет один символ в русском тексте!
П Р И В Е Т ! К А К Д
Описание слайда:
Количество информации в тексте
А теперь для того, чтобы найти количество информации во всем тексте, нужно посчитать число символов в нем и умножить на I.
Посчитаем количество информации на одной странице книги.
Пусть страница содержит 50 строк. В каждой строке — 60 символов. Значит, на странице умещается 50×60=3000 знаков. Тогда объем информации будет равен: 5,755 х 3000 = 17265 бит.
При алфавитном подходе к измерению информации количество информации зависит не от содержания, а от размера текста и мощности алфавита.
Описание слайда:
Задание 1:
Определите информационный объем страницы книги, если для записи текста использовались только заглавные буквы русского алфавита, кроме буквы Ё.
Решение:
N = 32
2I = N
2I = 32
I = 5
На странице 3000 знаков, тогда объем информации = 3000 * 5 = 15000 бит.
Описание слайда:
Двоичный алфавит
А что если алфавит состоит только из двух символов 0 и 1?
В этом случае: N = 2; 2I = N; 2I = 2; I = 1!
При использовании двоичной системы (алфавит состоит из двух знаков: 0 и 1) каждый двоичный знак несет 1 бит информации.
Интересно, что сама единица измерения информации «бит» получила свое название от английского сочетания
«binary digit» — «двоичная цифра».
Описание слайда:
Достаточный алфавит
Удобнее всего измерять информацию, когда размер алфавита N равен целой степени двойки. Например, если N=16, то каждый символ несет 4 бита информации потому, что 24 = 16. А если N =32, то один символ «весит» 5 бит.
Ограничения на максимальный размер алфавита теоретически не существует. Однако есть алфавит, который можно назвать достаточным. С ним мы скоро встретимся при работе с компьютером. Это алфавит мощностью 256 символов. В алфавит такого размера можно поместить все практически необходимые символы: латинские и русские буквы, цифры, знаки арифметических операций, всевозможные скобки, знаки препинания.
Поскольку 256 = 28, то один символ этого алфавита «весит» 8 бит. Причем 8 бит информации — это настолько характерная величина, что ей даже присвоили свое название — байт.
1 байт = 8 бит
Описание слайда:
Количество информации в тексте
Сегодня очень многие люди для подготовки писем, документов, статей, книг и пр. используют компьютерные текстовые редакторы. Компьютерные редакторы, в основном, работают с алфавитом размером 256 символов.
В этом случае легко подсчитать объем информации в тексте. Если 1 символ алфавита несет 1 байт информации, то надо просто сосчитать количество символов; полученное число даст информационный объем текста в байтах.
Пусть небольшая книжка, сделанная с помощью компьютера, содержит 150 страниц; на каждой странице — 40 строк, в каждой строке — 60 символов.
Значит страница содержит 40×60=2400 байт информации.
Объем всей информации в книге: 2400 х 150 = 360 000 байт.
Описание слайда:
Более крупные единицы информации
Описание слайда:
Скорость передачи информации
Прием-передача информации могут происходить с разной скоростью.
Количество информации, передаваемое за единицу времени, есть скорость передачи информации или скорость информационного потока.
Очевидно, эта скорость выражается в таких единицах, как бит в секунду (бит/с), байт в секунду (байт/с), килобайт в секунду (Кбайт/с) и т.д.
Описание слайда:
Вопросы:
Что такое «алфавит»? Что такое «мощность алфавита»?
Как определяется количество информации в сообщении с алфавитной точки зрения?
Что больше 1 Кбайт или 1000 байт?
Расположите единицы измерения информации в порядке возрастания:
Гигабайт; Байт; Мегабайт; Килобайт.
Сколько информации содержится в сообщении, если для кодирования одного символа использовать 1 байт:
«Компьютер – универсальный прибор.»
Два текста содержат одинаковое количество символов. Первый текст составлен в алфавите мощностью 32 символа, второй – мощностью 64 символа. Во сколько раз отличается количество информации в этих текстах?
Описание слайда:
Задание 2:
Племя Мумбу-Юмбу использует алфавит из букв: αβγδεζηθλμξσφψ, точки и для разделения слов используется пробел.
Сколько информации несет свод законов племени, если в нем 12 строк и в каждой строке по 20 символов?
Описание слайда:
Задание 3:
Вычислите какова мощность алфавита, с помощью которого записано сообщение, содержащее 2048 символов, если его объем составляет 1.25 Кбайта.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Источник
Алфавитный подход к определению количества информации
Тип урока: Объяснение нового материала (01.10.08)
Формировать у учащихся понимание алфавитного подхода к измерению информации.
Развивать операциональное мышление и коммуникативную компетентность при обработке информации.
Воспитывать восприятие компьютера как инструмента информационной деятельности человека и бережного отношения к компьютеру.
I. Организационный момент.
II. Актуализация знаний.
III. Изложение нового материала.
V. Подведение итогов урока.
VI. Домашнее задание.
Урок проводится в компьютерном классе, доска, мел.
Основные понятия: алфавит, мощность алфавита, информационный вес символа в алфавите, производные единицы измерения информации.
I. Организационный момент
Учитель приветствует учащихся и отмечает отсутствующих.
II. Актуализация знаний
• Какое событие можно назвать информативным?
(событие информативно при условии:
1) произошло как минимум одно из двух возможных событий;
2) информация понятна, достоверна, объективна, полезна.)
• В чем заключается содержательный подход к измерению информации?
(в содержательном подходе рассматривается информативность равновероятностных событий.)
• Какую формулу используют для нахождения количества информации?
(Для нахождения количества информации используют формулу:
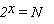
где N – количество всех возможных событий;
х – количество информации, содержащееся в данном сообщении.)•
Какую минимальную единицу используют для измерения количества информации?
(в качестве минимальной единицы информации используется 1 бит информации.)
Учитель предлагает детям ответить на следующие вопросы:
Сколько символов в компьютерном алфавите?
Как найти количество информации в тексте?
III. Изложение нового материала.
Вы научились определять количество информации, которое содержится в сообщениях, уменьшающих неопределенность наших, т.е. мы рассматривали информацию со своей точки зрения – с позиции человека. Для нас количество информации зависит от ее содержания, понятности и новизны. Однако любое техническое устройство не воспринимает содержание информации. Здесь не работают «неопределенность знаний» и «вероятность информации». Поэтому в вычислительной технике используется другой подход к измерению информации – алфавитный.
Алфавитный подход к измерению информации позволяет определить количество информации, заключенной тексте. Алфавитный подход является объективным, т.е. он не зависит от субъекта (человека), воспринимающего текст.
Множество символов, используемых при записи текста, называется алфавитом. Полное количество символов в алфавите называется мощностью (размером) алфавита. Если допустить, что все символы алфавита встречаются в тексте с одинаковой частотой (равновероятно), то количество информации, которое несет каждый символ, вычисляется по формуле:

Если весь текст состоит из К символов, то при алфавитном подходе размер содержащейся в нем информации равен:
где i — информационный вес одного символа в используемом алфавите,
К— количество символов в тексте,
I – количество информации, содержащейся в тексте (информационный объем текста).

Сравнивая объемы информации русского текста и английского, мы видим, что на английском языке информации меньше, чем на русском. Но ведь содержание не изменилось! Следовательно, при алфавитном подходе к измерению информации ее количество не зависит от содержания, а зависит от мощности алфавита и количества символов в тексте. С точки зрения алфавитного подхода, в толстой книге информации больше, чем в тонкой. При этом содержание книги не учитывается.
Правило для измерения информации с точки зрения алфавитного подхода:
1) Найти мощность алфавита – N
2) Найти информационный вес одного символа i из уравнения 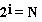
3) Найти количество символов в тексте — К
4) Найти количество информации – I (информационный объем всего сообщения)
Для измерения больших объемов информации используют следующие единицы:
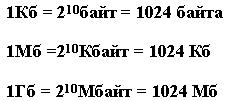
Книга, набранная с помощью компьютера содержит 150 страниц; на каждой странице – 40 строк, в каждой строке – 60 символов. Каков объем информации в книге?
Значит, страница содержит 40*60=2400 байт информации.
Объем всей информации в книге (в разных единицах):
2 400*150=360 000 байт; 360 000/1024=351,5625Кб; 351,5625/1024=0,34332275Мб
Ответьте на вопросы, поставленные в начале урока.
1) Сколько символов в компьютерном алфавите?
(Алфавит из 256 символов используется для представления текстов в компьютере).
2) Как найти количество информации в тексте?
(Чтобы найти количество информации в тексте надо:
1. Найти мощность алфавита – N
2. Найти информационный вес одного символа i из уравнения 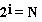
3. Найти количество символов в тексте — К
4. Найти количество информации – I (информационный объем всего сообщения)
Вычислите информационный объем сообщения: Наступили холода, при условии, что один символ кодируется 1 байтом.
(Решение: K = 16, i = 1 байт, следовательно I = 16 байт = 16*8 бит = 128 бит)
3Кб в байтах и битах (3*1024байт = 3072байт*8 = 24576 бит)
5920 бит в байтах и Кб (5920 бит/8 =740 байт/1024=0,72Кб)
1. Наиболее объективным методом измерения информации является алфавитный подход
2. Информативность сообщения зависит от мощности используемого алфавита
3. При измерении информации рассматриваются объекты окружающего мира, описанные языковыми средствами.
VI. Подведение итогов урока.
Учитель выставляет оценки учащимся, выполнявшим задания у доски, комментируя их.
VII. Домашнее задание.
И.Семакин «Информатика» Базовый курс Учебник 7-9 классы § 4. Вопросы и задания стр. 24-25.
По желанию, выполнить творческое задание:
Составить кроссворд по теме «Определение количества информации».
Место работы: школьный медиокласс по расписанию его работы.
Источник







