Определение функции одной переменной область определения способы задания

Тема 1. ФУНКЦИЯ ОДНОЙ ПЕРЕМЕННОЙ

1.1. Определение функции одной переменной

Определение. Пусть даны два множества X и Y. Если каждому элементу x из множества X по некоторому правилу f соответствует единственный элемент y из множества Y, то говорят, что на множестве X определена функция y = f ( x ) с областью определения X = D( f ) и областью изменения Y = E ( f ). При этом x считают независимой переменной, или аргументом функции, а y – зависимой переменной или функцией.

Частным значением функции y = f ( x ) при фиксированном значении аргумента x = x₀ называют y ₀ = f ( x ₀ ).

Графиком функции y = f ( x ) называют геометрическое место точек M ( x ; f ( x )) на плоскости Oxy , где x Î D ( f ) и f ( x ) Î E ( f ).

1.2. Способы задания функции

1) Аналитический способ – способ задания функции с помощью формулы.

Различают несколько способов аналитического задания функции:

а) Функция задана явно формулой y = f ( x ).

Например: 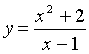, где D( y ) = (– ∞;1) (1;+∞).

б) Функция задана неявно уравнением, связывающем x и y : F( x ; y ) = 0.

Например: – уравнение окружности с центром в начале координат и радиусом r . Если из этого уравнения выразить y через x , то получится две функции:

и ,

которые имеют область определения , а области значений этих функций будут: для первой – , для второй – .

в) Функция задана параметрически с помощью некоторого параметра t , причём и аргумент x , и функция y зависят от этого параметра:

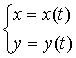
Например: можно задать окружность с помощью параметрических уравнений:

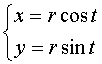
2) Табличный способ задания функции – например, таблицы Брадиса задают функции y = sin x , y = cos x и др.

3) Графический способ задания функции, когда зависимость функции от её аргумента задаётся графически.

1.3. Сложная и обратная функции

Определение 1 . Пусть функция y = f ( U) определена на множестве D( f ), а функция U = g ( x ) определена на D( g ), причём E( g ) D( f ).

Тогда функция y = F( x ) = f ( g ( x )) называется сложной функцией (или функцией от функции, или суперпозицией функций f и g ) .

Определение 2 . Пусть задана функция y = f ( x ) взаимно однозначно отображающая множество X = D ( f ) на множество Y = E ( f ). Тогда функция x = g ( y ) называется обратной к функции y = f ( x ), т. е. любому y E( f ) соответствует единственное значение x D ( f ), при котором верно равенство y = f ( x ).

Замечание. Графики функций y = f ( x ) и x = g ( y ) представляют одну и ту же кривую. Если же у обратной функции независимую переменную обозначить x , а зависимую y , то графики функций y = f ( x ) и y = g ( x ) будут симметричны относительно биссектрисы первого и третьего координатных углов.

1.4. Элементарные функции

Основные элементарные функции:

y = const ( постоянная функция), D ( y ) = R ; E ( y ) = c .

( линейная функция), D ( y ) = R ; E ( y ) = R .

y = ( степенная функция), α Î R , E( y ), D ( y ) зависят от α .

y = ( показательная функция), a > 0, a ≠ 1, D ( y ) = R , E ( y ) = ( 0; +∞).

y = ( логарифмическая функция) ), a > 0, a ≠ 1, D ( y ) = (0;+∞), E ( y ) = R .

y = sin x , D ( y ) = R , E ( y ) = .

y = cos x, D( y) = R, E( y) = .

y = tg x, D( y) = , E( y) = R.

y = ctg x, D( y) = , E( y) = R.

Обратные тригонометрические функции :

y = arcsin x , D ( y ) = , E ( y ) = .

y = arccos x, D( y) = , E( y) = .

y = arctg x , D ( y ) = R , E ( y ) = .

y = arcctg x , D ( y ) = R , E ( y ) = .

Элементарной функцией называется функция, составленная из основных элементарных функций с помощью конечного числа операций сложения, вычитания, умножения, деления и суперпозиции.

Например: – элементарная функция.

Графики обратных тригонометрических функций:

Источник

Определение функции и способы ее задания

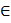
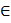
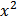
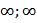
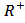
(Определение: Пусть X и Y – числовые множества. Если каждому элементу x X по некоторому правилу f поставлен в соответствие единственный элемент y Y, то говорят, что на множестве X определена функция y=f(x). x=D(f) – область значения; y= ; x=(- )=R; E(f)= =[0;+ )

способы задания: 1) Аналитический способ(формулой); 2) Графический способ(график); 3) Табличный способ; 4) Словесное описание.)

Функция- зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у, где переменная х- независимая переменная или аргумент и переменная у- зависимая переменная

Способы задания функций

Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции. Рассмотрим некоторые способы задания функций.

Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.

При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции.

Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.

Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.

Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами — наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.

Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции.

Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.

Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.

Источник