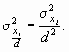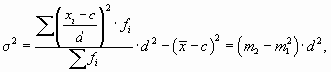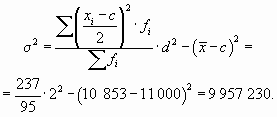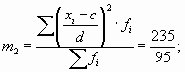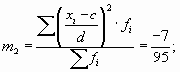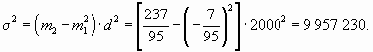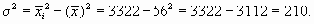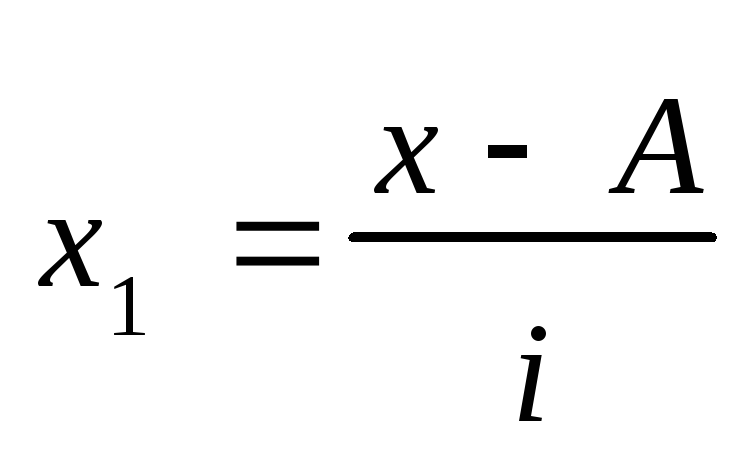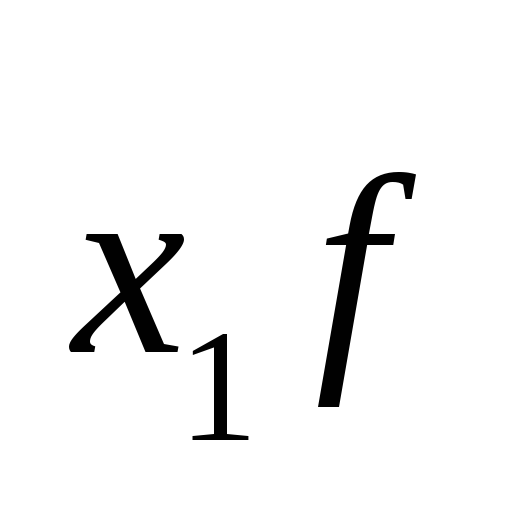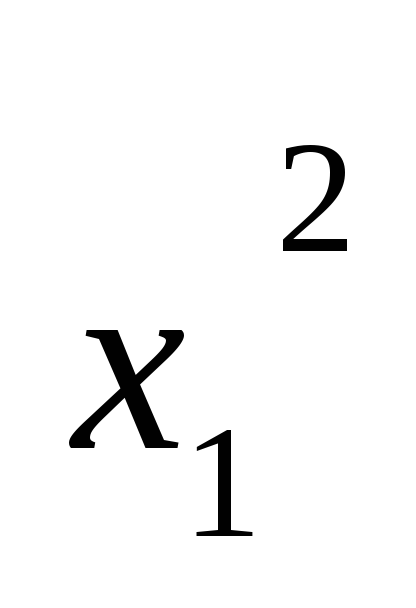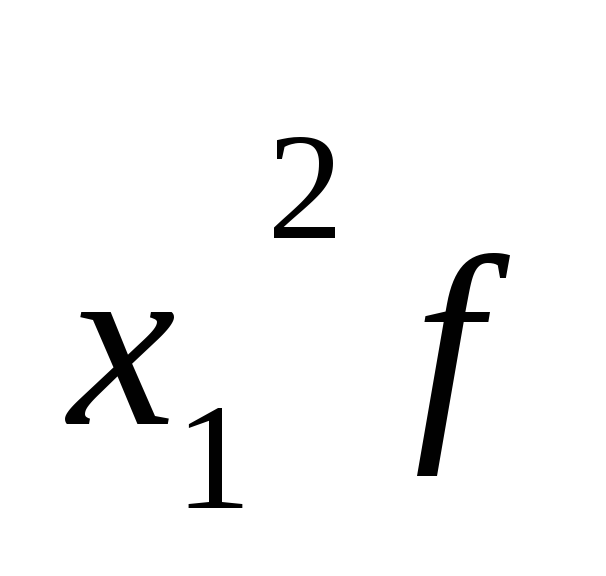- Показатели вариации в статистике
- 7.2. Свойства дисперсии, расчет дисперсии способом моментов
- Вопросы и ответы
- Показатели вариации в статистике
- 7.2. Свойства дисперсии, расчет дисперсии способом моментов
- Вопросы и ответы
- 6.2. Вычисление дисперсии и среднего квадратического отклонения «способом моментов»
- 6.3. Внутригрупповая и межгрупповая вариации
Показатели вариации в статистике
7.2. Свойства дисперсии, расчет дисперсии способом моментов
Дисперсия обладает рядом математических свойств. Приведем основные из них:
- если xi = c, где с — постоянная величина, то дисперсия будет равна нулю;
- если из всех значений признака вычесть постоянную величину с, то дисперсия от этого не изменится:
На приведенных свойствах дисперсии основан один из методов ее расчета — способ моментов. Согласно ему, дисперсию можно вычислить по следующей формуле (применяется только в случае вариационных рядов с равными интервалами):
где с — значение середины интервала, находящегося в центре ряда (если количество интервалов четное, то берется середина интервала из центра ряда с наибольшей частотой);
d — величина интервалов;
— момент второго порядка;
— момент первого порядка.
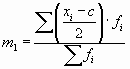
По данным табл. 7.5 определим дисперсию способом моментов.
 |
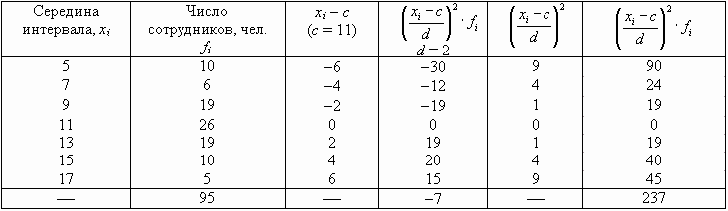Если при расчете дисперсии способом моментов взять за постоянную величину с нуль, а за d — единицу, то приведенная выше формула примет следующий вид:
Таким образом получаем, что дисперсия равна разности между средней из квадратов индивидуальных значений признака и квадрата средней.
Применим данный способ расчета дисперсии. Пусть известно, что средняя арифметическая величина, рассчитанная для вариационного ряда, равна 56 дол., а средний квадрат его индивидуальных значений — 3322. Определим дисперсию.
Вопросы и ответы
Мне нужно изучить математическую статистику с нуля для обработки данных на компьютере. Читаю уже вторую лекцию, но пока ничего даже отдалённо близкого к моей цели не нахожу. Есть ли математическая статистика в дальнейших лекциях? Или я зря теряю время на изучение этого курса? У меня крайне ограниченный временной срок — я не могу терять время на самостоятельную проверку моего вопроса посредством изучения данного курса.
Источник
Показатели вариации в статистике
7.2. Свойства дисперсии, расчет дисперсии способом моментов
Дисперсия обладает рядом математических свойств. Приведем основные из них:
- если xi = c, где с — постоянная величина, то дисперсия будет равна нулю;
- если из всех значений признака вычесть постоянную величину с, то дисперсия от этого не изменится:
На приведенных свойствах дисперсии основан один из методов ее расчета — способ моментов. Согласно ему, дисперсию можно вычислить по следующей формуле (применяется только в случае вариационных рядов с равными интервалами):
где с — значение середины интервала, находящегося в центре ряда (если количество интервалов четное, то берется середина интервала из центра ряда с наибольшей частотой);
d — величина интервалов;
— момент второго порядка;
— момент первого порядка.
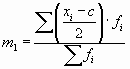
По данным табл. 7.5 определим дисперсию способом моментов.
| |
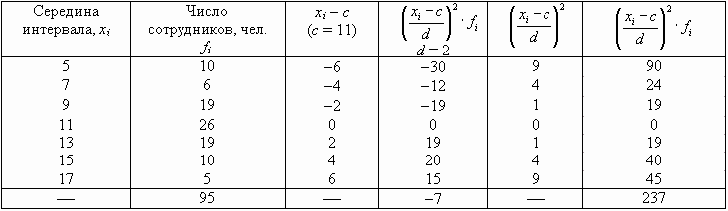Если при расчете дисперсии способом моментов взять за постоянную величину с нуль, а за d — единицу, то приведенная выше формула примет следующий вид:
Таким образом получаем, что дисперсия равна разности между средней из квадратов индивидуальных значений признака и квадрата средней.
Применим данный способ расчета дисперсии. Пусть известно, что средняя арифметическая величина, рассчитанная для вариационного ряда, равна 56 дол., а средний квадрат его индивидуальных значений — 3322. Определим дисперсию.
Вопросы и ответы
Мне нужно изучить математическую статистику с нуля для обработки данных на компьютере. Читаю уже вторую лекцию, но пока ничего даже отдалённо близкого к моей цели не нахожу. Есть ли математическая статистика в дальнейших лекциях? Или я зря теряю время на изучение этого курса? У меня крайне ограниченный временной срок — я не могу терять время на самостоятельную проверку моего вопроса посредством изучения данного курса.
Источник
6.2. Вычисление дисперсии и среднего квадратического отклонения «способом моментов»
«Способ моментов» основан на математических свойствах дисперсии. Для рядов распределения с равными интервалами расчет дисперсии можно произвести по следующей формуле:
,
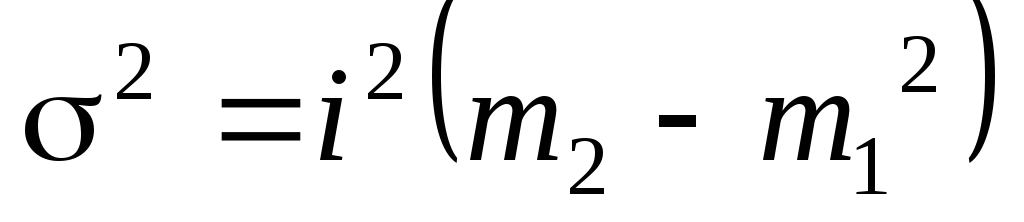
где i – размер интервала;
m1 – момент первого порядка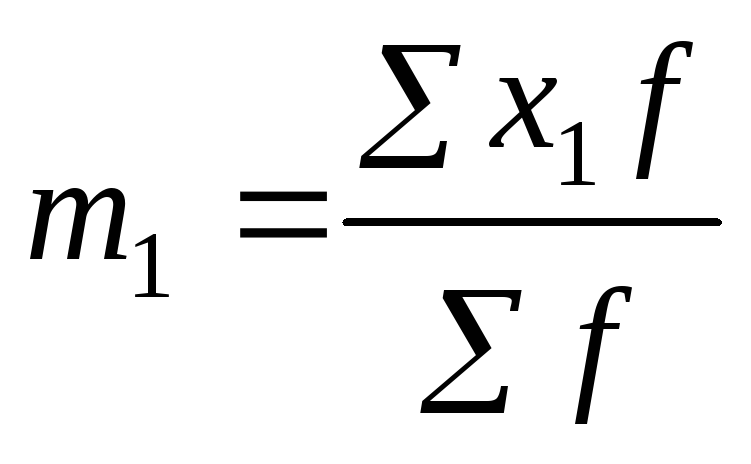 
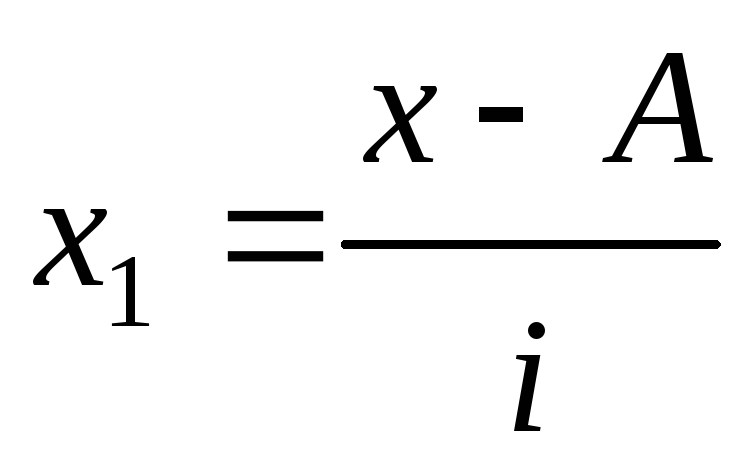
(х1 – упрощенные варианты; 
);
m2 – момент второго порядка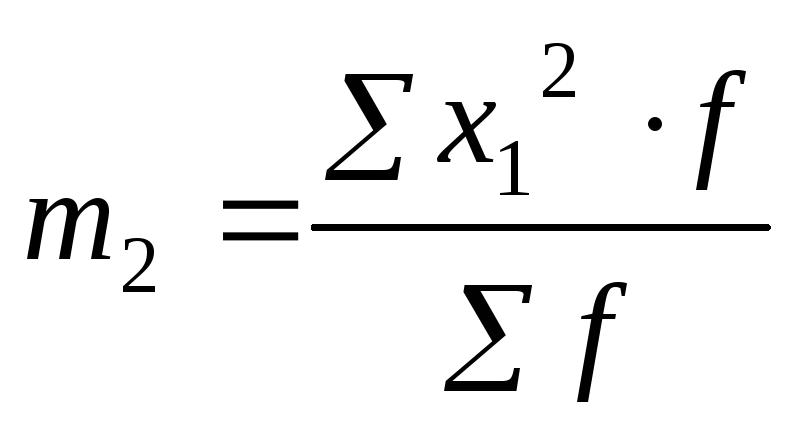 
.
Рассмотрим применение «способа моментов» в расчете дисперсии и среднеквадратического отклонения на примере следующих данных.
Пример 2. Расчет дисперсии и среднего квадратического отклонения необходимо провести по данным условия предыдущей задачи. Расчеты следует оформить в табл. 20.
Группировка работающих по возрасту, лет (х)
Удельный вес работающих, % ( f )
Середина интервала (х)
Размер интервала i = 10, А = 35 (варианта с наибольшей частотой):
;
;
;
лет.
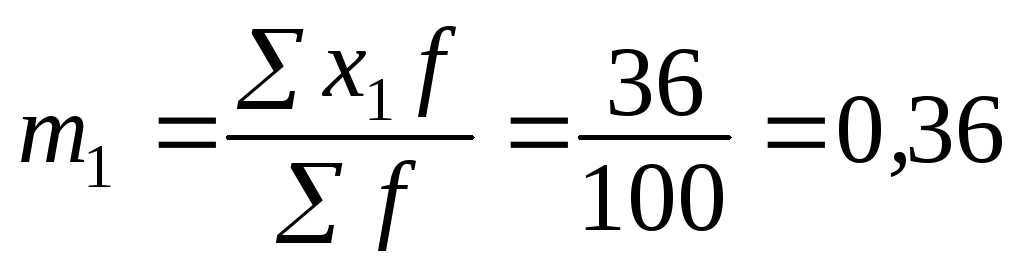
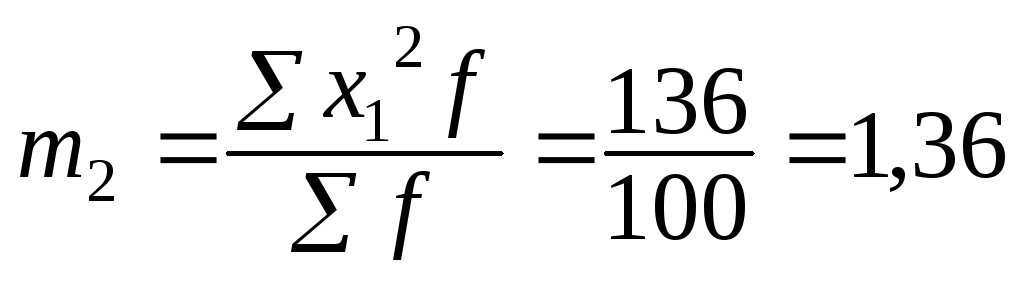
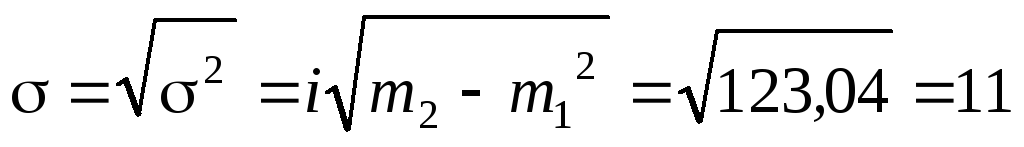
Признаки, которыми обладают одни единицы совокупности и не обладают другие, называются альтернативными. Вариацию качественных признаков можно определить, рассчитав дисперсию альтернативного признака (дисперсию доли) по формуле
,
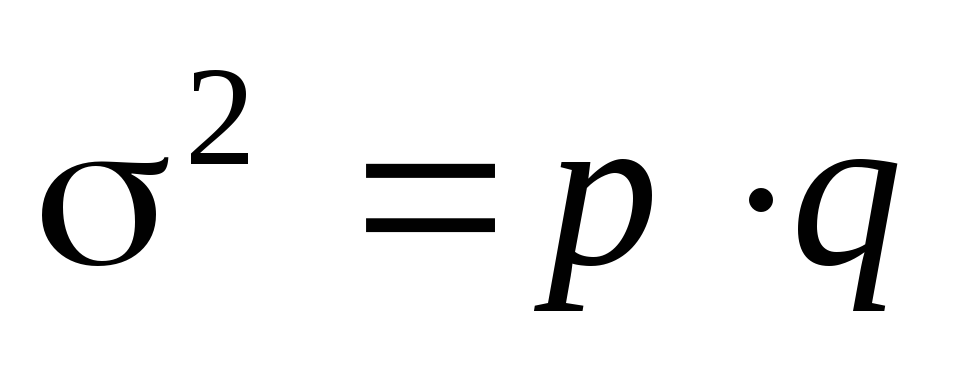
где р – доля единиц, обладающих изучаемым признаком;
q– доля единиц, не обладающих этим признаком.
В связи с тем, что p + q = 1, то q = 1 – p, следовательно,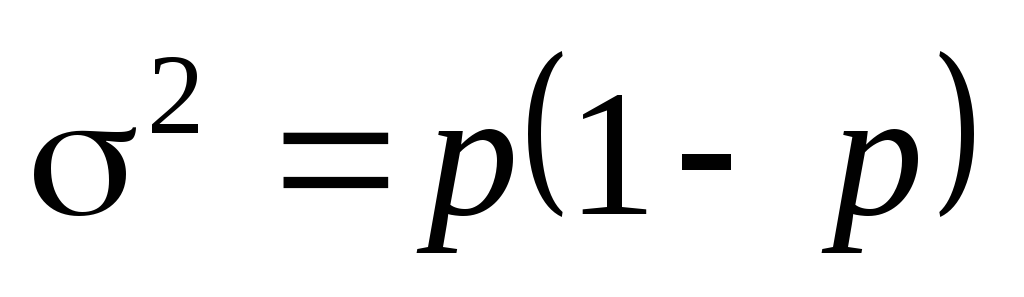 
.
Определим вариацию качественного признака в следующем примере.
Пример 3. Имеются следующие данные по Республике Беларусь (на конец 1998 г.): всего заняты в народном хозяйстве – 4416,6 тыс. чел., из них имеют высшее образование – 870,1 тыс. чел.
Необходимо определить дисперсию и среднее квадратическое отклонение доли занятых в народном хозяйстве и имеющих высшее образование.
Рассчитаем дисперсию альтернативного признака по формуле
,
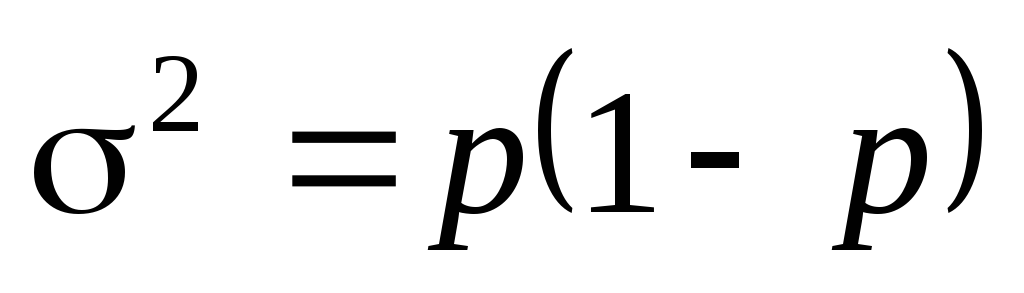
где р – доля единиц, обладающих интересующим нас признаком.
Произведем следующие расчеты:
;
;
.
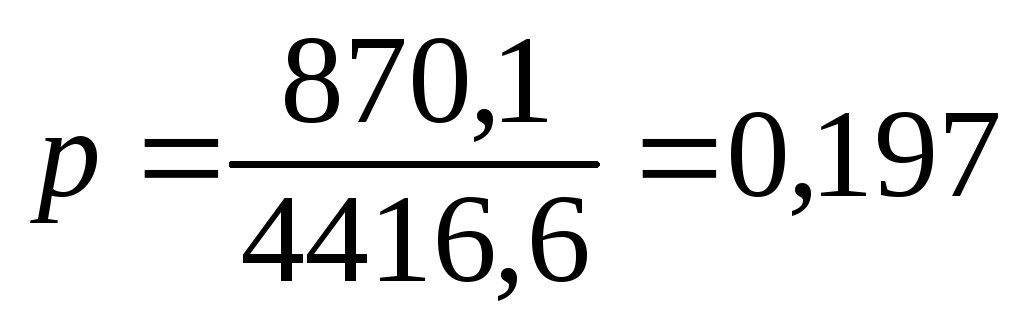
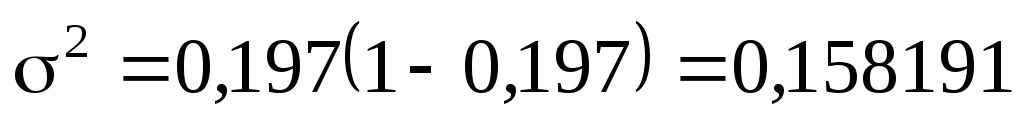
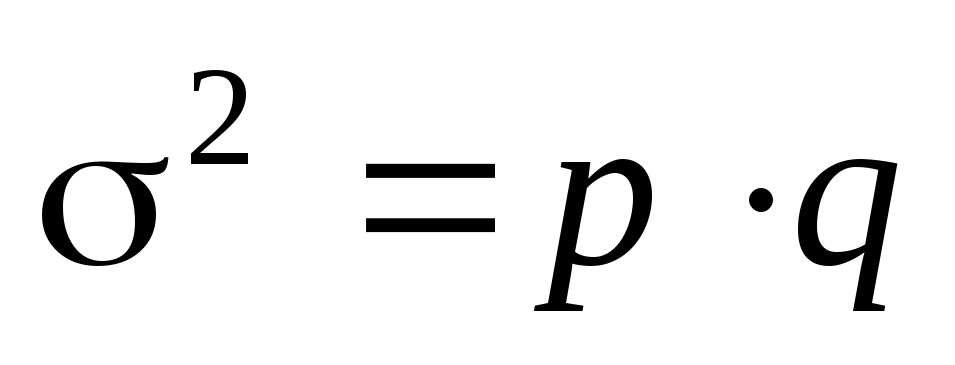
Исчислим среднее квадратическое отклонение следующим образом:
.
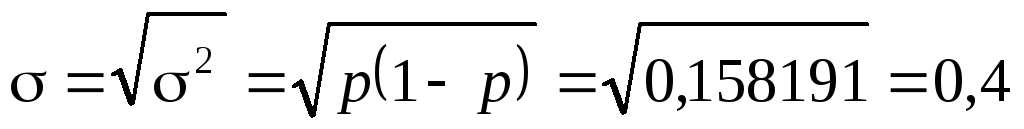
6.3. Внутригрупповая и межгрупповая вариации
Вариация признака определяется различными факторами.
Вариация, обусловленная влиянием фактора, положенного в основу группировки, называется межгрупповой вариацией и характеризуется межгрупповой дисперсией ( 2 ).
Межгрупповая дисперсия является мерой колеблемости частных (групповых) средних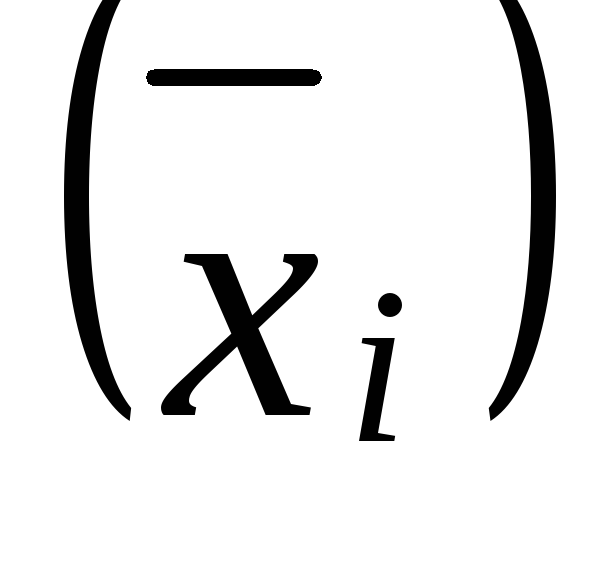 
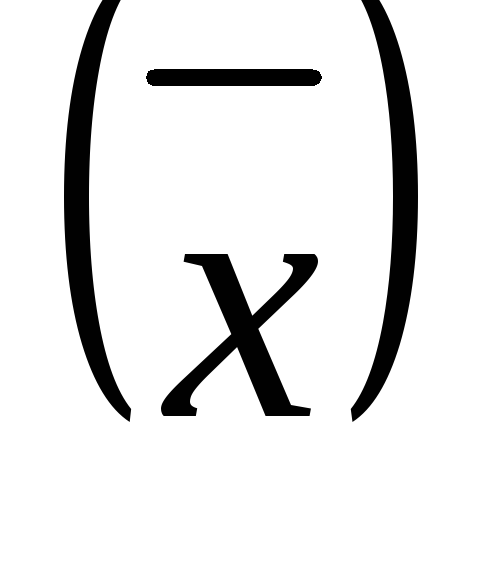
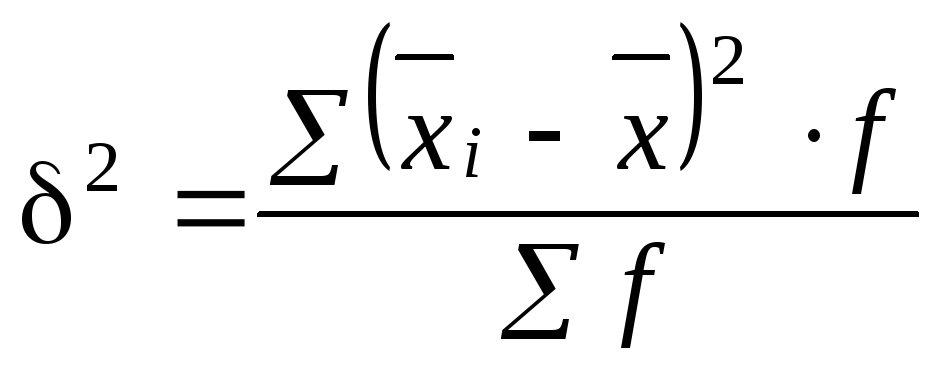
около общей средней 
и исчисляется по формуле
,
где f – количество единиц совокупности в каждой i-й группе.
Вариацию, обусловленную влиянием прочих факторов, характеризует в каждой группе внутригрупповая дисперсия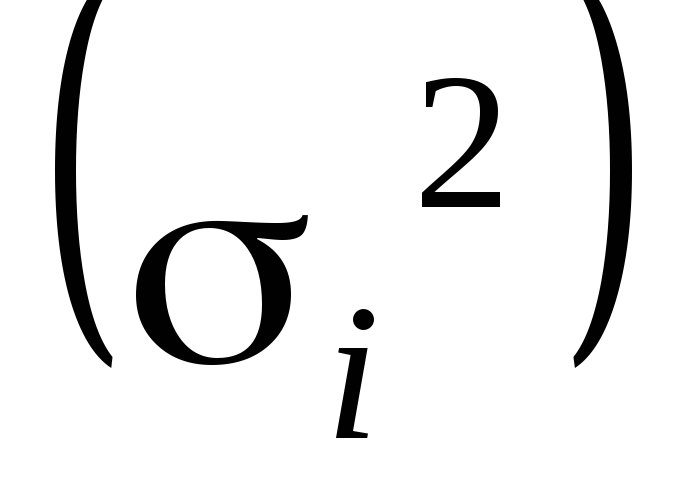 
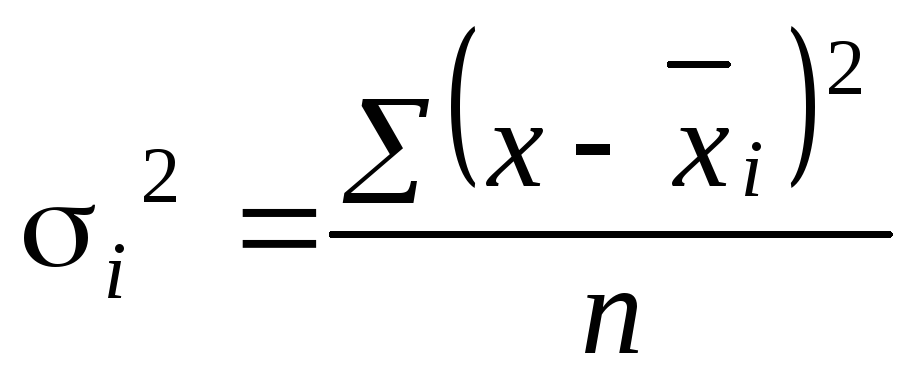
, которую определяют по следующей формуле:
.
Средняя из внутригрупповых, или частных дисперсий определяется по формуле средней арифметической взвешенной дисперсий групп
.
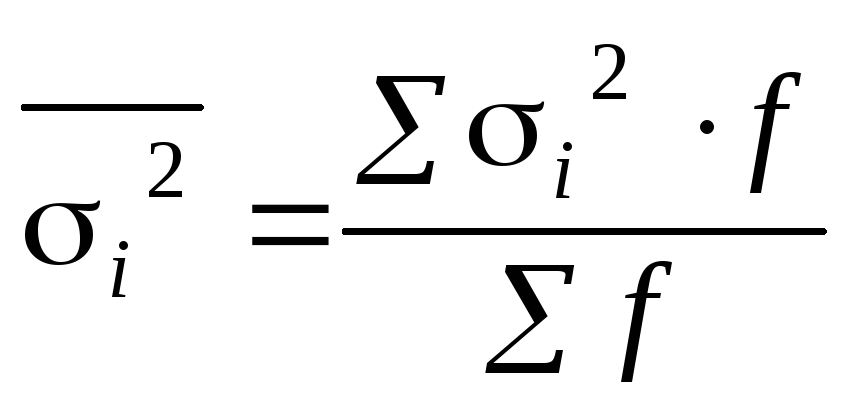
Общая дисперсия признака равна сумме межгрупповой и средней арифметической внутригрупповых дисперсий:
.
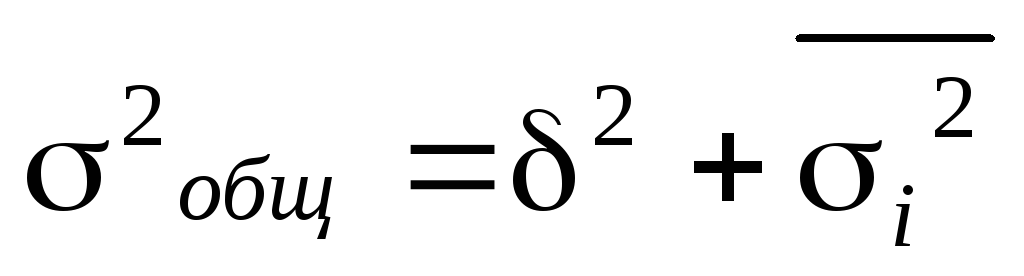
Отношение межгрупповой дисперсии к общей дает коэффициент детерминации ( 2 ). Данный коэффициент характеризует, какая доля всей вариации признака обусловлена признаком, положенным в основание группировки:
.
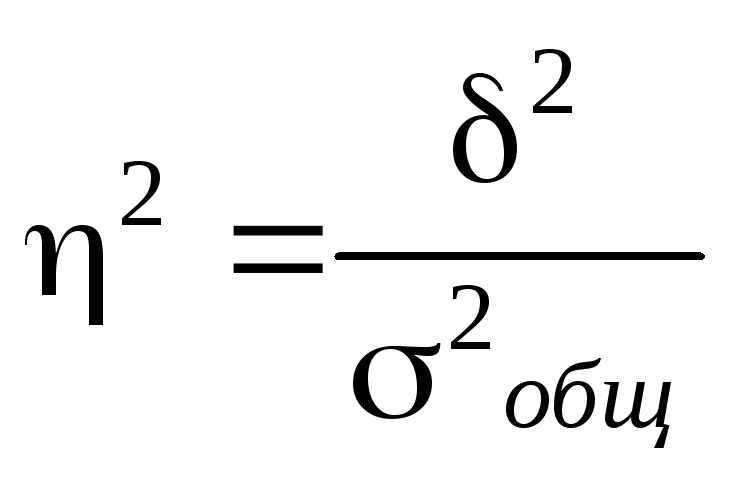
Корень квадратный из коэффициента детерминации дает эмпирическое корреляционное отношение, которое характеризует тесноту связи между группировочным и результативным признаками:
.
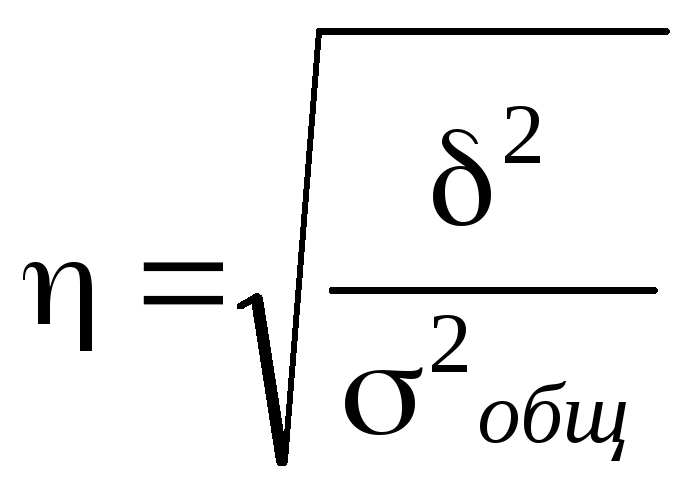
Этот показатель изменяется от 0 до 1.
Определим перечисленные выше показатели.
Пример 4. Расчеты σ 2 общ необходимо провести по данным примера 1, рассматриваемого в теме 3 (см. сводную групповую табл. 3).
Расчет межгрупповой дисперсии следует произвести по формуле
.
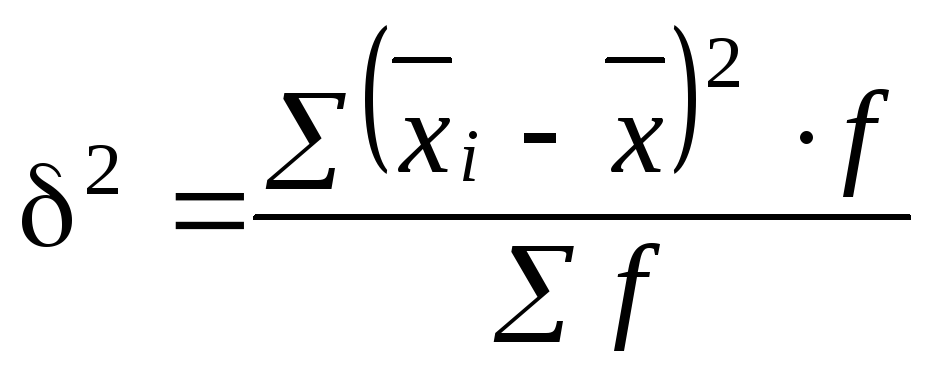
Вспомогательные расчеты необходимо оформить в табл. 21.
Источник
